Abstract
The fault diagnosis of rotating machinery has crucial significance for the safety of modern industry, and the fault feature extraction is the key link of the diagnosis process. As an effective time-frequency method, Empirical Mode Decomposition (EMD) has been widely used in signal processing and feature extraction. However, the mode mixing phenomenon may lead to confusion in the identification of multi frequency signals and restricts the applications of EMD. In this paper, a novel method based on Multi-Differential Empirical Mode Decomposition (MDEMD) was proposed to extract the energy distribution characteristics of fault signals. Firstly, multi-order differential signals were deduced and decomposed by EMD. Then, their energy distribution characteristics were extracted and utilized to construct the feature matrix. Finally, taking the feature matrix as input, the classifiers were applied to diagnosis the existence and severity of rotating machinery faults. Simulative and practical experiments were implemented respectively, and the results demonstrated that the proposed method, i.e. MDEMD, is able to eliminate the mode mixing effectively, and the feature matrix extracted by MDEMD has high separability and universality, furthermore, the fault diagnosis based on MDEMD can be accomplished more effectively and efficiently with satisfactory accuracy.
1. Introduction
Large rotating machinery is the essential part of many industrial applications, and the requirement of its safe and uninterrupted operation has become more significant. It is obvious that there is an increasing demand for reliable failure detection and fault diagnosis [1]. Several condition monitoring techniques such as vibration, acoustic and temperature measurements have been investigated for fault feature extraction, and among these techniques vibration measurement and analysis are paid more attention [2-5]. When faults of rotating machinery occur, the vibration signals will present an amplitude modulation phenomenon combining the characteristic frequencies of different defects highly correlative with the structure dynamics, thus, the vibration analysis and feature extraction have great importance for rotating machinery fault diagnosis.
In previous studies, many signal processing methods had been developed to mining the fault characteristic information, such as time-domain analysis, frequency-domain analysis, wavelet transform and empirical mode decomposition. Classical time or frequency domain methods, including the time-domain averaging [6], time-series analysis [7] and frequency spectral analysis [8], were proved to be effective for stationary vibration signals. However, as the vibration signal usually presents non-stationary characteristics in time-domain and diverts energy to a wide spectrum in frequency-domain, these traditional methods cannot sufficiently extract the diagnostic information. Wavelet transform (WT) is a powerful time-frequency method for non-stationary signal analysis by describing the signals on multiple scales with different time-frequency resolution, and it has been widely employed to investigate many kinds of signals [9-12]. The wavelet bases and the decomposition scales are determined in WT, and the frequency components of the decomposition results are only related to the sample frequency, which makes the precision of WT highly influenced by the wavelet selection and restricts its application [13].
Empirical mode decomposition (EMD) is another time-frequency signal processing technique, but different from WT, EMD is a self-adaptive method, which can decompose a non-stationary signal into a series of intrinsic mode functions (IMFs) based on the local characteristics of the signal [14]. In recent years, EMD has been becoming a research focus in signal processing and fault diagnosis [15-25]. Many researchers applied EMD and Hilbert spectrum in the mechanical faults diagnosis and achieved good results [15-18]. A combination of EMD with other signal processing techniques, such as envelope analysis, kernel independent component analysis (KICA), instantaneous dimensionless frequency (DLF) normalization and autoregressive (AR) model, also showed merit in vibration signal processing and feature extraction [19-22]. Meanwhile, according to the specific problems in different application areas, plenty kinds of promotions and modifications including boundary extension, ensemble empirical mode decomposition (EEMD), Multivariate EMD, etc, are proposed to improve the performance of EMD and extended its applications [23-25] vastly.
But unfortunately, the mode mixing phenomena of EMD caused by the signal intermittency and noise disturbance is still one major drawback [26], which may lead to confusion in the extracted features of different faults. To eliminate this defect, in this paper we proposed a feature extraction process based on multi-differential empirical mode decomposition (MDEMD), which employed the EMD to not only the original signal, but also its multi-differential signals, and extracted the energy distribution as the signal characteristics and fault features from the obtained IMFs. As the energy distribution of different frequency components would vary under differential operations, the MDEMD could obtain the fault features with high separability and eliminate the mode mixing phenomena indirectly. To verify the superiority of the proposed method MDEMD, simulative and practical experiments were implemented respectively, and taking the extracted features as input vectors several common classifiers were utilized to process the fault diagnosis.
The rest of the paper is organized as follows: In Section 2, the proposed method multi-differential empirical mode decomposition (MDEMD) is detailed described after the introduction of EMD and energy distribution extraction. In Section 3, simulation experiments are carried out and the effectiveness of MDEMD is verified. In Section 4, MDEMD is applied into the fault diagnosis for rotating machinery, and the results and discussion are given. Section 5 summarizes the conclusions of this work.
2. Multi-differential empirical mode decomposition
2.1. Empirical mode decomposition
EMD is a newly self-adaptive time-frequency technique for non-linear and non-stationary signal processing, which is able to decompose a complex multicomponent signal into a set of intrinsic mode functions (IMFs) satisfying the following two requirements: (1) In the whole set data, the number of extremum and the number of zero-crossings must either be equal or different at most by one; (2) At any point, the mean of the envelope defined by local maxima and the envelope defined by the local minima are zero [14]. Suppose a signal as and its decomposition procedure is described as follows.
Step 1: Set the original signal , and initialize the iteration tag ;
Step 2: Find all the local maxima and minima of .
Step 3: Construct the upper envelope and lower envelope respectively from the extracted local maxima and minima via the cubic spline curve fitting.
Step 4: Compute the local mean , and subtract from the original signal to obtain the first component .
Step 5: Set the new , repeat Step 2 to 4 until meets the requirement of IMF, then design as the th IMF.
Step 6: Subtract from to obtain the new , if the new satisfies the stopping criteria, design as the residue of the signal and stop decomposition process; otherwise, set , and repeat from Step 2.
After the decomposition procedure, the investigated signal can be expressed as follows:
where is the amount of IMFs, is the th IMF, and is the residue.
2.2. Energy distribution extraction
As mentioned before, the non-stationary vibration signal usually contains a wide spectrum of frequency components, which could be decomposed into a sequence of IMFs with different frequency scales self-adaptably by EMD. Theoretically, the decomposition result is only related to the inherent characteristics of the signal itself, and each IMF contains a different band of frequency components. Through the analysis of IMFs, the implied characteristic information can be revealed, and in this paper, energy distribution is extracted as the signal features.
The energy distribution obtained by estimating the total energy of the signal and energy percentage of each IMF is able to present the frequency construction of the signal. To extract the energy distribution, firstly, the energy of each IMF is computed:
Then, the energy percentage can be evaluated:
Finally, the total energy of all the IMFs defined as is combined with the energy percentage to construct the feature vector . It can be noticed that the extracted feature vector is able to represent the characteristics of a signal in both macroscopic (total energy ) and microscopic (energy percentage ) ways. Usually, when different signals are investigated, the amount of obtained IMFs can hardly be the same, and a certain number of the chosen IMFs should be decided. In previous studies, it is found out that the most energy of the signal are contained in the first few IMFs, therefore, for single signal analysis, the number is chosen if the sum energy percentage of the first IMFs is larger than 95 %, and for multi signals analysis, the largest is utilized for all the signals, and the feature vector can be expressed as . Particularly, when the amount of IMFs is smaller than , 0 is assigned to the rest of the vectors.
2.3. Multi-differential EMD and feature extraction
The feature extraction process based on EMD and energy distribution is applicable to signal identification and fault diagnosis, however, its effectiveness is restricted by the mode mixing of EMD. To illustrate this pheromone, a simple example is shown below.
Define two different signals and as follows:
Obviously, has more frequency components than , and they are easy to distinguish. Utilize EMD and energy distribution extraction to analyze these two signals, and the IMFs and feature vector are respectively listed in Fig. 1 and Table 1. It can be noticed that is decomposed into two IMFs: the first one is the higher frequency component, and the other one is the main component, which means the two different frequency components implied in can be separated from each other quite well by EMD. On the other hand, is also decomposed into two IMFs, but the first two components of are both contained in IMF2, which suggests the signal cannot be decomposed sufficiently by EMD. The undesirable consequence of the mode mixing pheromone is revealed in Table 1, from which it can be seen that the extracted feature vectors of and based on EMD are nearly the same, and obviously, the two different signals cannot be identified by these feature vectors.
Table 1The extracted feature vectors of the signal x1 and x2
Signal | Features | ||
1.50×103 | 0.0025 | 0.9975 | |
1.56×103 | 0.0024 | 0.9976 | |
Fig. 1The EMD result of the signal (a) x1 and (b) x2
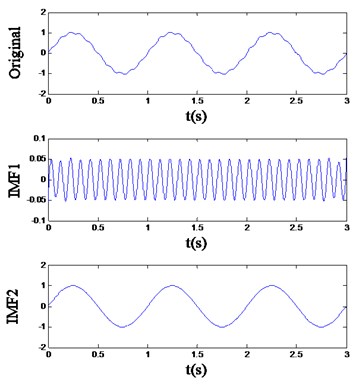
(a)
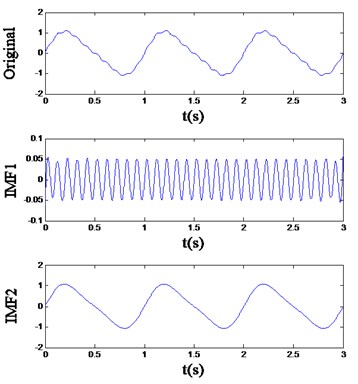
(b)
The most fundamental reason causing the mode mixing is the local extremum selection. One major procedure during the EMD process is calculating the upper and lower envelopes based on the local extremum, and it can be noticed that the amount and the location of the local extremum decides the main frequency components of the current IMF directly. Whether two components can be separated depends on the information of the local extremum. When the frequencies of two components are close, or the amplitude of the higher frequency component is low, the higher frequency component may not generate the local extremum reflecting the real frequency distribution and is hardly to decompose. As is shown in Fig. 1(b), IMF2 contains two components and with close frequencies 1 and 2 Hz, and the amplitude of is much lower, thus only influences the location of the local extremum, but cannot generate new local extremum, and they haven’t been separated.
To eliminate the mode mixing, differential algorithm is introduced into EMD. Theoretically, the differential signal has such properties: (1) it won’t change the frequencies of all the components; (2) it will increase the amplitude of component according to its frequency. It is noteworthy that the amplitude increase is linearly related to the frequency of the component, and according to the previous discussions, such properties are very helpful for improving the EMD. The higher frequency component with low amplitude will be strengthened in the differential signal, and may be able to generate new local extremum. The example above is utilized again to demonstrate the effectiveness of the differential EMD. First, the differential signals of and are calculated by central difference as follows:
where presents a small increments of , and then, the feature extraction process is carried out with the differential signals.
The result is shown in Fig. 2 and Table 2. Although an undesirable fake IMF appears in Fig. 2(b), the actual components implied in the differential signal of are decomposed into three IMFs effectively, and extracted feature vectors listed in Table 2 can be noticed to have high separability. Additionally, when the EMD result of the 1st-order differential signal still cannot separate the different frequency components, the 2nd-order and higher-order differential signals could be utilized:
Fig. 2The differential EMD result of the signal (a) x1 and (b) x2
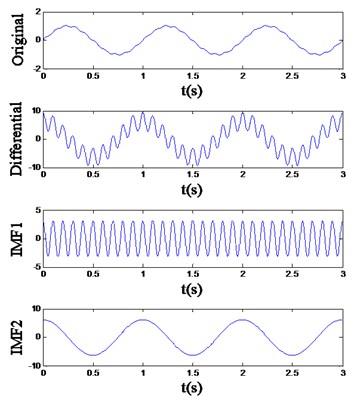
a)
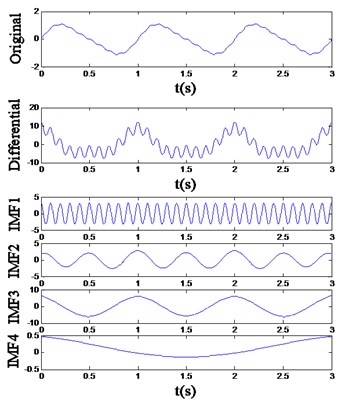
b)
Table 2The extracted feature vectors of the signal x1 and x2 by differential EMD
Signal | Features | ||||
EP1 | EP2 | EP3 | EP4 | ||
6.10×104 | 0.2000 | 0.8000 | 0.0000 | 0.0000 | |
5.53×104 | 0.1939 | 0.1150 | 0.6688 | 0.0023 | |
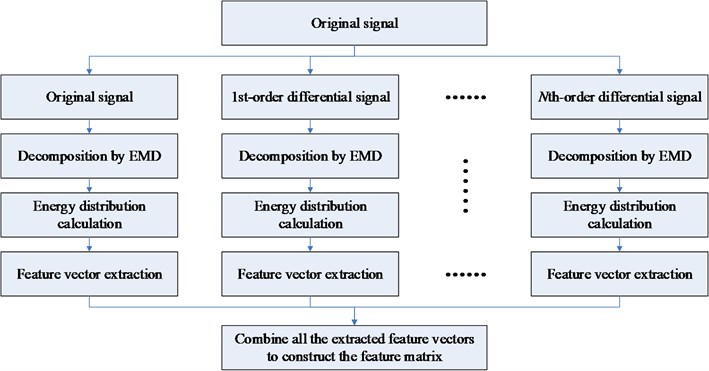
Based on the above studies, a novel Multi-Differential EMD (MDEMD) method is proposed to improve the effectiveness of the signal decomposition and feature extraction by combining the energy distribution characteristics of multi-order differential signals, and the flow chart of MDEMD is shown in Fig. 3. Multi-order differential signals are obtained, and the energy distribution features of these signals are extracted respectively. To represent the signal more comprehensively, all the extracted feature vectors are combined to construct the feature matrix. During the MDEMD process, the higher order is chosen, the more frequency information could be obtained, but the high order differential operation may lead to serious signal distortion. Therefore, the max order of multi-order differential signal should be decided by the complexity of the investigated signal.
Fig. 3The flow chart of MDEMD
3. Simulation experiment
3.1. Simulation signals
In this section, artificial signals are constructed to simulate the vibration signals of rotating machinery, and the simulation experiment is implemented to verify the superiority of the proposed MDEMD method. A set of signal components are defined in Eq. 4, and a certain combination of them can simulate the vibration response of the corresponding fault [18].
where is a sinusoidal signal with the frequency of 60 Hz representing the 1 component, is an intra-wave modulated signal representing the harmonic component, and are both sinusoidal signals representing the and harmonic components, and is the noise signal. Previous researches have found that the vibration is often caused by mass unbalance, and the excitation source of vibration harmonic is usually misalignment, while the and vibration harmonic components constantly appear in the response of rubbing fault. In the simulation experiment, four classes of signals with different combinations of are established as follows:
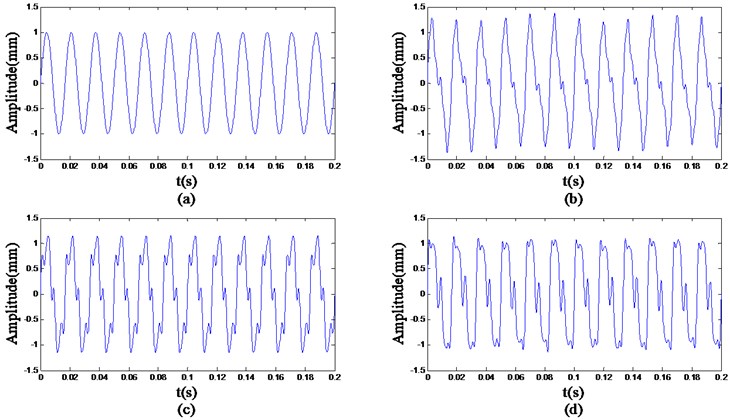
where is a random number in the range of [0.3, 0.4], is a random number in the range of [0.28, 0.32], and is a random number in the range of [0.09, 0.11]. Forty samples for each class are produced with different ,, , 25 of which are training samples and the other are testing samples. Fig. 4 gives a set of examples of the four classes.
Fig. 4Examples of the four classes: (a) x1, (b) x2, (c) x3 and (d) x4
3.2. Signal decomposing and feature extraction analysis
In the simulation experiment, the max-order of MDEMD is set to 2, and EMD is applied to the original and multi-order differential signals. As the amplitude of signal would change after the differential operation, in order to make the extracted energy distribution more convincing, the differential signal is divided by a determined factor equals to 120π, so that the amplitude of component would keep invariant. The main IMFs obtained by EMD of the example signals are respectively shown in Fig. 5 to 7.
Fig. 5The decomposition result of the original signals
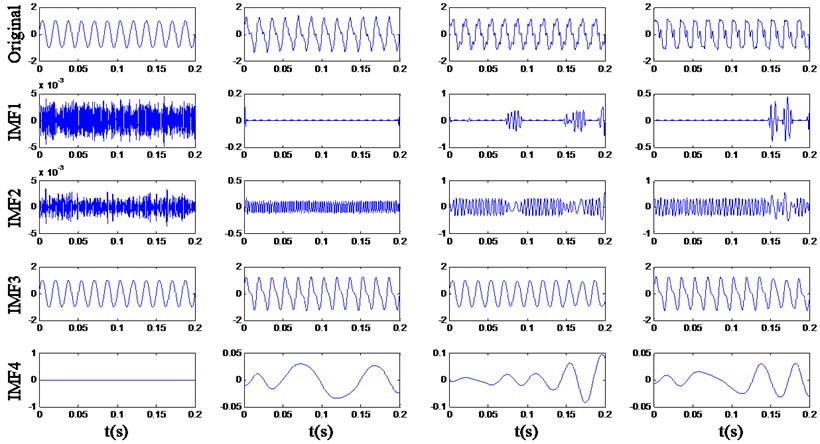
Fig. 6The decomposition result of the 1-order differential signals (1-ODS)
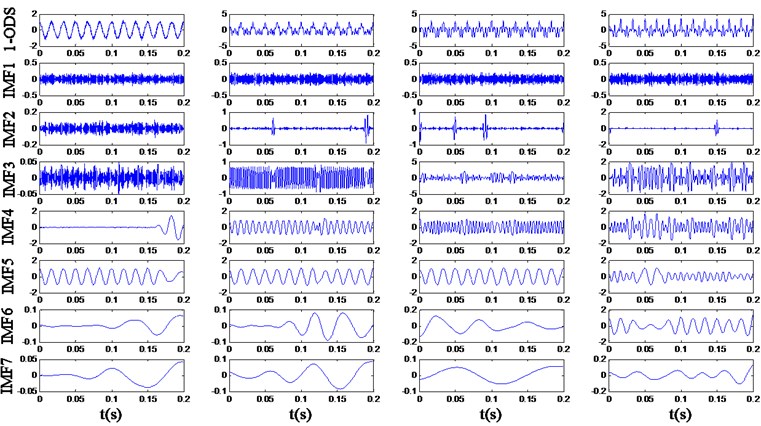
Fig. 7The decomposition result of the 2-order differential signals (2-ODS)
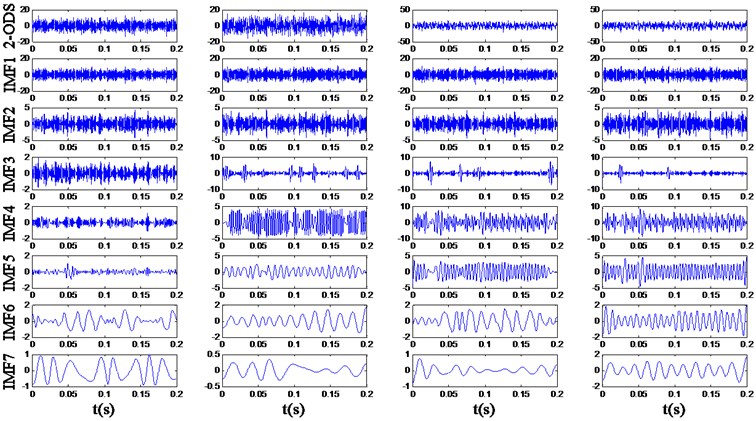
In Fig. 5 it is revealed that multiple frequency components contained in the simulation samples cannot be decomposed sufficiently by EMD and the mode mixing exists evidently. For example, the IMF3 of signal and contains and components, and the IMF2 of contains 4 and harmonic components. In Fig. 6 and 7, the amplitude of higher frequency components rises more obviously through the differential process, and the influence of noise signals becomes more serious. However, although the smoothness of the signals decreases, the multiple frequency components implied in the multi-order differential signals can be decomposed more sufficiently.
Based on decomposition results, the feature matrixes of energy distribution are extracted and parts of them are listed in Table 3. Through comparison of the feature vectors extracted from multi-order differential signals, it is revealed that the energy distributions of four original signals are quite similar to each other, while the energy distributions of 1- and 2-order differential signals have quite big differences.
Table 3The extracted feature matrixes of the four examples
Signal | Features matrix | |||||||||
Original | 1.00×103 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
1-ODS | 9.47×102 | 0.010 | 0.002 | 0.001 | 0.222 | 0.761 | 0.001 | 0.001 | 0.000 | |
2-ODS | 2.81×104 | 0.838 | 0.093 | 0.018 | 0.006 | 0.003 | 0.023 | 0.017 | 0.001 | |
Original | 1.17×103 | 0.000 | 0.010 | 0.987 | 0.001 | 0.001 | 0.001 | 0.000 | 0.000 | |
1-ODS | 1.18×103 | 0.008 | 0.012 | 0.206 | 0.334 | 0.436 | 0.002 | 0.002 | 0.000 | |
2-ODS | 3.68×104 | 0.598 | 0.063 | 0.083 | 0.189 | 0.049 | 0.017 | 0.001 | 0.000 | |
Original | 9.84×102 | 0.027 | 0.080 | 0.890 | 0.002 | 0.000 | 0.000 | 0.001 | 0.000 | |
1-ODS | 1.52×103 | 0.005 | 0.015 | 0.372 | 0.224 | 0.377 | 0.003 | 0.001 | 0.003 | |
2-ODS | 3.79×104 | 0.486 | 0.048 | 0.066 | 0.292 | 0.088 | 0.017 | 0.002 | 0.001 | |
Original | 1.17×103 | 0.009 | 0.080 | 0.907 | 0.001 | 0.002 | 0.001 | 0.000 | 0.000 | |
1-ODS | 1.96×103 | 0.005 | 0.008 | 0.393 | 0.279 | 0.107 | 0.204 | 0.001 | 0.003 | |
2-ODS | 4.10×104 | 0.506 | 0.062 | 0.025 | 0.273 | 0.100 | 0.019 | 0.013 | 0.002 | |
To verify the separability of the extracted features, Support Vector Machine (SVM), which is a common pattern recognition method based on the structural risk minimization (SRM) principle [27], is applied to identify the four classes of simulation signals with the energy distribution characteristics respectively obtained by the original EMD, 1- and 2-order MDEMD. The identification results are summarized in Table 4. By the original EMD method, the identification rates of the four classes are quite different and the average identification rates of training and testing samples are respectively 67.7 and 65.3 %, which are too low for the signal identification. By the 1-order MDEMD, all the identification rates are significantly improved, and the average identification rates rise to 93.9 and 94.2 %. By the 2-order MDEMD, the accuracy is further improved, and the identification rates of three classes have reached 100 %. The simulation experimental result verifies the separebility of the extracted features and demonstrates that the proposed MDEMD method is suitable for signal identification.
Table 4The identification results
Class of signals | Accuracy of EMD | Accuracy of 1-order MDEMD | Accuracy of 2-order MDEMD | |||
Training | Testing | Training | Testing | Training | Testing | |
48.0 % | 50.6 % | 86.4 % | 85.3 % | 100 % | 100 % | |
82.4 % | 82.0 % | 100 % | 100 % | 100 % | 100 % | |
80.0 % | 72.0 % | 89.2 % | 91.3 % | 92.4 % | 92.0 % | |
60.4 % | 56.7 % | 100 % | 100 % | 100 % | 100 % | |
Average | 67.7 % | 65.3 % | 93.9 % | 94.2 % | 98.1 % | 98.0 % |
4. Applications in fault diagnosis for rotating machinery
4.1. Data collection
Rolling element bearings are the major part of most rotating machineries, and detecting and diagnosing the existence and severity of bearing faults is significant to prevent the rotating mechanical system from fatal breakdowns. In this section, the proposed MDEMD method is applied to feature extraction and fault diagnosis for rolling element bearings.
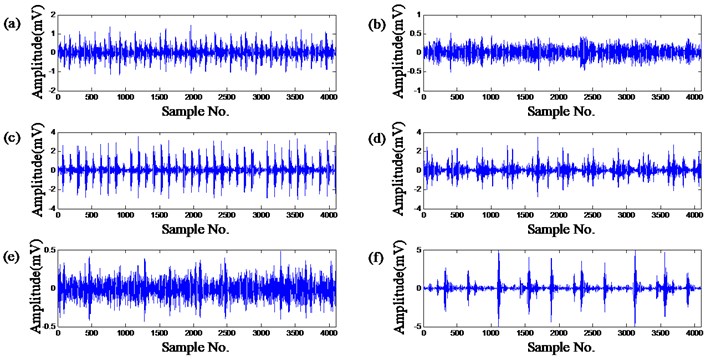
Part of the bearings vibration dataset collected by K. A. Loparo [28] is used in this paper. Three faults including outer race fault, inner race fault and ball fault, with the same defect sizes of 0.007 or 0.021 in, were respectively introduced into the drive-end bearing of the motor, which were tested under four different loads, 0, 1, 2 and 3 hp and the vibration data was collected at 12000 samples/s and 24000 samples/s by the installed sensors. In this paper, the vibration data collected at 12000 samples/s under 0 hp load with the defect sizes of 0.007 or 0.021 in was utilized and divided into 100 sub-signals with 4096 data points for each group. The produced 6 classes of samples covering 6 types of faults are listed in Table 5, and their time responses are illustrated in Fig. 8.
Table 5Description of bearing fault dataset
The number of fault samples | Defect size (in) | Position of fault | Label of class |
100 | 0.007 | Out race | |
100 | 0.007 | Inner race | |
100 | 0.007 | Ball | |
100 | 0.021 | Out race | |
100 | 0.021 | Inner race | |
100 | 0.021 | Ball |
Fig. 8Time series of fault signals: (a) ball fault with 0.007 in; (b) inner race fault with 0.007 in; (c) outer race fault with 0.007 in; (d) ball fault with 0.021 in; (e) inner race fault with 0.021 in; (f) outer race fault with 0.021 in
4.2. Feature extraction and fault diagnosis
Based on the theories above, the energy distribution characteristics of all the samples are extracted from the original and multi-order differential signals respectively, and the length of the extracted feature vectors is set to 10 containing 1 and 9 . After feature extraction, the obtained feature matrixes were scaled to be in [0, 1].
The fault diagnosis experiments were carried out with the fault features respectively extracted by the original EMD, 1- and 2-order MDEMD, and half of the samples for each class were randomly selected as training data leaving the rest as testing data. Furthermore, the four most common classifiers including k-Nearest Neighbor algorithm (kNN), Radial Basis Function (RBF) Neural Network, Support Vector Machine (SVM) and Probabilistic Neural Network (PNN) were applied to identify the 6 classes of faults, and the experiment of each method was repeated for 30 times.
Table 6 shows the comparison results of different diagnostic methods, and the identification rates of training and testing samples are reported respectively. It is clear that, the testing accuracy of 1-order MDEMD is much higher than the original EMD and reaches to more than 98.70 %, while the identification rate of 2-order MDEMD is further increased to more than 99 %. It is also noticed that the identification accuracies of different classifiers varied in a small range. The minimum testing accuracy by using original EMD is 92.11 % for RBF while the maximum is 95.68 % for PNN, and the variance is 3.57 %. By using 1-order MDEMD, the minimum and maximum testing accuracies are respectively 98.70 and 99.33 % corresponding to RBF and PNN, and the variance deduced to only 0.63 %. Especially, by utilizing 2-order MDEMD the lowest accuracy is 99.04 % for kNN, and the identification rates of SVM and PNN are nearly 100 %. Therefore the effectiveness and universality of the proposed MDEMD are demonstrated.
Table 6The fault identification rates of different methods
Method | Identification rate of training samples (%) | Identification rate of testing samples (%) | ||||
Original EMD | 1-order MDEMD | 2-order MDEMD | Original EMD | 1-order MDEMD | 2-order MDEMD | |
kNN | 95.63 | 98.76 | 99.27 | 94.47 | 98.72 | 99.04 |
RBF | 93.54 | 98.91 | 99.81 | 92.11 | 98.70 | 99.46 |
SVM | 94.93 | 99.25 | 99.95 | 94.56 | 99.03 | 99.80 |
PNN | 98.50 | 100 | 100 | 95.68 | 99.33 | 99.86 |
Meanwhile, it is noteworthy that the higher order for MDEMD would produce lager feature matrix, and the time consumption would increase accompanied with the accuracy, thus, the selection of the proper order depends on the balance between the requirements of the accuracy and efficiency. For the fault diagnosis of rotating machinery, the recommended max order is 2. In summary, the comparison results reflect that MDEMD can stably extract the fault features with high separabilities and the fault diagnosis can be completed with satisfactory accuracy by using these fault features. It is feasible for fault diagnosis of rotating machinery.
5. Conclusion
In this paper, a novel method of feature extraction based on Multi-Differential Empirical Mode Decomposition for fault diagnosis of rotating machinery was proposed and described, where the feature matrix of energy distribution is extracted from the EMD results of multi-order differential signals automatically. Simulation experiment was implemented with four classes of signals containing different frequency components, and the decomposition results and extracted features were described and discussed. Meanwhile, six classes of fault datasets for the rolling element bearings were utilized in the practical experiment, and the fault features are extracted by different order MDEMD and identified by four most common classifiers. The diagnosis results were compared with the original EMD in both training and testing identification rates. The experimental results showed that the proposed method is suitable for the feature extraction of rotating machinery, and it is an important support for realizing automatic fault diagnosis with satisfactory accuracy.
References
-
Liu T., Chen J., Dong G. M., Xiao W. B., Zhou X. N. The fault detection and diagnosis in rolling element bearings using frequency band entropy. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 227, Issue 1, 2012, p. 87-99.
-
Lee H. Sound radiation from in-plane vibration of thick annular discs with a narrow radial slot. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 227, Issue 5, 2012, p. 919-934.
-
Dong G. M., Chen J. Noise resistant time frequency analysis and application in fault diagnosis of rolling element bearings. Mechanical Systems and Signal Processing, Vol. 33, 2012, p. 212-236.
-
Castro de H. F., Cavalca K. L., Camargo de L. W. F., Bachschmid N. Identification of unbalance forces by metaheuristic search algorithms. Mechanical Systems and Signal Processing, Vol. 24, 2010, p. 1785-1798.
-
Xiang X. Q., Zhou J. Z., An X. L., Peng B., Yang J. J. Fault diagnosis based on Walsh transform and support vector machine. Mechanical Systems and Signal Processing, Vol. 22, 2008, p. 1685-1693.
-
McFadden P. D. Examination of a technique for the early detection of failure in gears by signal processing of the time domain average of the meshing vibration. Mechanical Systems and Signal Processing, Vol. 1, 1987, p. 173-183.
-
Wang C., Kang Y., Shen P., Chang Y., Chung Y. Applications of fault diagnosis in rotating machinery by using time series analysis with neural network. Expert Systems with Applications, Vol. 37, 2010, p. 1696-1702.
-
Sanza J., Pererab R., Huertab C. Fault diagnosis of rotating machinery based on auto-associative neural networks and wavelet transforms. Journal of Sound and Vibration, Vol. 302, 2007, p. 981-999.
-
Newland D. E. An introduction to random vibrations, Spectral & Wavelet Analysis. Third ed., Longman Scientific & Technical, England, 2005.
-
Zhang Y. P., Huang S. H., Hou J. H., Tao S., Wei L. Continuous wavelet grey moment approach for vibration analysis of rotating machinery. Mechanical Systems and Signal Processing, Vol. 20, 2006, p. 1202-1220.
-
Abbasion S., Rafsanjani A., Farshidianfar A., Irani N. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mechanical Systems and Signal Processing, Vol. 21, 2007, p. 2933-2945.
-
Al-Badour F., Sunar M., Cheded L. Vibration analysis of rotating machinery using time-frequency analysis and wavelet techniques. Mechanical Systems and Signal Processing, Vol. 25, 2011, p. 2083-2101.
-
Dou D. Y., Yang J. G., Liu J. T., Zhao Y. K. A rule-based intelligent method for fault diagnosis of rotating machinery. Knowledge-Based Systems, Vol. 36, 2012, p. 1-8.
-
Huang N. E., Shen Z., Long S. R. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis. Proc. R. Soc. Lond., Vol. 454, 1998, p. 903-995.
-
Liu B., Riemenschneider S., Xu Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum. Mechanical Systems and Signal Processing, Vol. 20, Issue 3, 2006, p. 718-734.
-
Qin Y., Qin S. R., Mao Y. F. Research on iterated Hilbert transform and its application in mechanical fault diagnosis. Mechanical Systems and Signal Processing, Vol. 22, Issue 8, 2008, p. 1967-1980.
-
Yang Y., He Y. G., Cheng J. S., Yu D. J. A gear fault diagnosis using Hilbert spectrum based on MODWPT and a comparison with EMD approach. Measurement, Vol. 42, Issue 4, 2009, p. 542-551.
-
Xiong X., Yang S. X., Gan C. B. A new procedure for extracting fault feature of multi-frequency signal from rotating machinery. Mechanical Systems and Signal Processing, Vol. 32, 2012, p. 306-319.
-
Tsao W. C., Li Y. F., Le D. D., Pan M. C. An insight concept to select appropriate IMFs for envelope analysis of bearing fault diagnosis. Measurement, Vol. 45, 2012, p. 1489-1498.
-
Li Z. X., Yan X. P., Tian Z., Yuan C. Q., Peng Z. X., Li L. Blind vibration component separation and nonlinear feature extraction applied to the nonstationary vibration signals for the gearbox multi-fault diagnosis. Measurement, Vol. 46, 2013, p. 259-271.
-
Wu T. Y., Chen J. C., Wang C. C. Characterization of gear faults in variable rotating speed using Hilbert-Huang Transform and instantaneous dimensionless frequency normalization. Mechanical Systems and Signal Processing, Vol. 30, 2012, p. 103-122.
-
Wang Y. J., Kang S. Q., Jiang Y. C., Yang G. X., Song L. X., Mikulovich V. I. Classification of fault location and the degree of performance degradation of a rolling bearing based on an improved hyper-sphere-structured multi-class support vector machine. Mechanical Systems and Signal Processing, Vol. 29, 2012, p. 404-414.
-
Parey A., Pachori R. B. Variable cosine windowing of intrinsic mode functions: Application to gear fault diagnosis. Measurement, Vol. 45, 2012, p. 415-426.
-
Wu Z. H., Huang N. E. Ensemble empirical mode decomposition: a noise assisted data analysis method. Adv. Adapt. Data Analysis, Vol. 1, 2009, p. 1-41.
-
Zhao X. M., Patel T. H., Zuo M. J. Multivariate EMD and full spectrum based condition monitoring for rotating machinery. Mechanical Systems and Signal Processing, Vol. 27, 2012, p. 712-728.
-
Bao F., Wang X. L., Tao Z. Y. EMD-based extraction of modulated cavitation noise. Mechanical Systems and Signal Processing, Vol. 24, 2010, p. 2124-2136.
-
Vapnik V. N. The Nature of Statistical Learning Theory. Springer-Verlag, New York, 1999.
-
Loparo K. A. Bearings vibration dataset. Case Western Reserve University, 2011, http://www.eecs.case.edu/laboratory/bearing/download.htm.
About this article
The work described in this paper is supported by the National Natural Science Foundation of China under Grant No. 51239004, the National Natural Science Foundation of China under Grant No. 51079057, and the Research Funds of University and College PhD Discipline of China (No. 20100142110012).
