Abstract
To design the similitude test model having the same nature characteristics with the prototype of the elastic thin plates, an innovative method of confirm the structure size applicable interval of distorted (incomplete geometrically) similar model was proposed. Firstly, the complete scaling laws and the distortion scaling laws between the model and its prototype were established by using the governing equation analysis. Then, under the study of the structure size applicable interval which kept the same first-order nature characteristic (nature frequency and vibration mode), through the research of the vibration mode control interval (each order of the mode keep the same) and the predict interval of frequency, the method of structure size applicable interval of distorted similar model was obtained, which they were in different orders with the same nature characteristic. Finally, the proposed calculation method is verified by experiment.
1. Introduction
Elastic thin plate is a common component in engineering, generally the plate whose minimum width is 5-80 times than its thickness is called thin plate [1], which can bear plane tension and bending moments, it has been widely used in aeronautics, ship, ocean platform and other engineering field. Vibration analysis is one of the important research contents in the dynamic analysis of thin plate construction, for example, the thin plate construction used in engine, ship and ocean platform will be greatly destroyed by severe vibration which is produced by the effect of airflow or ocean waves [2, 3], however, the experimental evaluation of the prototypes is costly and time consuming because of the large volume, complexity, and high production cost, etc. Consequently, a dynamic scaled down model is necessary. The scaling laws of complete geometric similarity is rarely used in designing a similar model because of the complexity and size parameter limitations of the prototype structures, for example, for some thin plate structure, if the thickness is scaled down in the same ratio with its length and width, ,the structure will be too thin to process. So the incomplete geometric similar model, namely distorted model, is more widely used. However, not all distorted models can be used to predict the vibration characteristics of the prototype, especially for nature characteristic test, it is a basic requirement that there are the proportional nature frequencies and the same mode shapes between the model and the prototype.
Test models of plate structure have been studied extensively by many researchers. Li Shirong [4] studied the similitude transformation between the functionally graded and homogenous circular plates by axisymmetric bending, bucking and free vibration solutions based on the classical plate theory. Zhang Zhenhua [5] studied distorted similitude of dynamic response of the clamped and stiffened plate under uniform impact load, and established modified model that can predict impact response of the prototype. Ungbhakorn [6] established the scaling laws of distorted models by governing equations, and studied prediction accuracy of the scaling laws under the conditions of different distortion. Simitses [7] established the scaling laws of distorted models by applying the solution of critical load and nature frequency of laminated plates, and analyzed the distorted model prediction discrepancy of different materials. Rezaeepazhand [8] explained the importance of the range of distorted model similarity through applying scaled-down models for predicting vibration response of laminated plates. To sum up, it is rare that studying design methods and geometric intervals of distorted models for high order nature characteristic prediction of plates.
In this paper, by governing equation, establishing the scaling laws between the model and the prototype, and analyzing structure size factors of nature characteristic prediction discrepancy of simply supported plates and mode shape control intervals of that. A general determination method of the structure size intervals of distorted model tests of the elastic thin plates was studied, which can remain the same nature characteristics of different order between the model and the prototype.
2. Establishment of scaling laws and discrepancy analysis
2.1. Establishment of scaling laws of the four-side simply supported elastic plate
The simply supported elastic thin plate is shown in Fig. 1. In the figure, is the length, is the width, is the thickness, is the Young's modulus, is the Poisson's ratio and , are the bending moments.
Fig. 1Simply supported plate
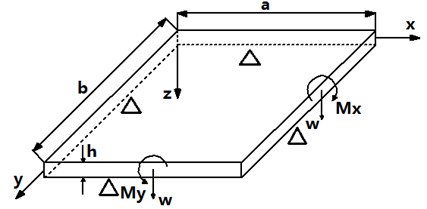
According to the Kirchhoff’s assumption, the governing equation of the thin plate can be written as [9]:
where, , is the mass area ratio, is the deflection, is the Laplace operator, .
For the four-side simply supported plate, the boundary conditions of the Hoff theory are:
Set vibration mode function of each point as , the deflection of the plate is defined as:
Substitute Eq. (4) into Eq. (1), then the free vibration characteristics are governed by:
The scaling factor is defined as , where, is the symbol of physical quantities, such as etc. Assuming that the model and prototype have the same materials, then the governing equations of the model and prototype can be written as:
Eq. (6) can be written as:
Compared with Eq. (7), for the equal corresponding parameters of the equations, the following relationship can be achieved:
According to , the following relationship can be obtained:
Substitute Eq. (10) into Eq. (9), then complete geometric similarity scaling laws of the nature frequency of the four-side simply supported elastic plates are simplified as:
For incomplete geometric similar models, , then , so the new scaling laws must be established. It is assumed that , where is a constant, then the scaling laws can be written as [10]:
The parameters of the prototype plate are shown in Table 1.
Table 1The parameters of prototype plate
Rectangular plate | |||||
15 | 10 | 0.5 | 200 | 7.8 | 0.3 |
In order to determine geometric intervals of Eq. (12a) to Eq. (12c), it is assumed that the model and the prototype have the same materials, according to the analysis of the model shown in Table 2, to determine the approximate range of geometric intervals, namely the approximate range of .
Table 2Size parameters of the model
Model | |||||
M1 | 3 | 5 | 0.2 | 0.1 | 0.01 |
M2 | 0.6 | 25 | 0.2 | 0.5 | 0.01 |
M3 | 0.3 | 50 | 0.2 | 1 | 0.01 |
M4 | 0.2 | 75 | 0.2 | 1.5 | 0.01 |
M5 | 0.075 | 200 | 0.2 | 4 | 0.01 |
The first nature frequency of the prototype is 17.369 Hz. Based on Eq. (12a), Eq. (12b) and Eq. (12c), we can predict nature frequencies of the prototype and calculate the predicted discrepancy by using 5 kinds of models shown in Table 2, if the discrepancy , the predicted values are available [11], the predicted values are shown in Table 3.
Table 3The theoretical value, predicted value and errors under the three scaling laws (Eq. (12))
Nature frequency / Hz | Predicted by Eq. (12a) | Discrepancy | Predicted by Eq. (12b) | Error | Predicted by Eq. (12c) | Error | |
17.369 | – | – | – | – | – | – | |
M1 | 442.46 | 0.0885 | 994.9 % | 8.8492 | 49.05 % | 0.8849 | 94.91 % |
M2 | 667.72 | 3.3386 | 807.8 % | 13.3544 | 23.11 % | 6.6772 | 61.56 % |
M3 | 868.43 | 17.369 | 0.0 % | 17.369 | 0.0 % | 17.369 | 0.0 % |
M4 | 1202.6 | 54.117 | 211.57 % | 24.052 | 38.48 % | 36.078 | 107.71 % |
M5 | 4874.7 | 1559.9 | 8880.97 % | 97.494 | 461.31 % | 389.976 | 2145.24 % |
Analyzing the values shown in Table 3, the values predicted by Eq. (12b) is more accurate than the other method, so Eq. (12b) can be defined as the incomplete scaling law of the nature frequencies of elastic thin plates, and it is known that there are applicable geometric intervals within the range of M2–M4.
2.2. Analysis of the prediction discrepancy influence factors of elastic thin plates
Assuming the same materials and boundary conditions, incomplete similarity variables of elastic thin plates are the length , the width and the thickness . , where is the relationship of length of elastic thin plates’ sides, for rectangular thin plates.
The formula of nature frequency of four-side simply supported elastic thin plates can be written as [8]:
where, is the density of the plate, and are the numbers of half waves in the plate length and width direction respectively.
According to the relationship between the model and the prototype with the same vibration mode shape, we obtain:
The nature frequency of the model is represented as:
Multiply Eq. (15) by Eq. (12b), we can obtain:
The predicted discrepancy of incomplete geometric similarity can be defined as:
Substitute Eq. (14), Eq. (16) into Eq. (17), which can be simplified as:
According to Eq. (18), the following conclusions can be obtained:
(1) is independent, namely has no effect on the predicted discrepancy of incomplete geometric similarity;
(2) has no effect on the predicted discrepancy of incomplete geometric similarity, but does;
(3) The size parameters of prototype has no effect on incomplete geometric similarity applicable intervals, has effect on the intervals and mode shapes.
From above conclusions, we know that the geometric applicable intervals of simply supported elastic thin plates is the range of under different by using Eq. (12b) as the scaling law.
3. Example
3.1. Structure size intervals of the first-order nature characteristics
3.1.1. Applicable geometric intervals of distorted plate models
The geometrical parameters of the prototype plate: , , , , its material parameters are shown in Table 1. From the three above conclusions, we know that the analysis has general applicability by using the prototype.
Assuming , according to ANSYS calculation, the first-order nature frequency is .
The first-order nature frequency is respectively predicted as six discrete values then the relationship between the first-order natural frequencies and is obtained by fitting a fourth order polynomial:
Verify the curve by other discrete values in the range of , the step size of which is 0.05, and they fit the curve well, as shown in Fig. 2.
Fig. 2Verification of fourth-order polynomial fitting results
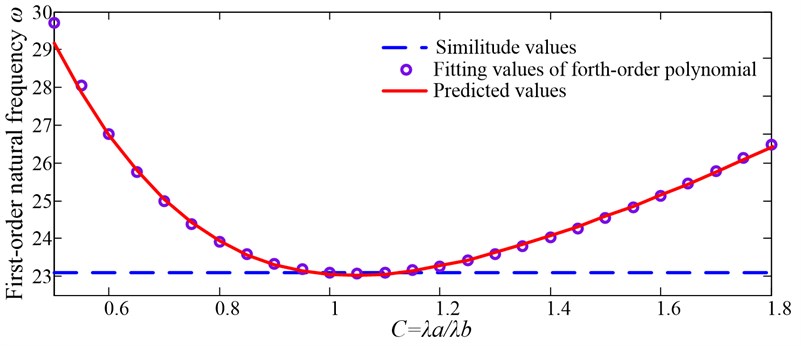
From Fig. 2, we know that Eq. (19) has accurate fitting effects in the range of .By introducing a ±10 % discrepancy of , the acceptable range of are calculated as:
The roots of Eq. () under the intervals are and . So, when , the applicable geometric interval is .
3.1.2. Boundary function
Calculating values of and under the corresponding by using the above method, as shown in Table 4, the fitting polynomial curves are shown from Fig. 3 to Fig. 6. The maximum value of 1.225 is based on the control intervals of shape modes in higher-order frequencies’ prediction below.
Fig. 3Fitting curve of Γ=1.0
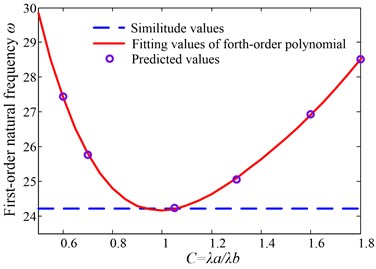
Fig. 4Fitting curve of Γ=1.1
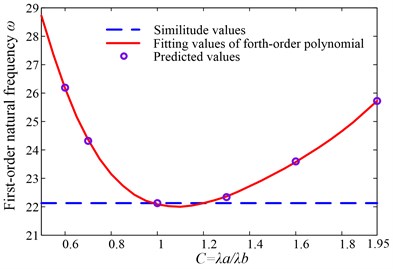
Fig. 5Fitting curve of Γ=1.15
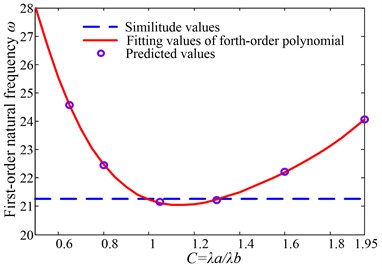
Fig. 6Fitting curve of Γ=1.225
Table 4Interval boundary values with different Γ
1.0 | 1.1 | 1.15 | 1.225 | |
Fourth order polynomial equations | ||||
Frequencies of the prototype / Hz | ||||
Boundary values |
From the boundary values of and the values shown in Table 4, we know:
By using fitting third-order polynomial, and can be written as:
The functional curves of Eq. (22) and Eq. (23) are shown in Fig. 7.
Fig. 7Boundary values of structure size applicable intervals
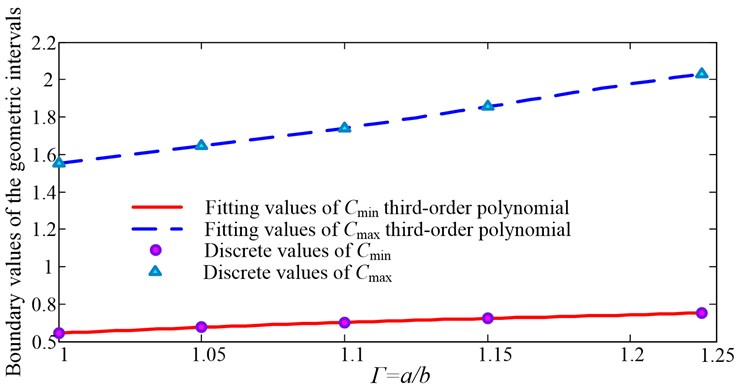
In Fig. 7, the area among the two cures is the applicable geometric intervals of first-order nature frequency of simply supported plates in the range of .
3.2. Structure size intervals of the higher-order nature characteristics
The geometric size distortion will cause the jump of thin plate models’ mode shapes, for the prototype in this paper, it is assumed that the range of size which can keep the same mode shapes between the model and the prototype is , as shown in Table 5.
Table 5Size intervals of each order
Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
– |
According to , the ratio of the length to the width of the plate model is:
For satisfying the prediction accuracy of higher-order nature frequencies of the plate model, and keeping the same mode shapes between the model and the prototype, so the model size is satisfied as:
where, represents the order number of nature frequency.
According to Eq. (24) and Eq. (25), the applicable geometric intervals of higher-order nature frequencies of the distorted model is:
where, is the predicted intervals of higher-order nature frequencies, is the mode shape control intervals of the prototype in this paper, their intersection is the applicable geometric intervals of higher-order nature frequencies in .
According to actual requirements, the range of is chosen based on different principles, so the range of each size is different, in this paper, choosing the mode shape control intervals based on the same first 8 modes, so .
It is different from the first-order nature frequency that the mode shapes of higher-order nature frequencies will change along with the change of , and it is difficult that and are obtained by using low-order polynomial fitting, considering the boundary values of applicable geometric intervals are the intersection of the predicted intervals of higher-order nature frequencies and the mode shape control intervals, so when analyzing the geometric intervals of higher-order nature frequencies by numerical method, the value of the plate model satisfies , solving the applicable geometric intervals of the fifth-order nature frequency of the prototype, as shown in 4.1.1.
Choosing , calculating the boundary values of the applicable geometric intervals by interpolation method, as shown in Table 6.
Table 6Interval boundary values of discrete Γ
Mode shape control interval | Discrete values | Fourth-order polynomial equations | The solution in control intervals | Boundary values of | |
According to the data shown in Table 6, we obtain:
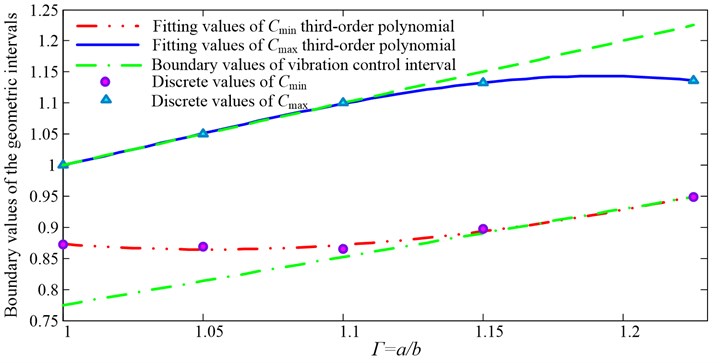
By using fitting third-order polynomial, and can be written as:
The functional images of Eq. (22) and Eq. (23) are shown in Fig. 8.
Fig. 8The fifth-order boundary values of structure size applicable intervals
4. Determination method and verification of the applicable geometric intervals
Choosing the simply supported plate under a certain mode shape as the example above, we obtain the geometric intervals boundary values , under different orders, as shown in Eq. (22), Eq. (23), Eq. (28) and Eq. (29) ,then the flow of the geometric intervals determination method is summarized and verified by a test.
Fig. 9Flow chart about determination of structure size applicable intervals
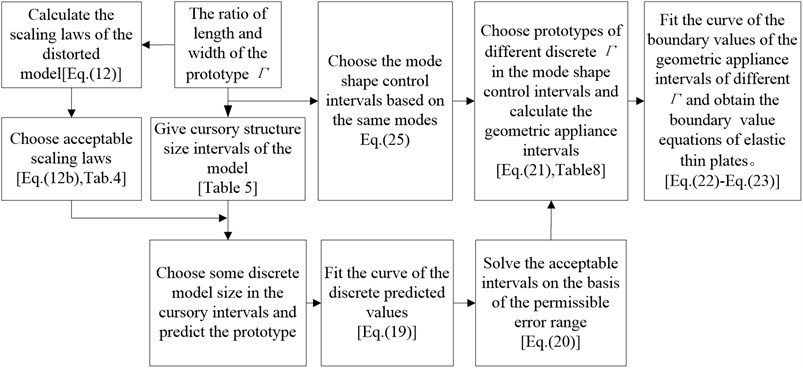
4.1. The flow of determination method
The flow chart about determination of geometric applicable intervals of elastic thin plates’ similar models is shown in Fig. 9.
4.2. Experiment
For the accuracy of the scaling laws and the intervals determination method, choose the titanium alloy single layer plates with same materials and different sizes as the experimental models, their parameters of materials and structural sizes are shown in Table 7.
Table 7Size of experimental plates
Length / mm | Width / mm | Thickness / mm | Young's modulus / GPa | Poisson's ratio | Density / kg/ | |
The prototype | 125 | 110 | 1.5 | 110.32 | 0.3 | 4420 |
The model | 90 | 80 | 1.5 | 110.32 | 0.3 | 4420 |
The ratio of length to width of the prototype is , that of the model is , , in the applicable geometric intervals, the values of nature frequencies of the prototype and the model, and the predicted discrepancy are shown in Table 8.
Table 8Comparison of prototype and scaling model’s experimental results
Order | Value of the prototype test / Hz | Value of the model test / Hz | Predicted value of the prototype / Hz | Error between the prediction and the test / % |
1 | 71.362 | 127.71 | 67.685 | 5.1526 |
2 | 193.78 | 385.08 | 204.08 | 5.3167 |
3 | 432.56 | 788.74 | 418.02 | 3.3618 |
4 | 663.39 | 1317.0 | 698.01 | 5.2215 |
5 | 754.08 | 1547.1 | 819.95 | 8.7364 |
6 | 1210.5 | 2232.4 | 1183.14 | 2.2574 |
From Table 8, we know that the predicted values of the model are accurate in applicable geometric intervals, and it is verified that the applicable geometric intervals are valid for the design of similar models.
5. Conclusions
In this paper, the determination method of applicable geometric intervals boundary value of thin rectangular plates was studied, and the boundary value equations of the applicable intervals of nature frequencies was obtained and analyzed. Furthermore, the experiments of the titanium alloy single-layer plates with same materials and different sizes are studied; the conclusions are listed as follows:
(1) The incomplete scaling laws of the distorted model of elastic thin plates are set up, and the predicted discrepancy influencing factors from the model to its prototype were obtained.
(2)The mode shapes control interval ( in this paper) is studied based on the same first 8 modes, the boundary value equations of applicable geometric intervals of nature frequencies are obtained by using twice interpolation method in the mode shape control intervals.
(3)It is verified by the experiment that the models which are selected based on the interval boundary value equations can predict nature characteristics of the prototype accurately.
References
-
Soedel W. Vibrations of shells and plates. CRC Press, 2004.
-
Rezaeepazhand J, Yazdi A. A. Similitude requirements and scaling laws for flutter prediction of angle-ply composite plates. Composite part B – engineering, Vol. 42, Issue 1, 2011, p. 51-56.
-
Bachynski E. E., Motley M. R., Young Y. L. Dynamic hydroelastic scaling of the underwater shock response of composite marine structures. Journal of applied mechanics transactions of the ASME, Vol. 79, Issue 1, 2012, p. 501-507.
-
Li Shirong, Zhang Jinghua, Xu Hua Linear transformation between the bending solutions of functionally graded and homogenous circular plates. Journal of theoretical and applied mechanics, Vol. 32, Issue 5, 2011, p. 121-125, (in Chinese).
-
Zhang Zhenhua, Qin Jian, Wang Cheng, Li Zhenhuan, Zhu Xi Method for scaling impact load data obtained from a small scale model to that of the full size clamped and stiffened plate. Journal of Harbin Engineering University, Vol. 29, Issue 3, 2008, p. 226-231, (in Chinese).
-
Singhatanadgid P., Ungbhakorn V. Scaling laws for vibration response of anti-symmetrically laminated plates. Structural engineering and mechanic, Vol. 14, Issue 3, 2002, p. 345-364.
-
Simitses G. J. Structural similitude for flat laminated surfaces. Composite structures, Vol. 51, Issue 2, 2001, p. 191-194.
-
Rezaeepazhand J., Simitses G. J., Starnes J. H. Use of Scaled-down Models for predicting vibration response of laminated plates. Composite structures, Vol. 30, Issue 4, 1995, p. 419-426.
-
Cao Zhiyuan Vibration theory of plate and shell. Beijing: China railway publishing company, 1983, (in Chinese).
-
Simitses G. J., Rezaeepazhand. J. Structural similitude and scaling laws for laminated beam-plates. American society of mechanical engineers, aerospace division (publication) AD, Vol. 26, 1992, p. 37-45.
-
Simitses G. J., Rezaeepazhand J. Structural similitude and scaling laws for buckling of cross-ply laminated plates. Journal of thermoplastic composite materials, Vol. 8, Issue 3, 1995, p. 240-251.
About this article
This work is supported by National Science Foundation of China (51105064), National Program on Key Basic Research Project (2012CB026000), and Natural Science Foundation of Liaoning Province (201202056).
