Abstract
Conventionally a railway vehicle has stable motion in low speeds, when it reaches to high speeds stability changes to unstable form. The main purpose of this article is to show the authors' view of analytical investigation of bifurcation, nonlinear lateral stability and hunting behavior of rail vehicles in a tangent track. The paper includes nonlinear primary yaw dampers, and flange contact and also bogie existence. This study contains Bogoliubov method for the analysis. Linear and nonlinear critical speeds are obtained, and changing parameters' effect in differing the speeds with altered lateral stiffness in primary suspension system has been studied. General works about hunting phenomenon show that nonlinear critical speed is less than linear one.
1. Introduction
A limiting factor in high speed rail vehicles is the dynamic phenomenon called “hunting”, which initially becomes apparent as a lightly damped lateral/yaw response of the vehicle. Above a certain forward speed, called the “critical speed”, hunting appears as an undamped motion of the wheelset constrained by the wheel flange and the rail. The wheelset hunting can cause truck (bogie) hunting and eventually lead to body or primary hunting. Primary hunting can cause large lateral forces at the rail that can lead to derailment. Two hunting categories are introduced, primary which appears in low speeds and can be controlled by sufficient dampers, secondary hunting which is seen in high speeds and is a self-excited happening and cannot be disappeared or run away from [1].
Secondary hunting can be omitted by designing the vehicle to have critical speed in higher speeds at which the vehicle is working around. Primary hunting can cause large lateral forces at the rail that can lead to derailment. When the vehicle speed increases beyond a certain limit, the steady motion loses its stability and hunting starts. Further, the system phase diagram bursts out from the fixed point when the vehicle speed is above the critical speed, closely resembling the Hopf bifurcation phenomenon.Dynamic stability for a multiple degree of freedom railway vehicle without containing flange contact was studied by Yang-Tsai Fan and Wen-Fang Wu [2]. Differences between considering some DOFs in the system for hunting stability were verified [3]. Changing some parameters which led to different forms of hopf bifurcations was done by O. Polach [4]. Due to its importance to the operation of rail vehicles, hunting has been studied for several decades [5]. The early works generally used linear models that gave a limited view of the problem. Subsequent studies by Law and Brand [6], Abel and Cooperrider [7] Hedrick and Arslan [8], extended the linear model to magnify the effects of nonlinearities in the system. Analysis of nonlinear systems needs bifurcation study and its influences.
Bifurcation is a dynamical behavior of nonlinear systems when the system parameters change. Hopf bifurcation is a kind of bifurcation in which the stability of limit cycle changes. Huilgol [9] first investigated the Hopf bifurcation in a wheelset, taking into account the nonlinear contact force between the wheel and rail. Subsequently, a group of scientists led by True [10, 11] further studied the bifurcation in two rail truck models introduced by Cooperrider [12]. They considered nonlinearities due to the creep-creep force relationship and the effect of the nonlinear contact geometry between realistic wheel and rail profiles. They found that subcritical Hopf bifurcation is common in rail vehicles [13, 14].Yang and Ahmadian [15] studied the influence of yaw damping nonlinearities on Hopf bifurcation in a flangeless wheelset. Their investigation showed that hunting amplitude increases rapidly when forward speed is beyond the linear critical speed. This indicates that the wheel lateral displacement exceeds the gauge clearance (the clearance between the wheel flange and railhead) and flanging occurs. Flanging is referred to as the contact between wheel flange and railhead. Eliminating the flange dynamics from the model can introduce gross errors.Yang and Ahmadian also studied Hopf bifurcation and hunting behavior in a single rail wheelset with flange contact [16]
We will add a bogie to wheeset for studying the effect of bogie presence in hunting behavior of single wheelset, and check all the parameters’ influence on critical speeds (linear and nonlinear critical speeds).The lateral movement which adds one DOF to wheelset that has two DOF makes our system a three degree of freedom system. In this paper it is assumed that creep forces remain small and do not grow to complicated form, but suspension's forces become nonlinear and flange contact occurs in some cases. The actual damping force is of the primary yaw damper is known as a polynomial. The effects of different parameters on linear and nonlinear critical speeds are examined.
Fig. 1Bogie and wheelsets configuration
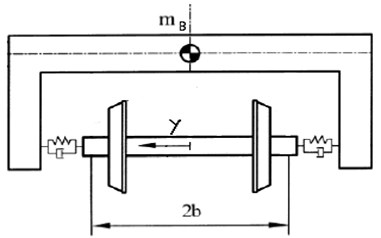
a)
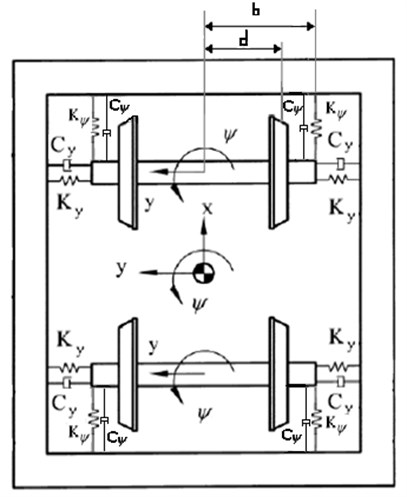
b)
2. Equation of motion and force modeling
A wheelset with lateral and yaw movement and a bogie with only lateral movement are considered, and the flange contact is presented. The wheel profile is conical with conicity . Wheelset lateral differential equation of motion is [17]:
Forces in equations are known as:
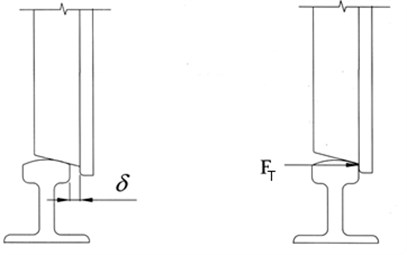
The flange contact force, , is modeled as a nonlinear spring with deadband equal to the flange clearance. It is mathematically described as:
where and are rail lateral stiffness and flange clearance. Flange clearance represents deadband between wheel flange and railhead (shown in Figure 3). It says that when the lateral displacement of the wheelset is more than, rail plays the role of a spring that pushes the wheel against its movement to the rail by the force which is defined by equation (3).
Fig. 2Wheel flange/rail clearance and flange contact force
Yaw differential equation of motion for single wheelset is described as:
where:
indicating lateral suspension force and yaw moment. is defined by:
is relative velocity of the longitudinal yaw damper.
For bogie, because only lateral motion is presented, the equation added to system with this form:
3. Analytical solution
If we take the equations of motion to state space, then the state vector would be:
This shows the lateral and yaw motions of wheelset and also the lateral motion of the bogie.
Writing equations (1, 4, and 7) in matrix form, we have:
We divided the system into linear and nonlinear parts. shows the nonlinear terms and the elements of the matrix are described as:
is the control parameter in this study. is the speed in which the hunting motion initiates in linear analysis (when the eigenvalues become positive). By using Taylor series around we will have:
In these equations, denotes difference between the bogie's forward speed and (perturbation of the speed) and is a small factor. After mixing equations (8) and (9) then:
where:
By using Bogoliubov method, the answers are approximated by:
where is determined by initial condition, are real parts and are imaginary parts of eigenvectors for which has the purely imaginary eigenvalues ( is fundamental natural frequency for linearized system). , are obtained by first-order approximation [18]:
where and are symbolically calculated by:
are real parts and are imaginary parts of eigenvectors corresponding to . When , the steady solution is gained and in this situation, the stationary limit cycle’s amplitude can be got. Of course the nontrivial solution for this part is acceptable. For examining the stability of the limit cycle we have:
Table 1Parameter values
Parameters | Values |
Mass of the wheelset | 264.448 kg |
Roll moment of inertia | 625.7 kg m2 |
Spin moment of inertia | 133.92 kg m2 |
Wheel radius | 0.533 m |
Half of the track gauge | 0.71755 m |
Wheel conicity | 0.05 rad |
Axle load | 1.8×104 N |
Half of the yaw suspension arm | 1 m |
Lateral stiffness | 8.67×104 N/m |
Lateral damping | 2.1×104 N/m |
Yaw spring stiffness | 8.67×105 N/m |
Lateral creep force coefficient | 1.5913×106 N |
Spin creep force coefficient | 2000 Nm2 |
Lateral spin creep force coefficient | 1.2×105 Nm |
Longitudinal creep force coefficient | 1.9135×107 N |
Stiffness of flange contact force | 1.617×107 N/m |
Gauge clearance | 0.923 cm |
Damping coefficients for primary yaw damper | 1.923×104, 5.14×105, –3.1127×104, 5.14×106 |
Fig. 3Difference between hopf bifurcation diagrams for wheelset and bogie with wheelset
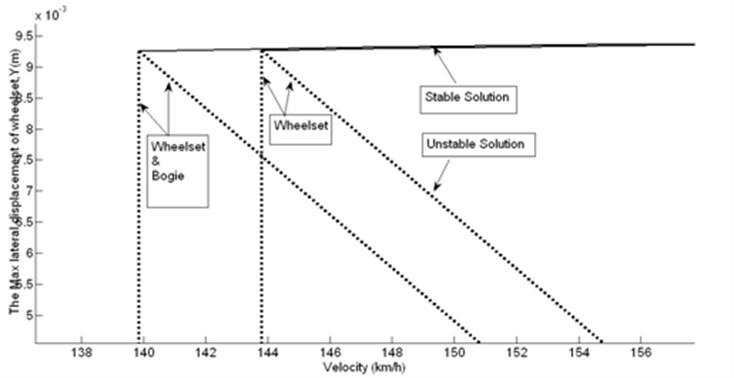
Figure (3) shows the bifurcation diagram for two systems. 1 – Wheelset. 2 – Bogie and wheelsets. The critical speeds in wheelset system are 155 km/h for linear speed and 144 km/h for nonlinear one, but for the second system which contains bogie's lateral movement the speeds are lower. It represents for suggesting limit speeds for bogie, just analyzing wheelset is not safe. For bogie the saddle-node bifurcation starts at 140 km/h and the Hopf bifurcation point is at 151 km/h. The speed between these two speeds is a risky one because according to system parameters and conditions the motion can be stable or unstable. Before 140 km/h for all excitations of system the long time answer would be stationary without oscillation so hunting will not occur in this range. After linear critical speed the motion suddenly changes its character and reaches to a highly amplitude oscillation and derailment happens. The safest speed for not seeing any hunting is below 140 km/h.
4. Parametric study
A parametric study for determining primary lateral stiffness and changing every other parameter is done in this paper.
4.1. Wheelset mass
Fig. 4Effect of different wheelset mass with different lateral stiffness on critical speeds
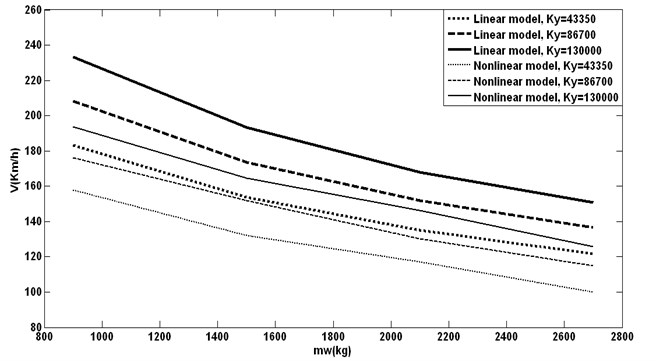
By increasing lateral stiffness in primary suspension system, both linear and nonlinear critical speeds increase. In this case if we use higher mass for wheelset, both speeds will have sensible decrease. This leads to worse hunting behavior.
4.2. Wheelset radius
Fig. 5Effect of different wheel radius with different lateral stiffness on critical speeds
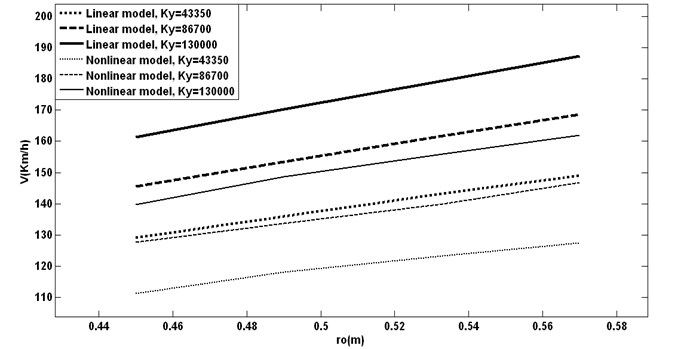
Increasing in wheels radius causes better results for hunting, but of course we cannot have a very big wheel. It is limited by the UIC standard. This shows that after using a system, we need to cut the wheel off because of irregularities on its surface, and we must be careful that decreasing the radius by cutting off takes the critical speeds to lower ones.
4.3. Half of the gauge track
Fig. 6Influence of changing half of the gauge track with different lateral stiffness on hunting behavior
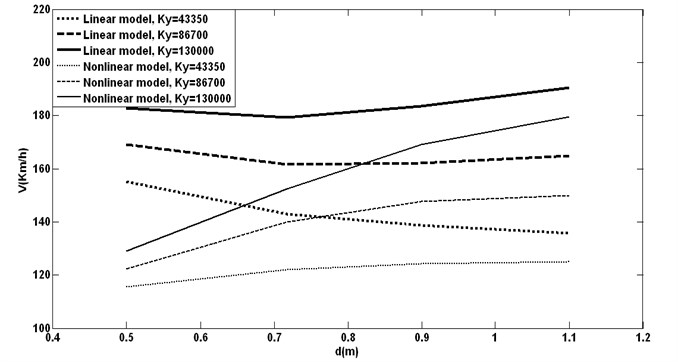
Using a wheelset with longer axle or a wider track leads to lower linear critical speeds which is not good for hunting design. On the other hand nonlinear critical speeds get higher which is good in hunting. Evantually because first we meet nonlinear speed and then linear one,and the nonlinear one grows and also the range between linear and nonlinear speeds becomes smaller (range of having hunting motion gets smaller), this change is suitable for hunting behavior.
4.4. Equivalent conicity
Fig. 7Equivalent conicity changing with different lateral stiffness vs. critical speeds
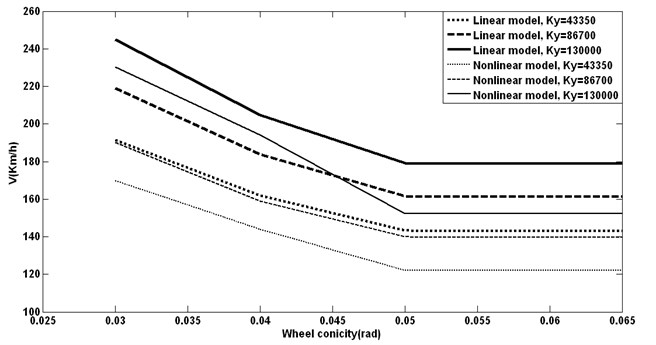
4.5. Axle load
Higher equivalent conicity causes lower critical speeds (near and nonlinear). This is not acceptable in hunting. Although increasing too much for conicity will not be effective, we have to choose a suitable wheel profile that has low equivalent conicity.
Fig. 8Axle load effects with different lateral springs on hunting speeds
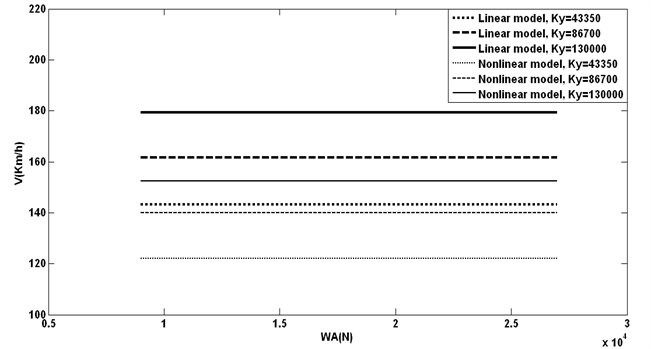
As shown in this figure changing does not have effective influence on critical speeds. The most important reason for this happening is differential equation of motion. In equations (1, 4) the coefficient for is very small, and by increasing in very high amount, the changes in hunting speeds would be seen.
4.6. Primary lateral damping
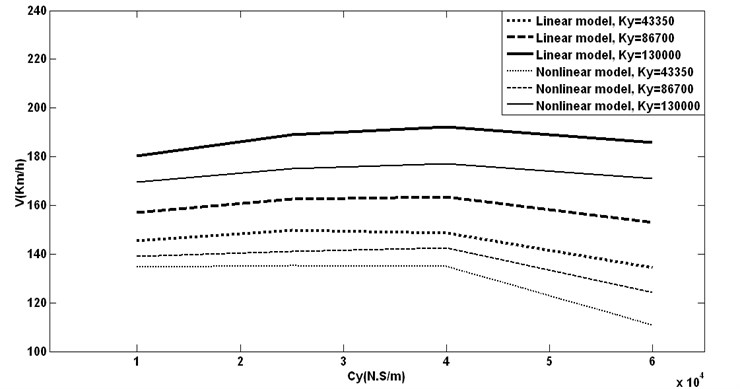
Nonlinear critical speed is first seen and then linear critical speed. Unpredictable linear hunting speed changing will not make serious problem in suggesting good primary lateral damping. Nonlinear hunting speed changing shows that high brings about low velocities for hunting that leads to bad hunting treatment. In low we see no changing in critical speeds.
Fig. 9Different primary lateral damping and stiffness vs. critical speeds
4.7. Yaw spring stiffness of primary suspension
Fig. 10Yaw and different lateral stiffness vs. hunting speeds
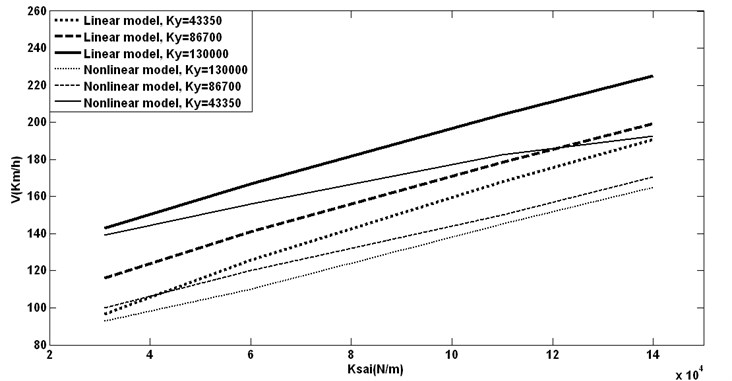
As it is clear in this figure both speeds grow while high yaw stiffness presents. In equation of motions for wheelset yaw and lateral movements are coupled. For all the figures we see that high is equal to higher critical speeds, so higher would be like higher . By this better hunting behavior is seen.
4.8. Half of the primary yaw spring arm
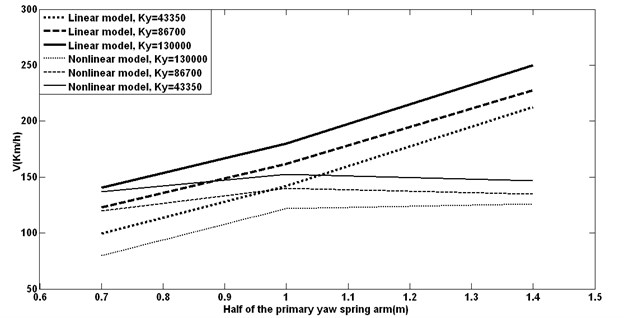
Absolute increasing in linear critical speeds is seen by having growth in half of the primary yaw spring arm, but first growing and after 1 m decreasing smoothly for nonlinear critical speed is presented. Best point for hunting is 1 m because the most nonlinear hunting speed is there and also the shortest range between linear and nonlinear critical speeds exists.
Fig. 11Half of the primary yaw spring arm with different lateral stiffness vs. critical speeds
4.9. Rail stiffness
Fig. 12Rail stiffness with different Ky vs. hunting speeds
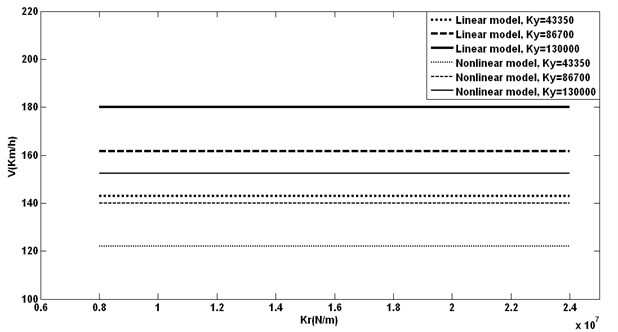
Changing rail stiffness causes no effect on hunting speeds. The only effect it may cause is on lateral forces while flange contact occures that lead to derailment.
4.10. Flange clearance
Fig. 13Flange clearance and different Ky vs. critical speeds
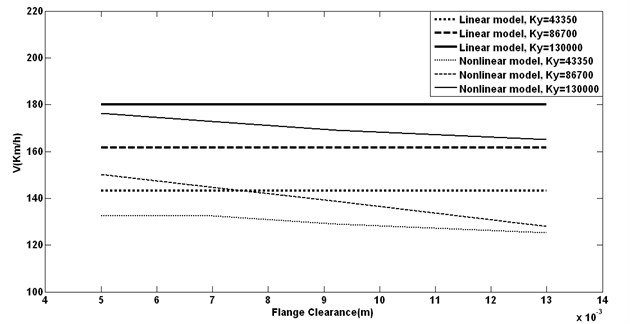
Bigger flange clearance makes no change for linear critical speeds, but nonlinear ones become less. Increasing the clearance causes two problems, first is having low nonlinear hunting speed and second one is letting the flange have more inertia while compacting the rail that is very dangerous for derailment.
4.11. Bogie mass
Fig. 14Bogie mass with different pramary lateral stiffness vs. hunting speeds
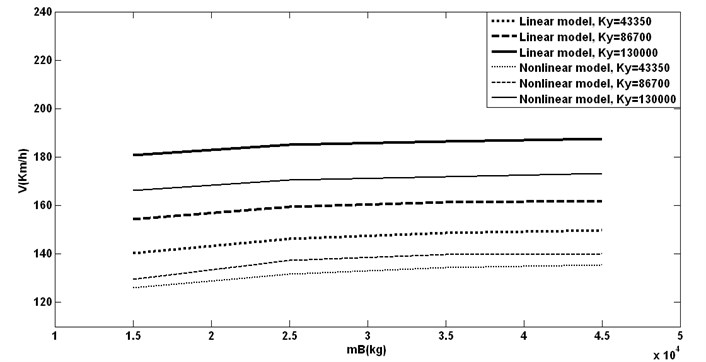
No serious changing for bogie mass between 15000 kg and 45000 kg is presented. A small increasing in both hunting speeds is seen which is good for hunting behavior.
5. Conclusions
Linear and nonlinear hunting speeds were investigated, and the influence of changing parameters in differing the speeds with various lateral stiffnesses in primary suspension system has been studied. The results of the study show that the system with bogie and wheelset has less critical speeds than wheelset system alone. It shows that for obtaining critical speeds studying complete system in more accurate and safe. The wider the track according to standard the better the hunting behavior. Conicity is another parameter which affects highly in hunting speeds and high conicity causes low critical speeds. Axle load and rail stiffness do not have influence in hunting speeds. Changing in flange clearance does not alter the linear speeds but makes the nonlinear ones less which is a disadvantage for hunting behavior.
References
-
Krzysztof Z., Miroslaw D. Self-exciting vibration and Hopf bifurcation in nonlinear stability analysis of rail vehicles in a curved track. European Journal of Mechanics A/Solids, Vol. 14, 2009, p. 1-14.
-
Fan Y. T., Wu W. F. Stability analysis of railway vehicle and it's verification through field test data. Journal of the Chinese Institute of Engineers, Vol. 13, 2006, p. 493-505.
-
Lee S. Y., Cheng Y. C. Hunting stability analysis of high-speed railway vehicle trucks on tangent tracks. Journal of Sound and Vibration, Vol. 18, 2005, p. 881-898.
-
Polach O. On nonlinear methods of bogie stability assessment using computer simulations. IMechE, Part F: J. Rail and Rapid Transit, Vol. 220, 2005.
-
Law E. H., Cooperrider N. K. A survey of railway vehicle dynamics research. ASME Journal of Dynamic Systems, Measurement and Control, Vol. 96, Issue 5, 1974, p. 132-146.
-
Law E. H., Brand R. S. Analysis of the nonlinear dynamics of a rail vehicle wheel set. Journal of dynamic systems, Measurement and Control, Series G, Vol. 95, 1973, p. 28-35.
-
Abel S. G., Cooperrider N. K. An equivalent linearization algorithm for nonlinear system limit cycle analysis. ASME Journal of Dynamic Systems, Measurement and Control, Vol. 107, 1985, p. 117-122.
-
Hedrick J. K., Arslan A. V. Nonlinear analysis of rail vehicle forced lateral response and stability. ASME Journal of Dynamic Systems, Measurement and Control, Vol. 101, 1979, p. 230-237.
-
Huilgol R. R. Hopf-Friedrichs Bifurcation and the hunting of a railway axle. Quart. J. Appl. Math., p. 85-94.
-
True H. A method to investigate the nonlinear oscillations of a railway vehicle. Applied Mechanics Rail Transportation Symposium – presented at the winter annual meeting of ASME, 1988.
-
True H., Kaas-Petersen C. A bifurcation analysis of nonlinear oscillations in railway vehicles. In The Dynamics of vehicles on road and on tracks, 8th IAVSD Symposium, 1984, p. 438-444.
-
Cooperrider N. K. The hunting behavior of conventional railway trucks. ASME Journal of Eng. Industry, 1972, p. 752-762.
-
True H. Some recent developments in nonlinear railway vehicle dynamics. In 1st European Nonlinear Oscillation Conference, Proceedings of the International Conference, Hamburg, 1993, p. 129-148.
-
True H. Does a critical speed for railroad vehicle exist? In Proceedings of the IEEE/ASME Journal Railroad Conference, 1994, p. 125-131.
-
Yang S., Ahmadian M. The Hopf bifurcation of a railway wheelset with nonlinear damping. In proceedings of rail transportation Division, ASME International Mechanical Engineering Congress and Exposition, Atlanta GA, 1996, p. 113-120.
-
Yang S., Ahmadian M. Hopf Bifurcation and Hunting Behavior in a Rail Wheel set with Flange Contact. Journal of Nonlinear Dynamics, 1998, p. 15-30.
-
Garg V. K., Dukkipati R. V. Dynamics of Railway Vehicle Systems. Academic Press, Canada, 1984.
-
Bogoliubov N. N., Mitropolsky Y. A. Asymptotic method in the theory of nonlinear oscillations. Hindustan Publishing, Delhi, India, 1961.
