Abstract
To overcome the shortages of current laminated rubber bearings (RB), a new kind of isolator called Prestressed Rubber Bearing (PRB) is presented in this paper, which is invented by appropriately amplifying the thickness of rubber layers in conventional RB and employing prestress tendons. Based on the experimental study, a modified formula for vertical stiffness of PRB is established. Then the nonlinear analytical model for PRB’s horizontal stiffness is developed and the corresponding formulas are derived. Through the response history analysis of structures, the isolation capacities of PRBs are investigated. The results show that the horizontal stiffness of PRB is variable with the displacment. PRB not only has effective isolation capacity as conventional RBs but also has the favorable capacity of horizontal displacement limitation and vertical up resistance.
1. Introduction
Isolators are the key components of the isolated structures. At present, the most widely used isolators are laminated Rubber Bearings (RB), in which the steel plates and rubber layers are arranged alternately and combined by high-temperature and vulcanization [1]. There are some disadvantages existing in current RBs: (i) the capacity of horizontal displacement limitation is inadequate. The earthquake may cause large horizontal displacement in the isolators and reduction of effective bearing area, which may result in overturning of RBs due to the large second order moment [2]; (ii) the tensile strength is inadequate. The internal tensile force is forbidden in conventional RBs according to current Chinese Code. However, it is difficult to avoid in some situations, especially for the high rise buildings; (iii) the vertical isolation is inadequate. Many earthquake disasters have shown that lots of non-structural damages were caused by vertical vibration. Although thick rubber layers may produce good capacity of vertical isolation, they also may lead to the uneven settlement of superstructure when it is constructed. So the thin rubber layers are used in current RBs.
To overcome the disadvantage of conventional RBs, several related studies were conducted. Kang et al. proposed fiber reinforced elastomeric isolator which used the carbon fiber or the glass fiber instead of steel plate to improve the vertical isolation capacity of RB [3]. Ismail [4] introduced a new seismic system, named roll-n-cage isolator (RNC). The main bearing mechanism of the RNC is a hollow elastomeric cylinder of a designed thickness around a rolling body. The device incorporates isolation, energy dissipation, and inherent gravity-based restoring force mechanism in a single unit. Amarnath Kasalanati proposed an uplift prevention mechanism which employs prestress theory to develop sufficient compressive force on the isolator [5]. Peng Tian Bo [6] developed a double spherical aseismic bearing, which increased the natural vibration period of buildings by increasing the centre distance of spheres. Zhou Xiyuan [7] and Cui Yibin [8] presented a kind of rubber isolator with a steel bar inside to limit the deformation of isolator. Zhang Yongshan [9] and Wei Liushun [10] proposed a 3-dimensional isolation device, in which the vertical isolation capacity was developed by employing a semi-active controlled hydro-cylinder parallelly connected with vertical spring.
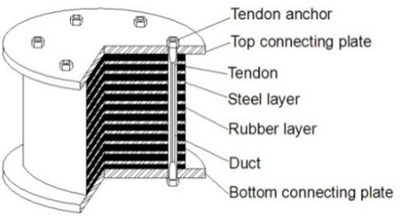
However, these devices can not overcome all of the conventional RBs’ shortcomings. This paper proposes an innovative type of rubber bearing, named as Prestressed Rubber Bearing (PRB) [Chinese Patent Number: ZL201020181364.1]. As shown in Fig. 1, PRB is developed based on conventional RB. The thicknesses of rubber layers are increased appropriately to improve the capacity of vertical isolation. Several vertical ducts are set and prestress tendons are installed. Although the thicknesses of rubber layers in PRBs are larger than the conventional RBs, the prestress force can achieve most of the vertical deformation before the superstructure is constructed. So the problem of uneven settlement can be eliminated. On the other hand, because of prestress tendons, PRB has the capacity of horizontal displacement limitation and up-lift resistance.
Fig. 1Structure of PRB
This paper develops the nonlinear analytical model for the deformation of PRB. The formulas for both vertical stiffness and horizontal stiffness of PRB are proposed. Through numerical analysis, the isolation capacity of PRB is also investigated.
2. Vertical stiffness
The vertical stiffness is one of the important mechanical properties for PRB. Currently, the vertical stiffness of RB is calculated using formula proposed by Lindley as [11]:
where is the diameter of cross section; is the second shape factor of RB, ; is the number of rubber layers; is the modified elasticity modulus of the bearing , ; is the elasticity modulus of volume constrained rubber; is the elasticity modulus of rubber; is the correcting coefficient for the rubber hardness; is the first shape factor of RB which is the ratio of bearing area to the free surface area, ; is the diameter of the ducts; is the number of ducts.
The vertical monotonic loading tests are conducted to study the vertical stiffness of the PRB. A computer controlled compression testing machine with maximum load capacity of 300 kN and maximum stroke of 500 mm (Fig. 2) is used. The 6 groups of specimens (each group has 3 same specimens) are tested. The height of bearing before applying prestress force is 172 mm, the diameter of effective cross sectional area is 150 mm, and the diameter of ducts is 15 mm. The hardness of rubber is 60 HA and the yield strength of steel plate is 235 MPa. The detailed parameters of specimen are listed in Table 1, where is the thickness of rubber layer; is the thickness of rubber plate.
Experimental results show that Lindley formula greatly underestimates the vertical stiffness of RBs with thicker rubber layer. The vertical stiffness calculated from Lindley’s formula is about 50 % of the experimental values. It is mainly due to the reason that Lindley formula underestimates the steel plates’ constraint to rubber layers when rubber layers become thicker. Therefore, the Lindley’s formula needs to be modified for the RB with thick rubber layers as follows:
where is the vertical stiffness of PRB; is effective area of cross-section; is a modifying coefficient of vertical stiffness. By linear regression analysis of test results, the modifying coefficient can be obtained as:
Fig. 2Experimental set-up of vertical loading test
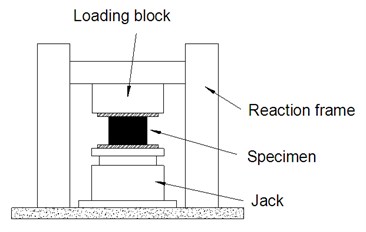
(a) Sketch of experimental setup

(b) Experimental site
Table 1Parameters of specimens
Specimen group | / mm | / mm | ||
PRB-1 | 10.6 | 1 | 2.08 | 0.94 |
PRB-2 | 9.24 | 1 | 2.38 | 0.95 |
PRB-3 | 7.7 | 1 | 2.86 | 0.97 |
PRB-4 | 9.6 | 2 | 2.29 | 1.04 |
PRB-5 | 8.2 | 2 | 2.67 | 1.07 |
PRB-6 | 6.7 | 2 | 3.29 | 1.12 |
The vertical stiffness of the bearings mainly depends on the deformation of rubber layers. The first shape factor is an important parameter indicating the steel plates’ constraint on the deformation of the rubber layers. The relationship of vertical stiffness and is shown in Fig. 3, in which the results from Lindley’s formulas, Eq. (2) and the experiments are compared. It can be seen that vertical stiffness of PRB increases with increase of . The main reason is that the thickness of rubber layers decreases when the value of increases. Hence, the steel plates’ constraint on the deformation of the rubber layers increases. And the vertical stiffness increases.
Fig. 3Relationship between vertical stiffness and S1
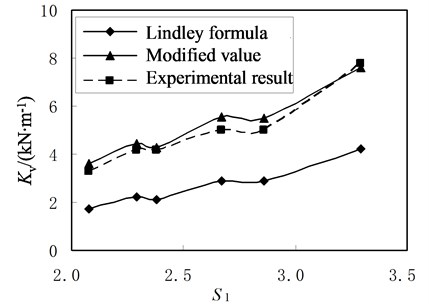
The accuracy of the proposed formula depends on the number of regression samples. Because only 18 samples are used in regression analysis, the proposed modifying coefficient can only be applied to the PRB with similar dimension.
3. Horizontal stiffness
Horizontal stiffness is one of the most important mechanical properties for the isolation bearings. The horizontal stiffness for the conventional RB is calculated as [12]:
where is the shear modulus of the rubber.
The horizontal deformation mechanism of PRB is different from the conventional RBs. Due to the deformation compatibility of tendons and rubber layers, the prestress tendon will be subjected to tension and the rubber layers will be subjected to compression when horizontal deformation happens. Therefore, the horizontal component of prestress tendons’ internal force could change the stiffness of PRB. Eq. (4) is not valid for calculating the horizontal stiffness of PRBs.
3.1. Model development
Fig. 4 is the analytical model for the horizontal stiffness of PRB. When the prestress force is applied, the PRB is shortened the amount of , and the height of PRB at this moment is defined as . When the gravity load of supper-structure is applied, the PRB is shortened the amount of . And finally, when the horizontal load is applied, the PRB is shortened the amount of . The height of PRB at this moment is defined as , .
Fig. 4Analytical model of PRB
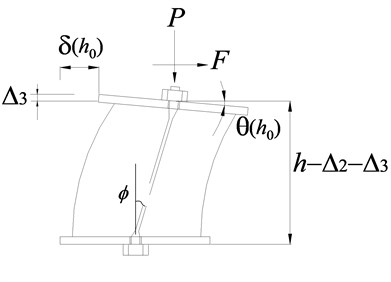
Fig. 5Slider of PRB
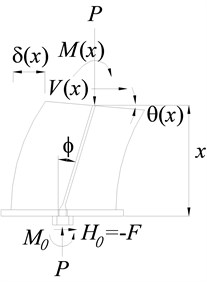
To simplify the analysis, the following assumptions are adopted: (i) all tendons are incorporated into an equivalent tendon which is located in the center of cross-section; (ii) the tendon remains straight when the bearing has horizontal deformation. The vertical equilibrium equation can be obtained as follows:
where , is the elasticity modulus of prestress tendon and the equivalent cross-sectional area of the tendon respectively; is the inclination of the tendon; is the horizontal displacement in the top of PRB, which can be calculated as:
Substituting Eq. (6) into Eq. (5):
Considering the lower part of PRB as shown in Fig. 5, the constitutive equation can be written as:
where is the horizontal displacement at the height of ; is the cross-section’s deflection angle at the height of ; is the equivalent shear stiffness of the PRB; is the equivalent bending stiffness of PRB. They can be computed by:
where is the moment inertia of cross-section; is determined by:
where .
Therefore the equations of equilibrium can be written as:
From Eqs. (8), (9), (12), (13), the value of and can be obtained as:
Substituting Eq. (14), Eq. (15) into Eq. (12) and Eq. (13), we can obtain:
The general solution of Eq. (16) is:
in which .
Substituting Eq. (17) into Eq. (12) and Eq. (13), it can be obtained that:
Considering the boundary conditions: , and , the coefficient can be obtained as:
Therefore, the horizontal displacement of the bearing along the height is:
And the bending angle of the cross-section is:
Hence, the horizontal displacement at the top of bearing is:
And the horizontal stiffness of PRB is:
From the Eq. (22), it can be seen that the value of is the function of variable , , and . Because and are coupled with each other, the value of can not be obtained directly. The iterative method can be used. Assuming the initial value of , the value of can be computed by Eq. (7). Then the value of can be calculated. After that the value of can be updated in Eq. (7). These steps are iterated until the value of satisfies the accuracy requirement.
If the rotation of the top connecting plate is constrained, , it can be obtained by Eq. (24):
After solving the Eq. (27) and Eq. (7), the horizontal stiffness of PRB can be computed directly.
3.2. Numerical investigation
A hypothesis cylinder PRB is used to conduct the numerical investigation. The diameter of cross-section is 150 mm and the height before applying prestress force is 168 mm. The thickness of a single rubber layer and a single steel layer are 8 mm and 2 mm respectively. There are 6 ducts of diameter 15 mm setting along the range of PRBs. The diameters of prestress tendons are 8 mm, and the total cross area is 300 mm2. The elasticity modulus of tendons is 2.0×105 N/mm2. The JIS hardness of the rubber is 60 HA.
3.2.1. Influence of prestress tendons
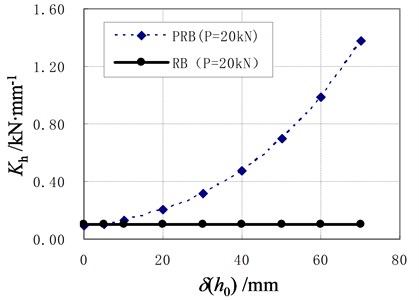
It is assumed that the vertical load is 20 kN and the prestress force is equal to the vertical load. Hence, the value of is zero. The horizontal stiffness of PRB and RB are computed by equations in Section 2.1 and shown in Fig. 6.
It can be seen that the horizontal stiffness of PRB is variable with the horizontal displacement, which is completely different from the stiffness of conventional RB. When the horizontal displacement is small, PRB’s stiffness is close to RB’s. The stiffness of PRB increases as the horizontal displacement increases. The main reason is that the horizontal component of tendons’ internal force is resisting part of horizontal loading. When the displacement increases, the horizontal component of internal force also increases. Hence the horizontal stiffness of PRB increases.
Fig. 6The horizontal stiffness of PRB and RB
3.2.2. Influence of vertical load
Fig. 7 shows the relationship between the initial horizontal stiffness and vertical load. It can be seen that the initial stiffness of PRB depends on both the height of bearing and the vertical load. The initial stiffness decreases with the increase of vertical load. This is due to the reason that the second order bending moment in PRB is increased when the vertical load increases. So the capacity of resisting horizontal forces is reduced. And the initial horizontal stiffness is reduced. The stiffness decreases to zero when the vertical load reaches a critical value. In this situation the buckling of PRB occurs. Therefore, the vertical loading capacity of PRB is determined by stability.
It can also be seen from Fig. 7 that the initial stiffness of PRB decreases with the increase of bearing height. The initial stiffness of PRB is close to the horizontal stiffness of RB with similar dimensions. Generally, the horizontal stiffness of RB decreased with the increase of overall rubber layers height. Therefore, the initial stiffness of PRB decreases as the bearing height increases.
3.2.3. Influence of rubber layer’s thickness
When the vertical load is 20 kN and the horizontal displacement at the top of PRB is 40 mm, the relationship between the horizontal stiffness and the ratio of to is obtained and shown in Fig. 8.
Fig. 7Relationship between initial horizontal stiffness and vertical load
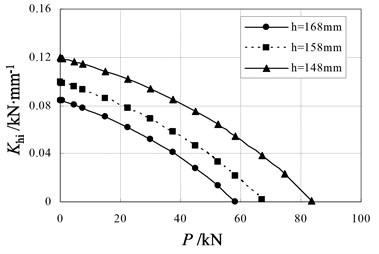
Fig. 8Relationship between horizontal stiffness and tr/ts
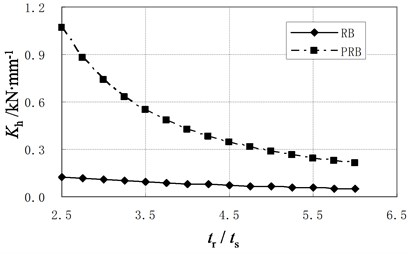
It can be seen from Fig. 8 that the horizontal stiffness of both RB and PRB decreases with the increase of rubber layer’s relative thickness. And the stiffness variation of PRB is much larger than RB. The main reason is that the vertical stiffness of rubber layer is reduced when the thickness of rubber layer increases. Because the vertical stiffness has little effect on the horizontal stiffness of conventional RB, the stiffness variation of RB is relatively small. But the vertical stiffness has great effect on the horizontal stiffness of PRB. The small vertical stiffness leads to large value of , which makes the horizontal deformation easier. Hence, the decrease of the PRB’s horizontal stiffness becomes significant.
3.2.4. Experimental test
The horizontal monotonic load tests are conducted to verify the theoretical derivation. The experimental setup is shown in Fig. 9. The specimens group of PRB4 and PRB5 which were used in vertical loading test are adopted in this experiment. The vertical load is 40 kN, and the prestress force for PRB4 and PRB5 are 50 kN and 30 kN respectively. The experimental results and theoretical curves of lateral force-displacement are compared in Fig. 10. In the theoretical computation, the vertical stiffness is calculated by using Lindley’s formula and the proposed formula respectively.
Fig. 9Experimental setup of horizontal loading
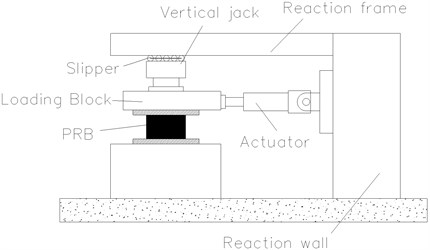
(a) Sketch of experimental setup

(b) Experimental site
Fig. 10Relationship between horizontal force and displacement
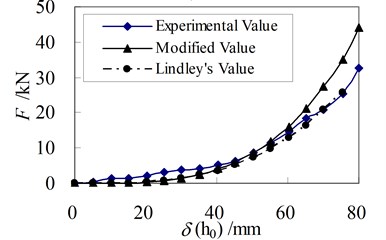
(a) PRB-4 ( 40 kN)
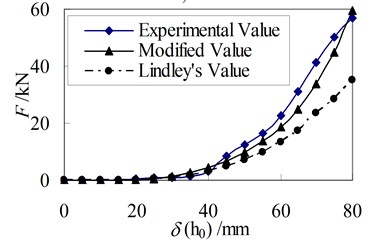
(b) PRB-5 ( 40 kN)
It can be seen that the lateral force obtained from three methods are close to each other when the displacement is small. But the difference between the value of Lindley formula and test result increases gradually when the displacement increases. The difference in PRB-5 is about 60 % of the value from Lindley formula when the horizontal displacement reaches 80 mm. This indicates that the vertical stiffness has large influence on the horizontal stiffness of PRB. The greater the vertical stiffness is, the greater the horizontal stiffness will be. Moreover, this influence increases as horizontal displacement increases. It is due to the coupling relationship between the vertical displacement and horizontal displacement in PRB. A larger horizontal displacement needs a larger vertical displacement. So the larger vertical stiffness leads to a larger horizontal stiffness.
4. Isolation capacities
To study the isolation capacity of PRB, the response history analyses of the structures with PRB are conducted. A hypothetical six-story shear type concrete structure with 4 isolator set on the foundation is adopted. The dimension and material proprieties of isolator are the same as PRB4. The mass of stories is: (i) first floor: 2×104 kg; (ii) top floor: 1.0×104 kg; (iii) the other floors: 1.5×104 kg. The lateral shear stiffness of stories is: (i) first floor: 2×104 kN/m; (ii) top floor: 2×104 kN/m; (iii) the other floors: 1.5×104 kN/m. The damping ratios of structure and isolators are 0.05 and 0.2 respectively.
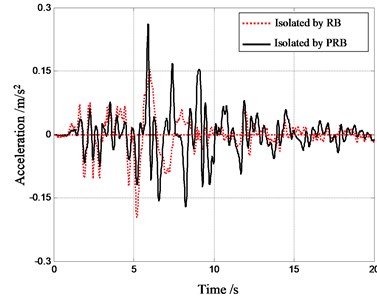
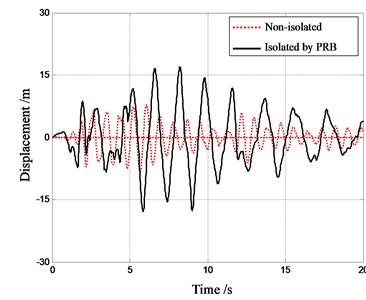
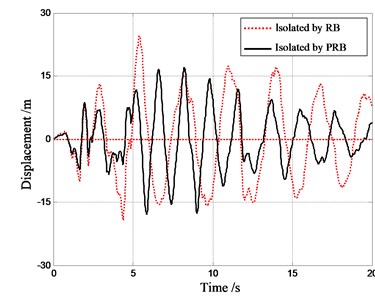
The recorded ground motion (north-south component) in the El-Centro earthquake is adopted as the excitation for the response history analysis. This excitation is scaled so that the peak ground acceleration (PGA) is equal to 0.1 g. Employing the Newmark- integration method [14], the structural responses are computed for 3 different structures: (i) the structure without any isolators; (ii) the structure with conventional RBs; (iii) the structure with PRBs. The acceleration and displacement response history of top-floor are shown in Figs. 11-12.
Fig. 11Acceleration response history of top floor
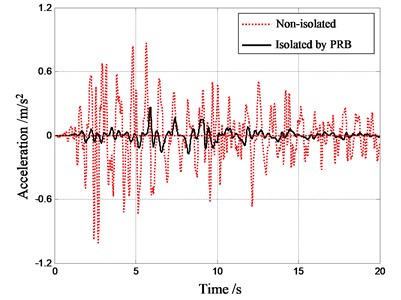
(a) Comparison of structure with PRBs
(b) Comparison of structure with PRBs
Fig. 12Displacement response history of top floor
(a) Comparison of structure with PRBs
(b) Comparison of structure with PRBs
It can be seen that the peak accelerations in top floor of structures with PRBs and with RBs are 0.261 m/s2 and 0.196 m/s2 respectively. The peak acceleration in top floor of non-isolated structure is 1.021 m/s2. Hence both bearings have effective isolation capacity. The peak acceleration in structure with PRB is about 20 % larger than that in structure with RB. So the isolation capacity of PRB is slightly weaker than that of RB. On the other hand, the peak displacement in structure with PRBs is about 40 % smaller than that in structure with RB. The reduction of horizontal displacement is mainly due to the fact that the horizontal stiffness of PRB increases with the increase of horizontal displacement. The large stiffness can limit the further deformation of PRB when the horizontal displacement becomes large. Hence, it can be said that the PRB not only has effective capacity of isolation as conventional RB, but also has sound capacity of horizontal displacement limitation.
To study the influence of seismic intensity on the isolation capacity, the input ground motions are scaled so that the PGAs of motions are equal to 0.2 g and 0.4 g respectively. These two ground excitations correspond to seismic intensity of 8 degree and 9 degree in Chinese Code. The relationships between peak response quantity and excitation intensity are computed and shown in Figs. 13-14.
Fig. 13Relationship between peak acceleration in top floor and excitation intensity
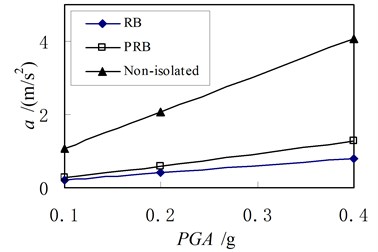
Fig. 14Relation between peak displacement in top floor and excitation intensity
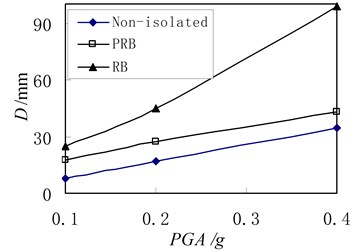
It can be seen from Fig. 13 that the peak accelerations in structures with bearings are similar when the PGA of ground motion is low. Although the peak accelerations in two structures with bearings are different, the difference is not significant. They are both much smaller than the peak acceleration in the non-isolated structure. Therefore, it can be said that the PRB has the similar capacity of isolation as the conventional RB.
Fig. 14 shows that the peak displacements in three structures are small when the ground motion intensity is small. They are increased as the PGAs of ground motions increase. The peak displacement in the structure with PRBs is significantly different from the structure with RBs. The peak displacement in structure with PRBs is close to the displacement in the non-isolated structure. The main reason is that the internal forces of the tendons increase when the horizontal displacement of the bearing increases. The horizontal component of the internal forces can resist most part of the horizontal load and limit the displacement. Therefore, PRB has the capacity of horizontal displacement limitation, and the capacity increases as the PGA of ground motion increases.
5. Conclusions
The following conclusions can be drawn:
1) The Lindley formula was developed base on the conventional RBs with thin rubber layers. It underestimates the vertical stiffness of bearings with thick rubber layers. A modified formula for vertical stiffness of bearings with thick rubber layers is proposed in this paper. Because the suggested modifying coefficient is based on the regression analysis of experimental results, it can only be applied to similar bearings of this paper.
2) Different from the conventional RB, the horizontal stiffness of PRB is variable. The initial stiffness of PRB is close to RB, but it increases with the increase of horizontal displacement. From the numerical investigation, it can be seen that the PRB has effective isolation capacity as the convention RB during earthquake.
3) Due to the existing of prestress tendons, the PRB has the capacity of horizontal displacement limitation. This limitation capacity increases as the PGA of ground motion increases.
References
-
Zhou F. L. Reduction and Control of Structural Vibration. Beijing, Seismology Press, 1997.
-
Iizuka M. A macroscopic model for prediction large deformation behaviors of laminated rubber bearings. Engineering Structures, Vol. 22, 2001, p. 323-334.
-
Kang B. S., Kang G. J., Moon B. Y. Hole and lead plug effect on fiber reinforced elastomeric isolator for seismic isolation. Journal of Materials Processing Technology, Vol. 140, 2003, p. 592-597.
-
Ismail M., Rodellar J., Ikhouane F. An innovative isolation device for aseismic design. Engineering Structures, Vol. 32, 2009, p. 345-356.
-
Kasalanati A., Constantinou M. C. Testing and modeling of prestressed isolators. Journal of Structural Engineering ASCE, Vol. 131, Issue 6, 2005, p. 857-866.
-
Peng T. B., Li J. Z., Fan L. C. Analysis of vertical displacement of double spherical aseismic bearing. Journal of Tongji University: Natural Science Edition, Vol. 35, Issue 9, 2009, p. 1181-1185, (in Chinese).
-
Zhou X. Y., Han M., Zeng D. M., Fan S. R. Rubber bearing isolation system with soft landing protection. Journal of Building Structures, Vol. 21, Issue 5, 2000, p. 2-9, (in Chinese).
-
Cui Y. B., Zhang F. Y. Study on fundamental characteristics of rubber insulation bearing with a steel bar inside. Journal of Hehai University, Vol. 35, Issue 3, 2007, p. 302-305, (in Chinese).
-
Zhang Y. S., Yan X. Y., Wang H., Wei L. S., Zhao G. F. Experimental study on mechanical properties of three-dimensional base isolation and overturn resistance device. Engineering Mechanics, Vol. 26, Issue 1, 2009, p. 124-126, (in Chinese).
-
Wei L. S., Zhou F. L. Application of three-dimensional seismic and vibration isolator to building and site test. Journal of Earthquake Engineering and Engineering Vibration, Vol. 27, Issue 3, 2007, p. 121-125, (in Chinese).
-
Lindley P. B. Natural rubber structural bearings. Joint Sealing and Bearing System for Concrete Structures, Detroit, ACI, 1981, p. 353-378.
-
Gent A. N. Electric stability of rubber compression springs. Journal of Mechanical Engineering Science, Vol. 6, Issue 4, 1964, p. 318-326.
-
Zhou X. Y., Ma D. H., Zeng D. M. A practical computation method for horizontal rigidity coefficient of seismic isolation rubber bearing. Building Science, Vol. 14, Issue 6, 1998, p. 3-8, (in Chinese).
-
Chopra A. K. Dynamics of Structures: Theory and Applications to Earthquake Engineering. London, Pearson Education, 2005.
About this article
This work was financially supported by the National Science Foundation of China under Grant No. 51108091.
