Abstract
Magnetic memory testing is a new nondestructive testing technology, which can detect the early damage of ferromagnetic components such as stress concentration. In this paper, the coupling model between the stress of ferromagnetic material and its magnetic leakage field is established. In this model, the relative change rate of permeability of ferromagnetic material is proportional to the stress, the change of permeability and the saturation magnetic induction. The experimental results show that the model can well describe the relationship between stress and leakage magnetic field.
1. Introduction
Metal magnetic memory detection is referred to as magnetic memory detection. It is a new non-destructive testing technology which appeared in recent decades, which was first proposed by Russian scholar Dubov [1-3]. Compared with the traditional nondestructive testing technology, magnetic memory testing has incomparable advantages. Traditional nondestructive testing techniques, such as ultrasonic testing, radiographic testing, magnetic particle testing and eddy current testing, can detect the macro defects and most of the micro defects. But for the early damage of ferromagnetic materials, especially the discontinuous, undeveloped and hidden damage, it is powerless. While by detecting the weak magnetic field emitted by the ferromagnetic component itself, the magnetic memory detection technology can find the location of stress concentration, that is, the location of early damage.
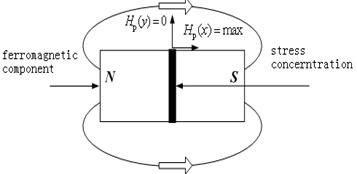
The principle of magnetic memory testing can be described as follows. As shown in Fig. 1, under the combined action of the earth's magnetic field and external load, ferromagnetic materials will have a kind of magnetostrictive reorientation. This orientation is directional and irreversible. Ferromagnetic materials will produce the largest change of leakage magnetic field in the stress and deformation position. At this position, the tangential component of the leakage magnetic field has a maximum, while the normal component changes sign and has a zero point. This irreversible change will not disappear due to the elimination of external load. At this time, by measuring the normal component of leakage magnetic field and calculating its gradient value, the stress concentration position of ferromagnetic material can be determined.
Fig. 1Schematic diagram of metal magnetic memory testing principle
2. The relationship between the quantification of magnetic memory testing and the magneto mechanical coupling model
Because the mechanism of magnetic memory testing is not clear, magnetic memory testing technology can only detect the stress concentration position of ferromagnetic materials, and can not quantify the early damage. For ferromagnetic equipment, quantifying early damage is not only the premise of taking correct maintenance measures, but also the important basis of predicting the remaining life of equipment. In other words, it is easy to waste to replace the equipment or components too early, and it may lead to accidents to take maintenance measures too late. Therefore, the quantitative study of early damage is very necessary, and it has become a key scientific and technological problem restricting the development and application of magnetic memory testing technology. Because the research work of magnetic memory technology mainly comes from engineering practice and lacks systematic mechanism research and experimental verification, the micro mechanism of magnetic memory detection has not yet formed a systematic theoretical system. The complex coupling relationship between stress concentration and magnetic flux leakage (MFL) is not fully clear, and the complex nonlinear relationship between stress concentration, MFL and magnetic memory (MMM) signal is even more difficult to establish [4-6], which leads to fact that the magnetic memory technology can not quantify the early damage identification. Therefore, it is very important to establish a correct mechanical magnetic coupling model, which is the basis of magnetic memory testing research [7-10].
From the current research situation at home and abroad, it can be seen that magnetic memory method can be used in the detection and evaluation of early damage or defect of ferromagnetic materials, and the researchers have explored the method of magnetic memory for the detection and evaluation of early damage or defect of ferromagnetic materials [11-19]. Because the micro mechanism of magnetic memory testing is complex, the existing force magnetic coupling model has its own defects, which cannot accurately describe the force magnetic coupling effect. In quantifying the early damage or defect of ferromagnetic materials and analyzing the complex relationship between stress-strain and magnetic memory signal, uniaxial and biaxial tensile tests or fatigue tests under various typical loads are mainly used, which is used to analyze the qualitative relationship between the mean stress and the magnetic memory signal. A large number of experimental statistical data can fit the quantitative relationship between magnetic field signal and stress from a macro point of view. But this kind of experiment can't reflect the real size of stress, especially the real situation of stress concentration. In addition, the problem of extracting the characteristic parameters of the magnetic memory signal corresponding to the early damage has not been solved effectively. So far, it is impossible to establish an effective relationship model among stress concentration, magnetic flux leakage and magnetic memory signal. Therefore, it is impossible to fully reveal the inherent law between the early damage of ferromagnetic materials and the magnetic memory signal, and naturally it is impossible to make an accurate quantitative assessment of the early damage of equipment or components. The coupling relationship between the structure of internal stress and strain fields and their spatial magnetic memory characteristics should be clarified first. On this basis, the real bearing environment of equipment or components in actual service is further simulated, and the complex nonlinear relationship between stress concentration and magnetic memory signal is explored from micro and macro perspectives, so as to realize the quantification of magnetic memory stress detection.
3. A new mechanical and magnetic coupling model
The experimental results show that above Curie temperature, the ferromagnetic material satisfies Curie Weiss law, that is, the magnetic susceptibility . The relationship between magnetic field strength and magnetic intensity is given by Eq. (1):
where, represents the Curie temperature of ferromagnetic materials, represents the absolute temperature, and represents the Curie constant. It can be seen from Eq. (1) that there is an additional field in ferromagnetic materials , which is called molecular field. The molecular field and external magnetic field act on the atomic magnetic moment together. The relationship between them is given by Eq. (2):
where, is the additional molecular field, represents the molecular field parameter. Therefore, the effective field in ferromagnetic material is given by Eq. (3):
The effective field in Eq. (3) is the leakage magnetic field distributed on the surface of ferromagnet with defects, which is also the variable described in the principle of magnetic memory testing. The stress concentration of ferromagnetic materials can be determined by measuring the normal component and tangential component of the leakage magnetic field .
When the elastic stress acts on the ferromagnetic component, the ferromagnet will produce not only elastic strain, but also magnetostrictive strain, which will cause the displacement of the domain wall and change the direction of spontaneous magnetization. This phenomenon is usually called magnetoelastic effect or force - induced expansion. The magnetoelastic effect is due to the close relationship between the domain structure and the stress state. The ferromagnet will increase the stress energy in the magnetic crystal when it is stressed. According to the principle of the actual state of existence must be the state of minimum energy, only by reducing the stress energy to the minimum, can the ferromagnet be in a new stable state. The way to reduce the stress energy is to change the direction of magnetization. When there is external stress, for isotropic and positive magnetostrictive materials, the direction of magnetization tends to the direction of tensile force when tensile force is applied. On the contrary, the direction of magnetization tends to be perpendicular to the direction of tensile force. Therefore, ferromagnetic materials will reorient the magnetization vector under the action of stress, thus changing the permeability in the direction of stress. According to the basic theory of ferromagnetism, a magnetomechanical coupling model of the relationship between relative permeability and stress of ferromagnetic materials is established [3]. The Coupling model is given by Eq. (4):
where, is the permeability of ferromagnetic material, is the environment variable, is the coefficients related to ferromagnetic materials, is the saturated magnetostrictive coefficient of ferromagnetic materials, is the change of permeability of ferromagnetic materials, is the Saturation magnetic induction of ferromagnetic materials, is the stress of ferromagnetic materials. The Eq. (4) shows that the following relationship holds. Firstly, the relative permeability change rate and of ferromagnetic materials are proportional. Secondly, with the increase of saturation magnetic induction , changes proportionally. Thirdly, with the increase of saturation magnetostrictive coefficient , also changes in proportion.
4. Experimental verification of magnetomechanical coupling model
In this paper, the magnetic memory test of ferromagnetic specimen under external tensile load is carried out to verify the correctness of the force magnetic coupling model.
4.1. Experimental equipment and materials
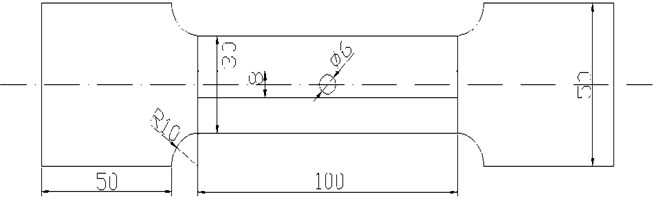
The experimental instruments are MFL-4032 MFL/MMM detector and MTS810 hydraulic servo testing machine, as shown in Fig. 2 and Fig. 3. The static load error of MTS810 hydraulic servo testing machine is ±0.5 %, and the dynamic load error is ± 1 %. MFL-4032 MFL/MMM detector is an experimental instrument for detecting the magnetic leakage field of ferromagnetic materials. The ferromagnetic material used in the experiment is Q235 steel, and its mechanical properties are shown in Table 1. The Q235 steel specimen is processed into the shape shown in Fig. 4. The thickness of the specimen is 4mm and the diameter of the central hole is 6 mm. The horizontal straight line below the central circular hole of the specimen is the measuring line for magnetic memory testing, which is 4mm away from the center of the circular hole.
Table 1Performance of Q235
Type | Tensile strength (MPa) | Yield strength (MPa) |
Q235 | 235 | 375-460 |
Fig. 2MTS810 hydraulic servo testing machine

Fig. 3MFL-4032 MFL/MMM detector

Fig. 4Specimen
4.2. Experimental process
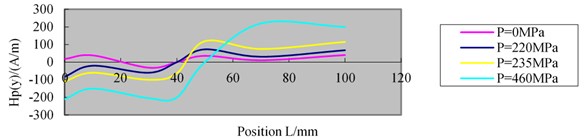
During the experiment, in order to avoid the interference of metal clamping device on the signal, a non-magnetic clamping device was used to clamp the magnetic memory detector probe of mfl-4032 magnetic flux leakage / magnetic memory detector. The magnetic memory testing probe is perpendicular to the specimen to be tested, and the lifting height of the magnetic memory testing probe is 0.5 mm. The clamping device advances along the detection line as shown in Fig. 2 at a fixed speed. The magnetic memory signal on the surface of the specimen in the initial state was measured. When the tensile stress of the specimen reaches 220 MPa, 235 MPa and 460 MPa respectively, the magnetic memory signal on the surface of the specimen is collected. In order to improve the reliability and accuracy of the test data, each group of data were repeated for 10 times, and the average value was taken as the final result of the group of data (as shown in Fig. 5).
Fig. 5MMMT signals measured under tension load
4.3. Analysis of experimental results
The following results can be seen from the experimental curve in Fig. 5. Before the specimen is loaded, the magnetic memory signal is very weak, and there are two zero crossing points in the magnetic memory signal curve. When the tensile stress is 220 MPa, the specimen is in the stage of elastic deformation. Under the combined action of tensile load and geomagnetic field, the ferromagnetic specimen produces obvious stress concentration in the central hole. The amplitude of magnetic memory signal begins to increase, and the curve of magnetic memory signal has a zero-crossing point, which is not far from the center. When the tensile stress is 235 MPa, the specimen begins to yield. The amplitude of the magnetic memory signal increases significantly, and the zero-crossing point of the magnetic memory signal curve tends to be close to the center of the specimen. When the tensile stress of the specimen is 460 MPa, the tensile stress exceeds the strength limit of the specimen. The plastic deformation and fracture occurred in the center of the specimen. After closing the fractured specimen and measuring the magnetic leakage field on its surface, the following results can be found. At this time, the amplitude of the magnetic memory signal obviously exceeds the previous amplitude. The zero-crossing position of the magnetic memory signal curve is located at the fracture of the specimen, and the amplitude of the magnetic memory signal at the zero crossing position of the curve is the largest.
According to Eq. (4), the relative permeability change is calculated when the tensile stress is 220 MPa, 235 MPa and 460 MPa respectively. It can be found that the tensile stress is consistent with the magnetic memory signal. In other words, the coupling model can well describe the relationship between ferromagnetic material stress and leakage magnetic field.
5. Conclusions
In view of the shortcomings of the existing magnetic coupling model of magnetic memory, a new magnetic coupling model of magnetic memory is established based on the principle of minimum energy in the basic theory of ferromagnetism. relationship between relative permeability and stress of ferromagnetic materials is given by the equation . In the Eq. (4), is the permeability of ferromagnetic material, is the environment variable, is the coefficients related to ferromagnetic materials, is the saturated magnetostrictive coefficient of ferromagnetic materials, is the change of permeability of ferromagnetic materials, is the Saturation magnetic induction of ferromagnetic materials. The correctness of the model is verified by the tensile test in this paper.
References
-
Dubov A. A. A study of metal properties using the method of magnetic memory. Metal Science and Heat Treatment, Vol. 39, Issue 9, 1997, p. 401-402.
-
Dubov A. Principle features of metal magnetic memory method and inspection tools as compared to known magnetic NDT methods. CINDE Journal, Vol. 27, Issue 3, 2006, p. 16-20.
-
Dubov A. Diagnostics of metal items and equipment by means of metal magnetic memory proc of CHSNDT. Proceeding of CHSNDT 7th Conference on NDT and International Research Symposium, Guangzhou, China, 1999, p. 181-187.
-
Xu Mingxiu, Chen Zhanghua, Xu Minqiang, Fan Jiuming Mechanism of magnetic memory signal variation in the process of fatigue. Journal of Mechanical Engineering, Vol. 50, Issue 4, 2014, p. 53-59.
-
Bai Yong, Xu Fan, Qiao Aitong Relationship between residual plastic deformation and metal magnetic memory signals of specimens. Journal of Materials Engineering, Vol. 49, Issue 8, 2013, p. 42-49.
-
Shi Pengpeng, Hao Shuai Analytical solution of magneto-mechanical magnetic dipolemodel for metal magnetic memory method. Acta Physica Sinica, Vol. 70, Issue 3, 2021, p. 034101.
-
Cullity B. D., Graham C. D. Introduction to Magnetic Materials. IEEE Press, New Jersey, 2009.
-
Jiles D. C., Atherton D. L. Theory of the magnetization process in ferromagnets and its application to the magneto mechanical effect. Journal of Physics D-Applied Physics, Vol. 17, Issue 6, 1984, p. 1275-1281.
-
Jiles D. C. Theory of the magneto mechanical effect. Journal of Physics D-Applied Physics, Vol. 28, Issue 8, 1995, p. 1537-1546.
-
Li L., Jiles D. C. Modeling of the magneto mechanical effect: application of the Rayleigh law to the stress domain. Journal of Applied Physics, Vol. 93, Issue 10, 2003, p. 8480-8482.
-
Kuleev V. G. Magetization distribution over long ferromagnetic steel pipes in a weak external magnetic field under elastic and plastic bending. Russian Journal of Nondestructive Testing, Vol. 38, Issue 6, 2002, p. 452-464.
-
Wilson J. W., Tian G. Y., Barrans S. Residual magnetic field sensing for stress measurement. Sensors and Actuators A: Physical, Vol. 135, Issue 2, 2007, p. 381-387.
-
Roskosz M., Bieniek M. Evaluation of residual stress in ferromagnetic steels based on residual magnetic field measurements. NDT&E International, Vol. 45, Issue 1, 2012, p. 55-62.
-
Dubov A. A. Evaluation of service life of equipment using magnetic memory method. Tyazheloe Mashinostroenie, Vol. 6, 2005, p. 13-15.
-
Huang Songling, Li Luming, Wang Laifu, Liu Shifeng Stress distribution testing by metal magnetic memory method. Nondestructive Testing, Vol. 24, Issue 5, 2002, p. 212-214.
-
Ding Hui, Zhang Han, Li Xiaohong, Wen Xishan The theoretical model for detecting cracks by metal magnetic memory technique. Nondestructive Testing, Vol. 24, Issue 2, 2002, p. 78-80.
-
Liu Shujun, Li Zhuxin, Su Yi Metal magnetic memory testing of X60 pipeline steel under tension load and fatigue load. Applied Mechanics and Materials, Vol. 148, Issue 149, 2012, p. 1404-1407.
-
Chen Shangong, Zong Xuemei, Huang Haihong, Wang Guangcun, He Bing Fatigue damage evaluation of used parts based on metal magnetic memory testing. Nondestructive Testing, Vol. 43, Issue 1, 2021, p. 29-33.
-
Zhang Shaochun, Pang Hongchen, Liao Kexi Non-contact magnetic detection of mountain small-diameter pipelines. Nondestructive Testing, Vol. 43, Issue 2, 2021, p. 16-20.
