Abstract
Multiple earthquake damages show that the long-period ground movements have an amplification effect on the dynamic response and seismic damage of long-period structures. To form an improved code design spectrum suitable for long-period ground movements, the standard response spectra consisting of four segments for near-fault pulse-like (NFPL) and far-field harmonic (FFH) ground movements are proposed. Firstly, two types of special long-period ground movements with reliable information are selected for this research. Then, the fundamental period of a single-degree-of-freedom (SDOF) system is extended to 16 s with the damping ratio of 5 %, and the seismic response spectrum and the normalized response spectrum are analyzed. Next, the normalized acceleration spectrum of long-period ground movements is calibrated to the standard response spectrum of regular variation. Finally, the parameters of standard response spectrum about long-period ground movements and the ones of the current code design spectrum are discussed. The results show that the current code design spectrum overestimates the structural seismic response in the short period under NFPL and FFH ground movements, while it underestimates the structural seismic response in the long period. The fundamental period of a SDOF system of china’s current code design spectrum should be extended to consider the influence on long-period structures acted by a long-period earthquake. Further, it accounts for the resonance effect of long-period ground movements which ensures the seismic design safety of long-period structures.
1. Introduction
The database expansion of recording ground movements demonstrates that there is significant long-period components lying in recent great earthquakes, such as Wenchuan earthquake, Chi-Chi earthquake, Great East Japan earthquake, and so on [1-5]. Near-fault pulse-like (NFPL) ground movements and far-field harmonic (FFH) ground movements are currently known as two types of classical long-period ground movements [6]. The increasing long-period structures will undoubtedly be damaged by long-period ground movements in the future, and the seismic behaviors of such long-period structures are worthy of further and extensive researches [7-13]. The resonant effect on long-period structures acted by long-period ground movements has already attracted wide attention from seismology and engineering scholars [14-16].
Compared with the time history analysis, the response spectrum analysis can present the three-element properties of ground movements. Among them, the platform value of response spectrum can reflect the peak characteristics of ground movements, and the characteristic period of response spectrum can reflect the spectrum characteristics of ground movements.
The selected value of long-period segment of seismic design spectrum plays an important role in the seismic design of long-period structures. In recent years, Digital Seismograph has created many strong earthquake records with reliable long-period components, and many researchers have discussed the reasonable value of long-period segment [17, 18]. Geng et al., who analyzed the provisions for decline segment about seismic design spectrum by counting strong earthquake records, thought the value of long-period segment was too conservative [19]. In the 1-6 s period, the decline of design response spectrum by the rate of is sufficiently secure, and it was suggested to extend to 10 s. Zhou et al., who studied the value of the long-period segment of seismic design spectrum by collecting high-quality acceleration records and related data in different regions, suggested the long-period segment of design response spectrum should not be segmented and the attenuation index should be taken as 0.9 [20]. At the same time, the characteristic periods of design response spectra in various site classifications should be appropriately amplified. The magnitude of a seismic event, source-to-site distance and site condition are generally considered as the main factors influencing the shape of response spectrum, and the seismic design spectrum in the current code has taken into account the influence of magnitude, distance and site type.
Firstly, a typical 189 long-period and 26 common earthquake records with reliable information are selected for this study. Then, various kinds of response spectrum are studied based on the response spectrum theory. Moreover, the statistical response spectra of long-period ground movements are compared with code design spectrum, so as to provide a reference for seismic response analysis of long-period structures and value revision of long-period segment about code design spectrum in China.
2. Selection of long-period ground movements
According to the inherent characteristics and selection principle of long-period ground movements [21-23], 89 NFPL ground movements and 100 FFH ground movements are considered as long-period ground movements for this study. And 26 common ground movements are employed for comprehensive comparison analysis with long-period ground movements. Tables 1-3 demonstrate the specific information of NFPL, FFH and common ground movements, respectively.
3. Response spectrum characteristics of long-period ground movements
Seismic response spectra include acceleration, velocity and displacement spectrum, while in the normalized response spectra (also known as magnification factor spectra), the acceleration, velocity and displacement spectrum are normalized. The velocity time history of long-period ground movements can be obtained by integrating the acceleration time history, while the displacement time history of long-period ground movements can be obtained by integrating the velocity time history. Original acceleration amplitude is adopted to calculate the seismic response spectra of ground movements, yet the acceleration amplitude is scaled to 1 cm/s2 for the normalized response spectra. The normalized acceleration amplitude can eliminate the influence on the ordinate value of response spectra by earthquake intensity, and it also can reflect the response amplification of a single-degree-of-freedom (SDOF) system under earthquake excitation. These kinds of response spectra under three types of earthquake action are calculated respectively. To comprehensively understand the low-frequency characteristics about long-period ground movements, the fundamental period of a SDOF system is extended to 16s with the damping ratio of 5 %.
Table 1Information of NFPL ground movements
Station / component | Site class | Rupture distance | Station / component | Site class | Rupture distance | Station / component | Site class | Rupture distance | |||
TCU104-EW | C | 7.6 | 12.87 | TCU109-NS | C | 7.6 | 13.06 | 1083_GLE260 | C | 6.7 | 13.3 |
TCU104-NS | C | 7.6 | 12.87 | TCU074-EW | C | 7.6 | 13.46 | 1016_NYA090 | C | 6.7 | 18.5 |
TCU068-EW | C | 7.6 | 0.32 | TCU074-NS | C | 7.6 | 13.46 | 1016_NYA180 | C | 6.7 | 18.5 |
TCU068-NS | C | 7.6 | 0.32 | CHY034-EW | C | 7.6 | 14.82 | 1085_SCE018 | C | 6.7 | 5.2 |
TCU052-EW | C | 7.6 | 0.66 | CHY034-NS | C | 7.6 | 14.82 | 1085_SCE288 | C | 6.7 | 5.2 |
TCU052-NS | C | 7.6 | 0.66 | TCU107-EW | C | 7.6 | 15.99 | 1086_SYL090 | C | 6.7 | 5.3 |
CHY080-EW | C | 7.6 | 2.69 | TCU107-NS | C | 7.6 | 15.99 | 1086_SYL360 | C | 6.7 | 5.3 |
CHY080-NS | C | 7.6 | 2.69 | TCU036-EW | C | 7.6 | 19.83 | 1080_KAT000 | C | 6.7 | 13.4 |
TCU120-EW | C | 7.6 | 7.4 | TCU036-NS | C | 7.6 | 19.83 | 1080_KAT090 | C | 6.7 | 13.4 |
CHY006-EW | C | 7.6 | 9.76 | TCU064-EW | C | 7.6 | 16.59 | 1013_LDM064 | C | 6.7 | 5.9 |
CHY006-NS | C | 7.6 | 9.76 | TCU064-NS | C | 7.6 | 16.59 | 1013_LDM334 | C | 6.7 | 5.9 |
TCU063-NS | C | 7.6 | 9.78 | TCU048-EW | C | 7.6 | 13.53 | 953_MUL009 | D | 6.7 | 17.1 |
CHY029-EW | C | 7.6 | 10.96 | TCU048-NS | C | 7.6 | 13.53 | 953_MUL279 | D | 6.7 | 17.1 |
TCU116-EW | C | 7.6 | 12.38 | TCU128-EW | C | 7.6 | 13.13 | 960_LOS000 | D | 6.7 | 12.4 |
TCU116-NS | C | 7.6 | 12.38 | TCU128-NS | C | 7.6 | 13.13 | 960_LOS270 | D | 6.7 | 12.4 |
CHY029-NS | C | 7.6 | 10.96 | CHY104-EW | D | 7.6 | 18.02 | 949_ARL090 | D | 6.7 | 8.7 |
TCU100-NS | C | 7.6 | 11.37 | CHY104-NS | D | 7.6 | 18.02 | 949_ARL360 | D | 6.7 | 8.7 |
TCU138-NS | C | 7.6 | 9.78 | TCU065-EW | D | 7.6 | 0.57 | 1087_TAR090 | D | 6.7 | 15.6 |
TCU063-EW | C | 7.6 | 9.78 | TCU065-NS | D | 7.6 | 0.57 | 1087_TAR360 | D | 6.7 | 15.6 |
TCU102-EW | C | 7.6 | 1.49 | CHY025-EW | D | 7.6 | 19.07 | 1063_RRS228 | D | 6.7 | 6.5 |
TCU102-NS | C | 7.6 | 1.49 | CHY025-NS | D | 7.6 | 19.07 | 1063_RRS318 | D | 6.7 | 6.5 |
TCU136-EW | C | 7.6 | 8.27 | TCU123-EW | D | 7.6 | 14.91 | 1084_SCS052 | D | 6.7 | 5.3 |
TCU136-NS | C | 7.6 | 8.27 | TCU123-NS | D | 7.6 | 14.91 | 1084_SCS142 | D | 6.7 | 5.3 |
TCU103-EW | C | 7.6 | 6.08 | 1050_PAC175 | A | 6.7 | 7 | 1044_NWH090 | D | 6.7 | 5.9 |
TCU087-NS | C | 7.6 | 6.98 | 1050_PAC265 | A | 6.7 | 7 | 1044_NWH360 | D | 6.7 | 5.9 |
TCU039-EW | C | 7.6 | 19.89 | 1012_LA0000 | C | 6.7 | 19.1 | 1045_WPI046 | D | 6.7 | 5.5 |
TCU039-NS | C | 7.6 | 19.89 | 1012_LA0090 | C | 6.7 | 19.1 | 1045_WPI316 | D | 6.7 | 5.5 |
CHY035-EW | C | 7.6 | 12.65 | 1052_PKC090 | C | 6.7 | 7.6 | 1082_RO3000 | D | 6.7 | 10.1 |
CHY035-NS | C | 7.6 | 12.65 | 1052_PKC360 | C | 6.7 | 7.6 | 1082_RO3090 | D | 6.7 | 10.1 |
TCU109-EW | C | 7.6 | 13.06 | 1083_GLE170 | C | 6.7 | 13.3 |
3.1. Acceleration response spectrum
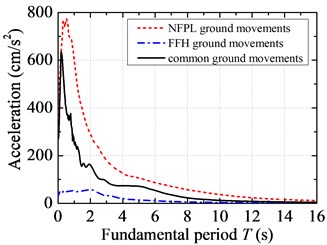
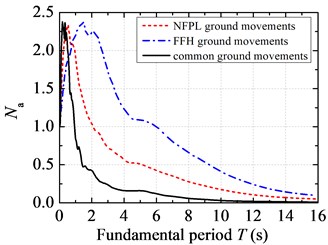
Fig. 1 demonstrates a comparison of acceleration response spectra under three types of earthquake action. The shapes of seismic acceleration spectra under NFPL long-period and common ground movements are close to each other. That is to say, they both experienced three stages: rapid growth → rapid decrease → slow decrease. The increase and decrease of seismic acceleration spectrum under FFH long-period ground movements are relatively slow. When the fundamental period of a SDOF system is beyond 8 s, the acceleration spectrum basically remains unchanged. On the whole, the seismic acceleration spectrum under NFPL long-period ground movements is higher than those under common and FFH long-period ground movements. The peak of acceleration time-history under FFH long-period ground movements attenuates rapidly with the increase of distance, which leads to its low acceleration spectrum. The peaks of the normalized acceleration spectra under common, NFPL and FFH long-period ground movements are close to each other, and they are 2.377, 2.370 and 2.339 respectively. However, the fundamental periods of a SDOF system corresponding to spectrum peaks have significant differences. The normalized acceleration spectrum under common ground movements reaches the peak at 0.18 s, while those under NFPL and FFH long-period ground movements reach the peaks at 0.52 s and 1.48 s respectively. In addition, the normalized acceleration spectra under long-period ground movements are relatively dispersed throughout the fundamental periods, and they are not concentrated in the period range of 1 s as that under common ground movements. When is less than 0.42 s, the normalized acceleration spectra under long-period ground movements are smaller than that under common ground movements. When is beyond 0.56 s, spectra values under long-period ground movements are larger than that under common ground movements.
Table 2Information of NFPL ground movements
Station / component | Site class | Epicenter distance | Station / component | Site class | Epicenter distance | Station / component | Site class | Epicenter distance | |||
GIFH24-EW2 | B | 7.3 | 683 | AIC001-EW | E | 7.3 | 620 | CHBH20-EW2 | A | 9.0 | 416 |
GIFH24-NS2 | B | 7.3 | 683 | AIC001-NS | E | 7.3 | 620 | CHBH20-NS2 | A | 9.0 | 416 |
KYTH04-EW2 | B | 7.3 | 523 | NGNH28-EW2 | B | 8.0 | 763 | SZOH53-EW2 | B | 9.0 | 562 |
KYTH04-NS2 | B | 7.3 | 523 | NGNH28-NS2 | B | 8.0 | 763 | SZOH53-NS2 | B | 9.0 | 562 |
SMNH09-EW2 | C | 7.3 | 233 | FKSH21-EW2 | C | 8.0 | 640 | YMNH13-EW2 | B | 9.0 | 500 |
SMNH09-NS2 | C | 7.3 | 233 | FKSH21-NS2 | C | 8.0 | 640 | YMNH13-NS2 | B | 9.0 | 500 |
MIEH03-EW2 | C | 7.3 | 557 | AOM018-EW | C | 8.0 | 343 | ABSH01-EW2 | B | 9.0 | 714 |
MIEH03-NS2 | C | 7.3 | 557 | AOM018-NS | C | 8.0 | 343 | ABSH01-NS2 | B | 9.0 | 714 |
NAR007-EW | C | 7.3 | 490 | ABSH04-EW2 | C | 8.0 | 280 | YMTH12-EW2 | C | 9.0 | 256 |
NAR007-NS | C | 7.3 | 490 | ABSH04-NS2 | C | 8.0 | 280 | YMTH12-NS2 | C | 9.0 | 256 |
KOCH13-EW2 | C | 7.3 | 285 | NIGH11-EW2 | C | 8.0 | 687 | YMN010-EW | C | 9.0 | 472 |
KOCH13-NS2 | C | 7.3 | 285 | NIGH11-NS2 | C | 8.0 | 687 | YMN010-NS | C | 9.0 | 472 |
MIEH07-EW2 | C | 7.3 | 587 | HKD130-EW | C | 8.0 | 241 | NIGH17-EW2 | C | 9.0 | 443 |
MIEH07-NS2 | C | 7.3 | 587 | HKD130-NS | C | 8.0 | 241 | NIGH17-NS2 | C | 9.0 | 443 |
OKYH06-EW2 | C | 7.3 | 333 | AKT013-EW | C | 8.0 | 399 | YMT002-EW | D | 9.0 | 236 |
OKYH06-NS2 | C | 7.3 | 333 | AKT013-NS | C | 8.0 | 399 | YMT002-NS | D | 9.0 | 236 |
HRS004-EW | C | 7.3 | 260 | YMTH14-EW2 | D | 8.0 | 513 | HKD102-EW | D | 9.0 | 531 |
HRS004-NS | C | 7.3 | 260 | YMTH14-NS2 | D | 8.0 | 513 | HKD102-NS | D | 9.0 | 531 |
OSK010-EW | D | 7.3 | 454 | HKD025-EW | D | 8.0 | 374 | HKD030-EW | D | 9.0 | 676 |
OSK010-NS | D | 7.3 | 454 | HKD025-NS | D | 8.0 | 374 | HKD030-NS | D | 9.0 | 676 |
AIC015-EW | D | 7.3 | 654 | HKD151-EW | D | 8.0 | 318 | AOMH10-EW2 | D | 9.0 | 336 |
AIC015-NS | D | 7.3 | 654 | HKD151-NS | D | 8.0 | 318 | AOMH10-NS2 | D | 9.0 | 336 |
TTR006-EW | D | 7.3 | 404 | AKT018-EW | D | 8.0 | 437 | FKSH03-EW2 | D | 9.0 | 279 |
TTR006-NS | D | 7.3 | 404 | AKT018-NS | D | 8.0 | 437 | FKSH03-NS2 | D | 9.0 | 279 |
NGN024-EW | D | 7.3 | 721 | MYG005-EW | D | 9.0 | 208 | AIC005-EW | D | 9.0 | 599 |
NGN024-NS | D | 7.3 | 721 | MYG005-NS | D | 9.0 | 208 | AIC005-NS | D | 9.0 | 599 |
TKS005-EW | D | 7.3 | 360 | YMT001-EW | E | 8.0 | 482 | AOM019-EW | E | 9.0 | 366 |
TKS005-NS | D | 7.3 | 360 | YMT001-NS | E | 8.0 | 482 | AOM019-NS | E | 9.0 | 366 |
EHM016-EW | D | 7.3 | 213 | FKS020-EW | E | 8.0 | 580 | AIC003-EW | E | 9.0 | 636 |
EHM016-NS | D | 7.3 | 213 | FKS020-NS | E | 8.0 | 580 | AIC003-NS | E | 9.0 | 636 |
EHMH04-EW2 | D | 7.3 | 249 | YMT015-EW | E | 8.0 | 548 | NIG009-EW | E | 9.0 | 310 |
EHMH04-NS2 | D | 7.3 | 249 | YMT015-NS | E | 8.0 | 548 | NIG009-NS | E | 9.0 | 310 |
EHMH07-EW2 | D | 7.3 | 203 | IUBH03-EW | E | 8.0 | 206 | ||||
EHMH07-NS2 | D | 7.3 | 203 | IUBH03-NS | E | 8.0 | 206 |
3.2. Velocity response spectrum
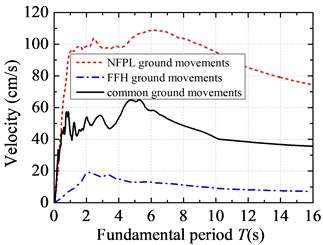
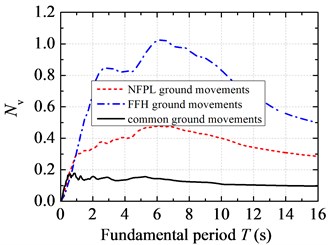
Fig. 2 illustrates a comparison of velocity response spectra under three types of earthquake action. The shapes of seismic velocity spectra under long-period and common ground movements are close to each other. That is to say, they all experienced two stages: rapid growth → slow decrease. On the whole, the seismic velocity spectrum under NFPL long-period ground movements is higher than those under common and FFH long-period ground movements. The peak of acceleration time-history under FFH long-period ground movements attenuates rapidly with the increase of distance, which leads to the low integral velocity spectrum. When is beyond 1.0 s, seismic velocity spectrum under NFPL long-period ground movements is about 2 times of that under common ground movements, while the spectrum under FFH long-period ground movements is only half of that under common ground movements. When is less than 0.8 s, the normalized velocity spectra under long-period ground movements are similar to that under common ground movements. When is beyond 0.8 s, spectra values under long-period ground movements are larger than that under common ground movements. The fundamental periods corresponding to the peaks of velocity spectra under long-period ground movements are obviously larger than that under common ground movements. The normalized velocity spectrum under common ground movements reaches the peak at 0.88 s, while those under NFPL and FFH long-period ground movements reach the peaks at 6.14 s and 6.36 s respectively.
Table 3Information of common ground movements
Station / component | Site class | Rupture distance | Station / component | Site class | Rupture distance | Station / component | Site class | Rupture distance | |||
TAB-L1 | B | 7.35 | 2.05 | HCH180 | D | 6.93 | 27.6 | SHI000 | D | 6.9 | 19.15 |
TAB-T1 | B | 7.35 | 2.05 | ELC180 | D | 6.59 | 6.09 | SHI090 | D | 6.9 | 19.15 |
PAS180 | C | 7.36 | 125.59 | ELC270 | D | 6.59 | 6.09 | B-WSM090 | D | 6.54 | 13.03 |
PAS270 | C | 7.36 | 125.59 | ELC000 | D | 5.0 | 34.98 | B-WSM180 | D | 6.54 | 13.03 |
OKA000 | C | 6.9 | 86.94 | ELC090 | D | 5.0 | 34.98 | B-ICC000 | D | 6.54 | 18.2 |
OKA090 | C | 6.9 | 86.94 | AGW000 | D | 6.93 | 24.57 | B-ICC090 | D | 6.54 | 18.2 |
TAF021 | C | 7.36 | 38.89 | AGW090 | D | 6.93 | 24.57 | B-IVW090 | E | 6.54 | 23.85 |
TAF111 | C | 7.36 | 38.89 | OSA000 | D | 6.9 | 21.35 | B-IVW360 | E | 6.54 | 23.85 |
HCH090 | D | 6.93 | 27.6 | OSA090 | D | 6.9 | 21.35 |
Fig. 1Acceleration response spectra
a) Seismic acceleration spectra
b) Normalized acceleration spectra
Fig. 2Velocity response spectra
a) Seismic velocity spectra
b) Normalized velocity spectra
3.3. Displacement response spectrum
Fig. 3 demonstrates a comparison of displacement response spectra under three types of earthquake action. The shapes of seismic displacement spectra under NFPL long-period ground movements and common ground movements are close to each other. That is to say, they both experienced two stages: rapid growth → slow decrease. The seismic displacement spectrum under FFH long-period ground movements changes slightly with the increase of fundamental period. It increases slowly when is less than 4.0 s and remains unchanged after 4.0 s. The peak of acceleration time-history under FFH long-period ground movements attenuates rapidly with the increase of distance, which leads to a low value of quadratic-integral displacement spectrum. On the whole, the seismic displacement spectrum under NFPL long-period ground movements is higher than those under common and FFH long-period ground movements. When is less than 8.88 s, seismic displacement spectrum under NFPL long-period ground movements increases rapidly with the increase of fundamental period. And it is about 2.8 and 9.9 times of those under common and FFH long-period ground movements after 8.88 s. When is less than 0.56 s, the normalized displacement spectra under long-period ground movements are similar to that under common ground movements. When is beyond 0.56 s, the spectra under long-period ground movements are larger than that under common ground movements. The normalized displacement spectrum under FFH long-period ground movements is larger than that under NFPL long-period ground movements. The normalized displacement spectrum under FFH long-period ground movements increases rapidly when is less than 8.82 s and decreases rapidly after 8.82 s. When fundamental period is 8.82 s, the spectrum value under FFH long-period ground movements reaches the peak of 1.093. And it is about 12.1 and 2.4 times of those under common and NFPL long-period ground movements.
Fig. 3Displacement response spectra
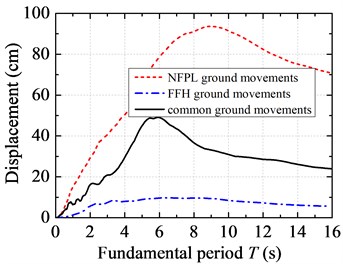
a) Seismic displacement spectra
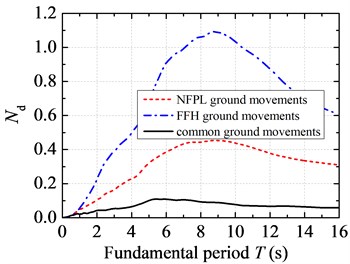
b) Normalized displacement spectra
4. Comparison of standard response spectra of long-period ground movements with code design spectrum
4.1. Standard response spectra of long-period ground movements
The acceleration response spectrum of actual earthquake records is smoothed and normalized to the form of code design spectrum, and this process is called the calibration of acceleration response spectrum. Currently, the least-square and minimization method for fitting and calibrating response spectrum is the most widely used in the seismic design of buildings. The standard deviation between the fitted response spectrum calibrated by the least-square and minimization method and the original response spectrum is the lowest. And the shape of the fitted spectrum is very similar to that of original spectrum. Therefore, the least-square and minimization method can be employed to calibrate the normalized acceleration spectra about two types of long-period ground movements.
Zhou et al., who employed the earthquake influence coefficient as the evaluation index of design spectra curves, evaluated the reliability of long-period segments of seismic design spectra [24]. The significant difference between this paper and the reference is that the dynamic magnification factor is used here for the standard response spectrum of long-period ground movements. Both of them present similar four-segment curves. According to the curve shape of the current code design spectrum usually applied in China [25], the calibrated standard response spectrum by the segmented least-square and minimization method is composed of four segments, which can be shortened as:
where, is the maximum value of dynamic magnification factor (i.e. platform segment height), and platform value is generally within 2-3; is the characteristic period (i.e. the period in the second inflection point), which can be determined by site condition, earthquake magnitude and epicentral distance. According to the influence of earthquake magnitude and epicentral distance, the design earthquake is divided into three groups in China's specification. So, the characteristic period can be determined by site classifications and design earthquake groups.
The least-square and minimization method is a mathematical optimization technique, and it finds the best function match of the data by minimizing the sum of squares of errors. The least-square and minimization method can be used to easily obtain the unknown data, and minimize the sum of squares of errors between the obtained data and the actual data. In this paper, by searching for the best two characteristic parameters (platform value and characteristic period), the sum of squares of errors between the fitted response spectrum and the actually normalized acceleration spectrum is minimized. Further, the calibrated standard response spectra under NFPL and FFH long-period ground movements as shown in Fig. 4 and Fig. 5 can be determined:
where, is the fitted spectrum; is the statistical average spectrum. and are automatically processed by minimizing . That is, the solution of Eq. (3) needs to be satisfied:
In this paper, the earthquake records in the C and D site classifications of NFPL long-period ground movements and C, D and E site classifications of FFH long-period ground movements are selected for the next study regardless of magnitude and distance. And the C, D and E site classifications in NEHRP correspond to the II, Ⅲ and IV site classifications in China’s code, respectively. The seismic design spectrum are extended to 10 s in the long-period segment according to the existed stretching trend of the current code. At the same time, the average normalized acceleration spectra of long-period ground motion records are drawn with corresponding fitted spectra in the same coordinate system.
4.1.1. Standard response spectra of NFPL long-period ground movements
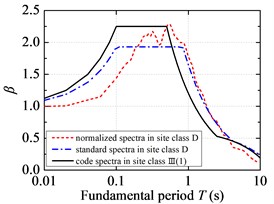
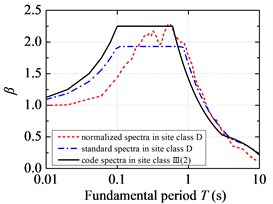
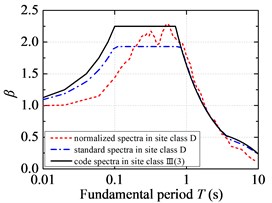
Fig. 4 illustrates the comparison of standard response spectra of NFPL long-period ground movements with the current code design spectra. On the whole, the code design spectrum overestimates the structural seismic response in the short period under NFPL long-period ground movements, while it underestimates the structural seismic response in the long period under NFPL long-period ground movements. However, the maximum value of structural fundamental period in the current code only reaches 6 s. It is suggested that the fundamental period of a SDOF system should be extended to consider the influence on long-period structures acted by a long-period earthquake. By comparing the standard response spectra in the C site classification of NFPL long-period ground movements with the seismic design spectra in the II site classification, the gaps between the fitted platform values of standard response spectra and those of code design spectra are very low, yet the fitted characteristic periods are greatly different from those of the current code. When the same are compared in the D site classification of NFPL long-period ground movements with the seismic design spectra in the Ⅲ site classification, the fitted platform values of standard response spectra are greatly different from those of code design spectra, yet the gaps between the fitted characteristic periods and those of the current code are very low. When the fundamental period of a SDOF system is beyond 0.8 s, the code design spectrum seriously underestimates the structural seismic response under NFPL long-period ground movements in the first design earthquake group, while it slightly underestimates the structural response under NFPL long-period ground movements in the third design earthquake group.
Fig. 4Standard response spectra of NFPL long-period ground movements and code design spectra: a) the first design earthquake group; b) the second design earthquake group; c) the third design earthquake group
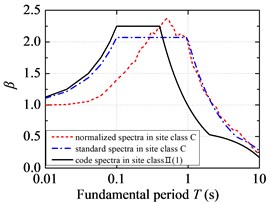
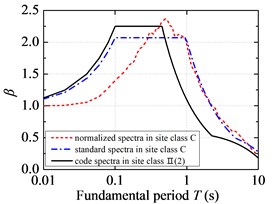
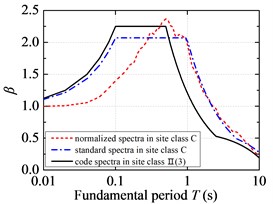
a)
b)
c)
4.1.2. Standard response spectra of FFH long-period ground movements
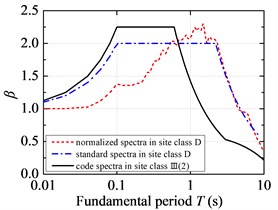
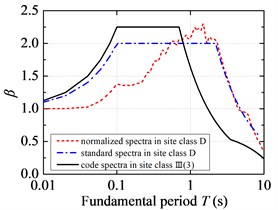
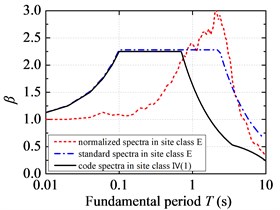
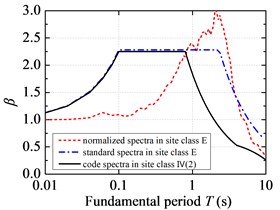
Fig. 5 demonstrates the comparison of standard response spectra of FFH long-period ground movements with the current code design spectra. The standard response spectra of FFH long-period ground movements are less than the current code design spectra in the short period. Considering the code design is based on a certain low probability of exceedance, so it is reasonable to design short-period structures by adopting the current code for seismic design of buildings. However, the standard response spectra of FFH long-period ground movements are larger than the current code design spectrum in the medium-long and long period, and the corresponding probability of exceedance is relatively high from the probability point of view. So it is unsafe to design structures with medium-long and long fundamental period if the current code for seismic design of buildings is adopted. For FFH long-period ground movements with long-distance propagation, it contains more long-period components due to the filtering effect of low-frequency amplification and high-frequency attenuation. The period corresponding to the inflection point in the peak region of standard response spectra is shifted to the long-period direction, and it is suggested that the long-period part of standard response spectra should not be segmented and the attenuation index should be always taken as 0.9. The fitted characteristic periods of standard response spectra under FFH long-period ground movements are much larger than that of the current code design spectrum. The fitted platform values of standard response spectra in the C and D site classifications are around 2.05, which is lower than that of the current code design spectrum. However, the fitted platform values in the E site classification of FFH long-period ground movements are slightly higher than specification due to the soft-soil filtering effect.
Fig. 5Standard response spectra of FFH long-period ground movements and code design spectra: a) the first design earthquake group; b) the second design earthquake group; c) the third design earthquake group
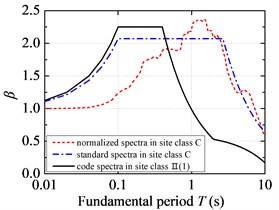
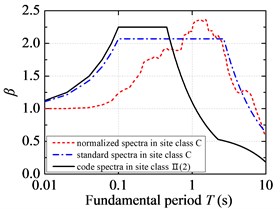
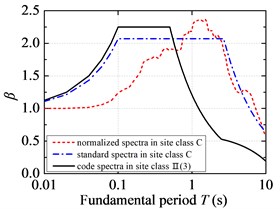
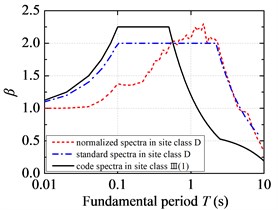
a)
b)
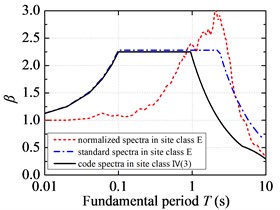
c)
4.2. Comparison on characteristic parameters of response spectra
The platform value and characteristic period are two important characteristic parameters of seismic design spectrum. The platform value can reflect the amplitude intensity of earthquake action, while the characteristic period can reflect the spectrum characteristic of earthquake action. The platform value is related to a variety of factors, and the site condition is one of the most important factors.
Table 4Characteristic parameters of standard response spectra
Characteristic parameters | Site class (NFPL ground movements) | Site class (FFH ground movements) | |||
C | D | C | D | E | |
Platform value | 2.07 | 1.93 | 2.07 | 2.00 | 2.28 |
Characteristic period | 0.98 | 0.84 | 2.68 | 2.21 | 2.31 |
Table 5Characteristic parameters of code design spectra
Characteristic parameters | Site class (first design earthquake group) | Site class (second design earthquake group) | Site class (third design earthquake group) | ||||||
II | Ⅲ | IV | II | Ⅲ | IV | II | Ⅲ | IV | |
Platform value | 2.25 | 2.25 | 2.25 | 2.25 | 2.25 | 2.25 | 2.25 | 2.25 | 2.25 |
Characteristic period | 0.40 | 0.50 | 0.70 | 0.45 | 0.60 | 0.80 | 0.50 | 0.70 | 0.95 |
Table 4 illustrates the characteristic parameters of platform value and characteristic period about the standard response spectra in various site classifications under long-period ground movements. Table 5 illustrates the characteristic parameters of platform value and characteristic period about the code design spectra in various site classifications and design earthquake groups.
4.2.1. Platform value
The fitted platform values of standard response spectra under NFPL and FFH long-period ground movements both are lower than 2.25 of the current code design spectrum. And the fitted platform values under NFPL long-period ground movements are about 2.0, and reach 89 % of the current code design spectrum, while the fitted platform values under FFH long-period ground movements are slightly higher than those under NFPL long-period ground movements. Even the fitted platform value in the E site classification of FFH long-period ground movements exceeds the specified value in the current code. Therefore, the platform value of standard response spectra under long-period ground movements, especially FFH long-period ground movements, should be increased appropriately to improve the safety reserve.
4.2.2. Characteristic period
The fitted characteristic periods of standard response spectra under NFPL and FFH long-period ground movements both exceed those of the current code design spectra. The fitted characteristic period in the C site classification of NFPL long-period ground movements is about 2 times of the current code design spectrum, while the fitted characteristic period in the C site classification of FFH long-period ground movements reaches 5 times of the specified value in the current code. Therefore, the characteristic period of standard response spectra under long-period ground movements (especially for FFH long-period ground movements) should be appropriately amplified.
4.2.3. Site classification
For NFPL and FFH long-period ground movements, the fitted platform values and characteristic periods of standard response spectra in the D site classification are less than those in the C site classification. The site condition has little influence on the standard response spectra under NFPL long-period ground movements, yet the fitted platform value in the E site classification of FFH long-period ground movements is slightly higher than the specified value in the current code due to the filtering effect. Therefore, the influence on response spectra under soft-soil site of FFH long-period ground movements should mainly be considered in the corrections of platform value and characteristic period.
4.2.4. Design earthquake group
The design earthquake is divided into three types of groups in the current code, and the platform value 2.25 of code design spectrum in three groups of design earthquake basically satisfies the height requirement of platform value for standard response spectra under long-period ground movements. The characteristic periods of the current code design spectra in the first design earthquake group are biased to the short-period direction, while those in the third design earthquake group are biased to the long-period direction. Therefore, the curve shape of code design spectrum in the third design earthquake group is more consistent with the form of standard response spectra under long-period ground movements.
4.2.5. Limitation
Table 4 indicates the fitted platform values and characteristic periods of standard response spectra in the D site classification are less than those in the C site classification under two types of long-period ground movements. The main reasons are as follows: On the one hand, the long-period ground motion records are selected according to the distribution pattern of Fourier amplitude spectrum. They all have a uniform spectrum distribution, which leads to the inhomogeneous variation of characteristic parameters with the change of site classifications. On the other hand, the selected number of long-period ground motion records is limited, and the variation coefficient of statistical characteristic parameters is very large. So a large discrepancy of characteristic parameters with the variation of soil-shear wave velocity is accompanied, which is not enough to clarify its variation rule of response spectra with the change of site classification.
5. Conclusions
Firstly, two types of special long-period and common earthquake records are selected for this research. Then, the fundamental period of a SDOF system is extended to 16 s with the damping ratio of 5 %, and the response spectrum characteristics of long-period ground movements are analyzed. Lastly, the calibrated standard response spectra of long-period ground movements are compared with the code design spectra. The main conclusions are obtained as follows:
1) The seismic response spectra of NFPL long-period ground movements are higher than those under common and FFH long-period ground movements. The peaks of the normalized acceleration spectra under three types of earthquake action are close to each other, but the structural fundamental periods corresponding to the spectrum peaks present significant differences. Moreover, the normalized acceleration spectra under NFPL and FFH long-period ground movements are relatively dispersed throughout the fundamental period, and they are not concentrated in the period range of 1 s as that under common ground movements.
2) Code design spectrum overestimates the structural seismic response in the short period under NFPL and FFH long-period ground movements, while it underestimates the structural seismic response in the long period. It is suggested that the long-period segment of standard response spectrum under FFH long-period ground movements should not be segmented and the attenuation index should be always taken as 0.9. The fitted platform values of NFPL and FFH long-period ground movements are lower than 2.25 in the code design spectrum, while the fitted characteristic periods of NFPL and FFH long-period ground movements both exceed that of code design spectrum.
3) The site condition has little influence on the standard response spectrum of NFPL long-period ground movements, yet the fitted platform value in the E site classification of FFH long-period ground movements is slightly larger than the specified value in the current code due to the soft-soil filtering effect. The curve shape of code design spectrum in the third design earthquake group is more consistent with the form of seismic design spectrum under long-period ground movements.
4) Dynamic magnification factor is used in this study for the standard response spectrum of long-period ground movements. The fundamental period of a SDOF system of China’s current code design spectrum should be extended to consider the influence on long-period structures acted by a long-period earthquake. Further, it accounts for the resonance effect of long-period ground movements which ensures the seismic design safety of long-period structures.
5) The selected earthquake records are considered for a limited number of earthquake events in this paper, and the reliability and rationality of obtained conclusions remain to be further studied and verified. But it can lay the foundation and provide a reference for seismic response analysis of engineering structures and value revision as per the valid codes for seismic design of buildings. It is particularly noted that the value revision of long-period segment about the design response spectrum is made for creating the corresponding codes in China, yet the similar method of theoretical analysis is applicable to the same processes in other countries too.
References
-
Yang D. X., Pan J. W., Li G. Non-structure-specific intensity measure parameters and characteristic period of near-fault ground motions. Earthquake Engineering and Structural Dynamics, Vol. 38, Issue 11, 2009, p. 1257-1280.
-
Li C. F., Zhang Y., Zhao J. B., Tang H. Long-period ground motion characteristic of the 1999 Jiji (Chi-Chi), Taiwan, mainshock and aftershocks. Acta Seismologica Sinica, Vol. 19, Issue 4, 2006, p. 448-460.
-
Yang W. L., Zhu S. C., Hong H. C., Tao X. S., Tang, Z. L. Characteristics of far-field ground motion of Wenchuan earthquake and the effect on long-periodic structures. Journal of Disaster Prevention and Mitigation Engineering, Vol. 29, Issue 4, 2009, p. 473-478, (in Chinese).
-
Takewaki I., Fujita K., Yoshitomi S. Uncertainties in long-period ground motion and its impact on building structural design: case study of the 2011 Tohoku (Japan) earthquake. Engineering Structures, Vol. 49, 2013, p. 119-134.
-
Furumura T. Destructive near-fault strong ground motion from the 2016 Kumamoto prefecture, Japan, M7.3 earthquake. Landslides, Vol. 13, Issue 6, 2016, p. 1519-1524.
-
Xu L. J., Hu J. J., Xie, L. L. On characteristics of ground motion parameters for special long-period ground motion. Journal of Earthquake Engineering and Engineering Vibration, Vol. 28, Issue 6, 2008, p. 20-27, (in Chinese).
-
Ucak A., Mavroeidis G. P., Tsopelas P. Behavior of a seismically isolated bridge crossing a fault rupture zone. Soil Dynamics and Earthquake Engineering, Vol. 57, 2014, p. 164-178.
-
Zhang S. R., Wang G. H. Effects of near-fault and far-fault ground motions on nonlinear dynamic response and seismic damage of concrete gravity dams. Soil Dynamics and Earthquake Engineering, Vol. 53, 2013, p. 217-229.
-
Takewaki I., Murakami S., Fujita K., Yoshitomi S., Tsuji M. The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dynamics and Earthquake Engineering, Vol. 31, Issue 11, 2011, p. 1511-1528.
-
Cheng Y., Bai G. L., Jiang L. J. Response analysis of high-rise frame structure in the far-field long-period ground motions. World Earthquake Engineering, Vol. 32, Issue 3, 2016, p. 145-152, (in Chinese).
-
Dong Y. R., Cheng Y., Bai G. L. Analysis of spectrum characteristics and intensity indices for near-fault ground motions. Industrial Construction, Vol. 45, Issue 7, 2009, p. 102-107, (in Chinese).
-
Cheng Y., Bai G. L., Dong Y. R. Spectrum characterization of two types of long-period ground motions and seismic behavior of frame-core wall structures under multidimensional earthquake records. The Structural Design of Tall and Special Buildings, Vol. 27, Issue 16, 2018, p. e1539.
-
Dong Y. R., Xu Z. D., Li Q. Q., Xu Y. S., Chen Z. H. Seismic behavior and damage evolution for retrofitted RC frames using haunch viscoelastic damping braces. Engineering Structures, Vol. 199, 2019, p. 109583.
-
Chung Y. L., Nagae T., Hitaka T., Nakashima M. Seismic resistance capacity of high-rise buildings subjected to long-period ground motions: E-Defense shaking table test. Journal of Structural Engineering, Vol. 136, Issue 6, 2010, p. 637-644.
-
Ariga T., Kanno Y., Takewaki I. Resonant behaviour of base-isolated high-rise buildings under long-period ground motions. The Structural Design of Tall and Special Buildings, Vol. 15, Issue 3, 2006, p. 325-338.
-
Chen Q. J., Yuan W. Z., Li Y. C., Cao L. Y. Dynamic response characteristics of super high-rise buildings subjected to long-period ground motions. Journal of Central South University, Vol. 20, Issue 5, 2013, p. 1341-1353.
-
Ma N., Xu L. J., Xie L. L. Study on the period parameters of ground motions during the Chi-Chi earthquake. Journal of Earthquake Engineering and Engineering Vibration, Vol. 28, Issue 1, 2008, p. 11-16, (in Chinese).
-
Xu L. J., Xie L. L. Characteristics of frequency content of near-fault ground motions during the Chi-Chi earthquake. Acta Seismologica Sinica, Vol. 18, Issue 6, 2005, p. 707-716.
-
Geng S. W., Tao X. X., Wang G. X. Study on the provisions for the values of design response spectrum in long period section. World Earthquake Engineering, Vol. 24, Issue 2, 2008, p. 111-116, (in Chinese).
-
Zhou Y. N., Zhou Z. H., Yu H. Y. A study on long period portion of design spectrum. Journal of Earthquake Engineering and Engineering Vibration, Vol. 24, Issue 2, 2004, p. 11-16, (in Chinese).
-
Tso W. K., Zhu T. J., Heidebrecht A. C. Engineering implication of ground motion A/V ratio. Soil Dynamics and Earthquake Engineering, Vol. 11, Issue 3, 1992, p. 133-144.
-
Fajfar P., Vidic T. Consistent inelastic design spectrum: hysteretic and input energy. Earthquake Engineering and Structural Dynamics, Vol. 23, Issue 5, 1994, p. 523-537.
-
Loh C. H., Wan S., Liao W. I. Effects of hysteretic model on seismic demands: consideration of near-fault ground motions. The Structural Design of Tall and Special Buildings, Vol. 11, Issue 3, 2002, p. 155-169.
-
Zhou J., Fang X. D., Jiang Y. Comparison of the earthquake response of super-high-rise building structures based on different seismic design spectrum. Journal of Engineering Research, Vol. 7, Issue 4, 2019, p. 58-80.
-
Code for seismic design of buildings (GB50010-2010). China Construction Industry Press, 2010, (in Chinese).
About this article
The present work was supported by the National Natural Science Foundation of China (No. 52074112), Provincial Education Department Program of Hubei Province (No. D20182601) and Doctoral Research Foundation of Hubei University of Arts and Science (No. 2059070). These supports were greatly appreciated.
