Abstract
Euler-Bernoulli beam model is used to analyze the thermal vibration of cracked metallic and laminated composite beam with fully clamped ends. An analytical solution technique is proposed to investigate the natural vibration of cracked beam subjected to axial thermal load. An open and stable crack is considered perpendicular to the beam axis. In this study, three different types of material such as steel, copper and aluminum and their composition are used to analyze the thermal effect on different modes of frequency. The effects of thermal stress on the vibration of cracked metallic and composite fully clamped beam are revealed. The results show that the effect of temperature is significant on the natural frequency of cracked metallic and composite beam.
Highlights
- The effect of thermal vibration depends on length to height ratio of the beam
- The effect of temperature is more significant in first mode of frequency
- Under thermal load composite beam is very effective than metallic beam
1. Introduction
Effect of temperature is one of the important features for designing of structures efficiently. Unfortunately, thermal effect is ignored in most of the research which leads to incorrect results. A small change in temperature may cause a large variation in the behavior of beam vibration [1]. Thermal stresses are considered as mechanical stresses of the elements. It is the result of contraction or expansion of structural elements due to the applied thermal load. When an element is subjected to the rise of temperature it expands and when it loses temperature, it contracts. The expansion and contraction of the element due to the temperature is proportional to the change of temperature. This proportionality depends on the coefficient of linear thermal expansion of the material [2]. According to the theory of linear thermo-elasticity, the thermal strain is linearly added with the mechanical strain. That is why the equations of equilibrium and compatibility of thermal problems are the same as the elasticity problem. According to this assumption, many techniques that have been used to solve the elasticity problems are applicable to the thermo-elasticity problem as well [3].
Interest in multifunctional composite materials has increased rapidly in recent years. Laminated composite materials are also a very efficient type of composition. Laminated composite materials are formed by different layers of two or more materials that are effectively bonded together. It is a combination of a large number of fibers in a thin layer of matrix. Fibers in the lamina may be continuous or discontinuous, arranged in a specific direction or in a random orientation [4]. Lamination is a very useful technique to achieve more efficient material. Lamination can emphasize the properties of material such as strength, stiffness, low weight, corrosion resistance, thermal insulation, etc. [5-7].
The effect of thermal vibration on the cracked composite beam is very rare in the open literature. Therefore, thermal effects on macro mechanics also achieve substantial attention among researchers. Zhang et al. [8] studied the thermal effects on high-frequency vibration of beams. Their results showed that the spatial distributions and levels of energy density can be affected by the thermal effects. Cui and Hu [9] examined thermal buckling and natural vibration of the beam with an axial stick-slip-stop boundary. Lia and Zhang [10] investigated the thermal effect on vibration and buckling analysis of thin plates with cracks. Their results revealed that the dynamic behavior of structural elements is significantly affected by thermal effects.
In this paper, the effects of temperature on the dynamic behavior of cracked metallic and composite beam are investigated. Our main concern is to compare the effectiveness of a fully clamped metallic and composite beam under crack and temperature. The governing differential equations with boundary and intermediate conditions are solved using analytical techniques. The effects of crack severity, crack position and beam length to height ratio on the frequencies of the heated beam are investigated. On the other hand, the effect of temperature on the vibration of the cracked composite beam is analyzed and compared with the metallic beam in detail.
2. Settings of the problem
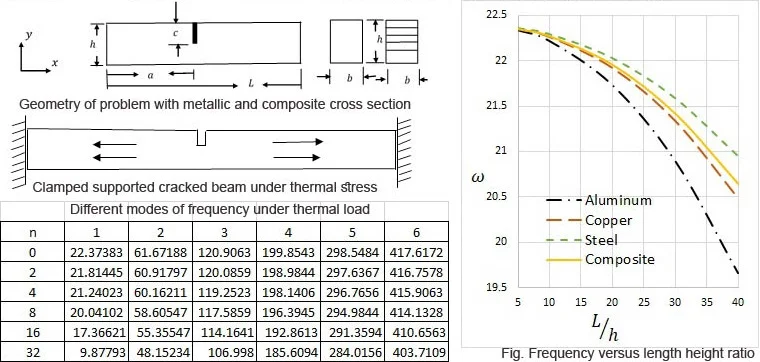
A diagram of a cracked beam is illustrated in Fig. 1. The cross section of the beam is rectangular. is the length and is the width of the beam respectively. Beam is isotropic and homogeneous where is the density of the metallic beam. Single crack is placed at the location of of the beam. The crack is considered as stable crack whose depth is and is the ratio of crack height and beam height. Three different types of material (Aluminium, Copper, and Steel) are considered for the metallic beam as shown in Table 1.
A composite laminated material is also considered for the beam which is formed by three different materials such as aluminum, copper, and steel in a certain combination.
Fig. 1Geometry of the problem
Table 1Material properties
Material | Young’s modulus (GPa) | Coefficient of thermal expansion (°C) | Density (kg/m3) |
Aluminium | 69 | 24x10-6 | 2780 |
Copper | 117 | 17x10-6 | 8960 |
Steel | 200 | 13x10-6 | 8050 |
3. Mathematical formulation
A beam is considered along the axis where transverse deflection is described along the axis. According to the theory of Euler-Bernoulli for small deflection, the equation of motion expressed by the transverse deflection can be obtained as:
For separating the variable, this function can be used. Then the Eq. (1) becomes:
Let us assume that the beam is homogenous having same temperature over its entire length. As a result of thermal expansion, an additional axial force can be presented as:
is the linear thermal extension coefficient, is the temperature difference between the actual and initial temperature. Let us introduce dimensionless variables:
The Eq. (2) becomes:
Using this function , we can write the characteristic equation as follow:
Roots of the equation can be presented as follow:
Solutions of the equation are:
Boundary conditions for the fully clamped beam as follow:
These four boundary conditions and other four intermediate conditions for crack are used to solve the Eqs. (6) and (7). For crack, the stress intensity factor for the single edge notched tension is presented as follow (see [11]):
Using the intensity factor intermediate conditions for the crack can be defined as below:
In composite beam, the Young’s modulus of composite system can be written as:
Thermal expansion coefficient of composite material can be presented as:
4. Results and discussion
The temperature effect on the vibration of metallic and composite beams is significant. To develop a reliable model to analyse thermal effect on metallic and composite beam are also very essential. In this section, the outcomes of this analysis are presented with graphs and tables. Three different materials such as steel, copper, aluminium and their composite are used in this analysis. In composite, these three materials such as steel, copper, and aluminium are used as a ratio of 40 %, 30 %, and 30 % respectively. The results of this analysis show good accordance with the papers of other researcher in open literature.
Table 2Natural frequency of solid beam with clamped ends
1 | Frequency in different modes | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
Current work | 22.095 | 61.295 | 120.49 | 199.44 | 298.09 | 417.19 |
Jiang and Wang [12] | 21.736 | 57.967 | 107.74 | 166.61 | 231.10 | 298.71 |
Table 2 illustrates the dimensionless natural frequency of fully clamped solid beam. Current research data show good agreement with data of other researcher [12] in lower mode of frequency. In current work, Euler-Bernoulli theory is used. On the other hand, Jiang and Wang [12] used nonlocal theory of elasticity with nonlocal parameter value 0.05. That is why, there are some differences in both data sets in higher modes of frequency.
Table 3Natural frequency of solid beam for different axial loads
Frequency in different modes | ||||||
1 | 2 | 3 | 4 | 5 | 6 | |
0 | 22.37383 | 61.67188 | 120.9063 | 199.8543 | 298.5484 | 417.6172 |
2 | 21.81445 | 60.91797 | 120.0859 | 198.9844 | 297.6367 | 416.7578 |
4 | 21.24023 | 60.16211 | 119.2523 | 198.1406 | 296.7656 | 415.9063 |
8 | 20.04102 | 58.60547 | 117.5859 | 196.3945 | 294.9844 | 414.1328 |
16 | 17.36621 | 55.35547 | 114.1641 | 192.8613 | 291.3594 | 410.6563 |
32 | 9.87793 | 48.15234 | 106.998 | 185.6094 | 284.0156 | 403.7109 |
Table 3 depicts the natural frequency of solid beam under dimensionless axial loads. Natural frequency decreases with increase of axial load. Axial load is very effective on the 1st mode of frequency instead of higher mode of frequency.
Table 4Natural frequency of composite beam for different temperatures
=20 | Aluminum (30%), Copper (30%), Steel (40%) | Aluminum (40%), Copper (30%), Steel (30%) | Aluminum (30%), Copper (40%), Steel (30%) | ||||||
1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
0 | 22.3730 | 61.6738 | 120.898 | 22.3744 | 61.6736 | 120.898 | 22.373 | 61.6738 | 120.898 |
5 | 22.2676 | 61.5352 | 120.742 | 22.2637 | 61.5273 | 120.742 | 22.2676 | 61.5273 | 120.742 |
10 | 22.1660 | 61.3867 | 120.602 | 22.1543 | 61.377 | 120.572 | 22.1582 | 61.3789 | 120.586 |
20 | 21.9551 | 61.1055 | 120.289 | 21.929 | 61.0723 | 120.246 | 21.9395 | 61.0898 | 120.258 |
30 | 21.7402 | 60.8242 | 119.977 | 21.7046 | 60.7695 | 119.914 | 21.7207 | 60.793 | 119.945 |
40 | 21.5254 | 60.5352 | 119.668 | 21.4746 | 60.4727 | 119.586 | 21.498 | 60.4961 | 119.617 |
50 | 21.3076 | 60.2461 | 119.345 | 21.2441 | 60.1602 | 119.254 | 21.2715 | 60.1992 | 119.305 |
Table 4 reveals the effect of temperature on natural frequency of composite beam. Three different types of materials such as steel, copper and aluminum are used in these composites. Three different composition ratios of these materials are used to create three different composites. Table data show that increase of temperature decreases frequency. On the other hand, ratio of these compositions is not very significant on natural frequency.
Fig. 2Frequency versus change of temperature and length to height ratio
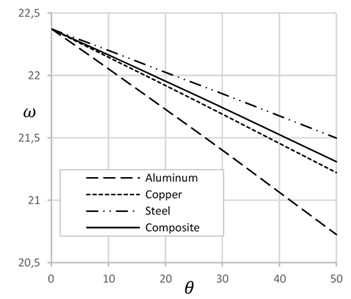
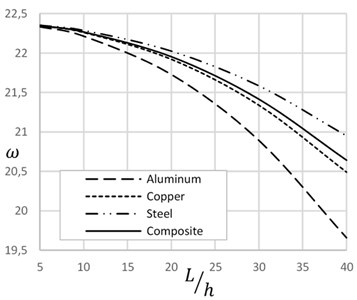
Fig. 2 illustrates the effect of temperature and length to height ratio on the natural frequency of beam for different materials. Natural frequency decreases with increase of temperature and the length to height ratio. Temperature increases axial tension that decreases natural frequency. Similarly, increase of length to height ratio decreases height and cross sectional area of beam that increases axial stress. Increase of axial stress decreases natural frequency. Composite material shows the effective results considering the behavior of other materials.
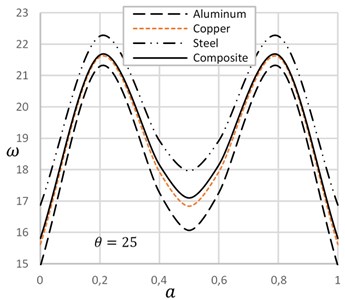
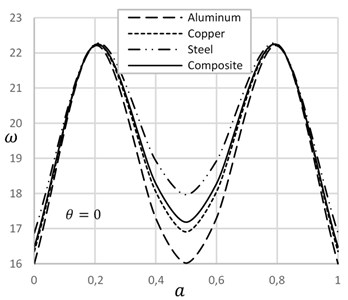
Fig. 3 displays the effect of crack depth ratio on the natural frequency presence and absence of temperature. This figure depicts that increase of crack depth ratio decreases natural frequency. On the absence of temperature, the effect of crack depth ratio is more significant than the presence of that. High temperature expands the length of the beam and reduces the width of the crack that decreases slightly the effect of crack on frequency.
Fig. 4 demonstrates the effect of temperature on the frequency of cracked beams with different crack-depth ratio. At the low crack depth ratio, frequency decreases with the increase of temperature. On the other hand, at the high crack depth ratio, frequency increases with the increase of temperature. Increase of temperature expands the length of the beam and decreases the width of the crack that enhances the frequency of the beam. Fig. 5 describes the effect of crack location on the natural frequency of beam on presence and absence of temperature. Crack position at the ends and at the mid of the beam show lower frequency. On the other hand, in between crack position shows higher frequency of the beam. Frequency of crack beam with temperature is more significant than the crack without temperature.
Fig. 3Frequency versus crack depth ratio with and without temperature
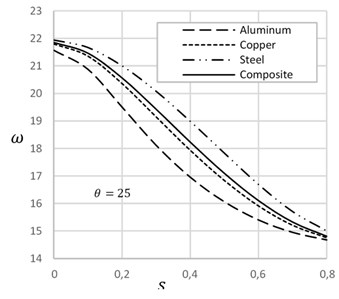
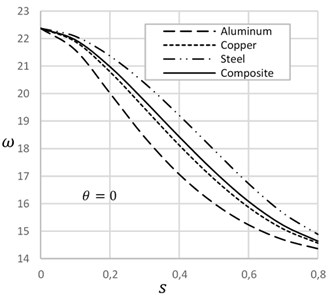
Fig. 4Frequency versus change of temperature for different crack depth ratios
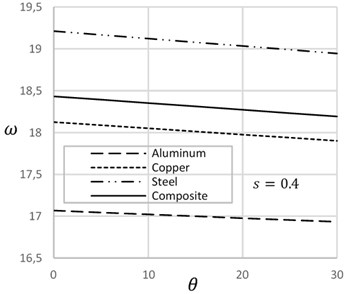
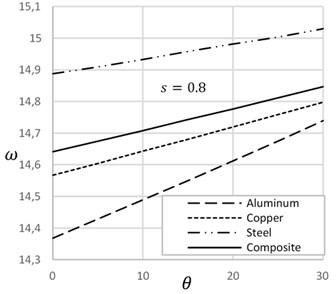
Fig. 5Frequency versus crack location with and without temperature
5. Conclusions
In this study, Euler-Bernoulli beam theory is employed to develop an analytical technique for analyzing thermal effect on dynamic behavior of cracked metallic and composite beam. The results are presented for three different types of material and their composite. The results of this investigation showed that the effect of thermal vibration depends on length to height ratio of the beam. The effect of temperature is more significant in first mode of frequency. In higher mode of frequency, the temperature effect is less significant. Under thermal load composite beam is very effective than metallic beam.
References
-
Avsec J., Oblak M. Thermal vibrational analysis for simply supported beam and clamped beam. Journal of Sound and Vibration, Vol. 308, 2007, p. 514-525.
-
Barron R. F., Barron B. R. Design for Thermal Stresses. John Wiley and Sons, 2012.
-
Hetnarski R. B., Eslami M. R. Thermal Stresses-Advanced Theory and Applications. Springer Science+Business Media, 2009.
-
Mukhopadhyay M. Composite Materials and Structures. Universities Press (India) Private Limited, 2004.
-
Robert M. J. Mechanics of Composite Materials. Taylor and Francis, 1999.
-
Vasiliev V. V. Advanced Mechanics of Composite Materials and Structural Elements. Elsevier, 2013.
-
Gibson R. F. Principles of Composite Material Mechanics. CRC Press, Taylor and Francis Group, 2012.
-
Zhang W., Chen H., Zhu D., Kong X. The thermal effects on high-frequency vibration of beams using energy flow analysis. Journal of Sound and Vibration, Vol. 333, 2014, p. 2588-2600.
-
Cui D. F., Hu H. Y. Thermal buckling and natural vibration of the beam with an axial stick-slip-stop boundary. Journal of Sound and Vibration, Vol. 333, 2014, p. 2271-2282.
-
Lai S. K., Zhang L. H. Thermal effect on vibration and buckling analysis of thin isotropic/orthotropic rectangular plates with crack defects. Engineering Structures, Vol. 177, 2018, p. 444-458.
-
Anderson T. L. Fracture Mechanics Fundamentals and Applications. CRC Press, Taylor and Francis Group, 2017.
-
Jiang J., Wang L. Analytical solutions for thermal vibration of nanobeams with elastic boundary conditions. Acta Mechanica Solida Sinica, Vol. 30, 2017, p. 474-483.
About this article
The partial support from Estonian Doctoral School of Mathematics and Statistics is acknowledged.
