Abstract
Cell dynamics is one of the most investigated areas under the field of biomechanics. Scaling plays a crucial role in determining the dynamic characteristics of biological systems. In the present investigation, cuboidal and cylindrical models of different scales are analysed to depict the dependence of natural frequency on the scaling factors. Three approaches, namely lumped mass system, finite element model (FEM) and numerical approach using Ansys are used to determine the fundamental natural frequencies. Different scaling factors, namely nano, micro (original size), millimeter and meter are considered for the analysis. The results indicate that the natural frequency varies inversely with the size of the cell by the same factor. A simple mathematical relation is derived to support this claim. Results are illustrated with numerical examples and corresponding mode shapes are reported.
1. Introduction
All living organisms are complex constructions of fundamental units called cells. Cell dynamics govern the basic functionality of the cells. Many researchers have made an attempt to study and understand dynamics of cells largely through experimentation and simulation. Experimentation reveals many mechanical characteristics of the cell like Young's modulus, density, surface stiffness etc. These characteristics can be used to develop a mathematical model to represent dynamic characteristics of the cell. In spite of the studies carried out in establishing basic dynamic characteristics of the cell, limited number of studies are carried out regarding the effect of scaling on the dynamics of the cell.
Wang et al., [1] modeled the bone forming cell as a continuum finite element model for ten different shapes and obtained their respective natural frequencies and there is some ambiguity in the results obtained. Uzer et al., [2] presented a finite element model of an adherent cell subjected to both acceleration and fluid shear using Abaqus to analyze the cell deformations. Fabry et al., [3] presented a study which considered the cytoskeletal polymers as a glassy material and investigated the variation of mechanical properties for a variety of cells with different scale factors. Wee and Voloshin [4] investigated the vibrations of a cell using both a continuum model and a tensegrity model. The frequencies range of the cell are observed in order of 20-60 Hz. Zarandi et al., [5] classified natural frequencies of cells of differing mechanical characteristics and shapes. The reported frequencies are in the range of 140-510 kHz.
This paper mainly focuses on the role of scaling factor for dynamic analysis of cells. An effort is made to model the cells using both analytical and numerical approaches. It is observed that there are noticeable differences in natural frequenciesobtained using the two mentioned methods. Study reveals that the natural frequencies obtained for nm size model to m size model always have a definite multiplication factor relation. This is also proved through our simple illustrative calculation.
2. Modelling and simulation
The exact shape of a cell is very hard to generalize. Most reported literature on study of cells have considered cell shapes as either cuboidal, spherical, cylindrical, hemispherical etc., for the sake of simplicity [6]. For the present investigation simple, possible and widely acceptable shapes like cuboidal and cylindrical model are used as shown in Fig. 1.
Fig. 1Cuboidal and cylindrical model of cell
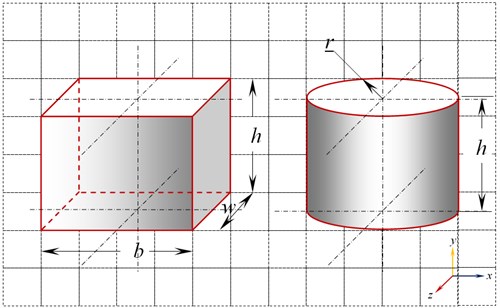
Scaling factors of 10-3, 103 and 106 are used to scale the initial micro size cell model of both cuboidal and cylindrical shapes. The dimensions of the cuboidal and cylindrical models are given in Table 1.
Table 1Dimensions of cuboidal and cylindrical model
Cuboidal model | Cylindrical model | |||||
Model | Breadth, (mm) | Width, (mm) | Height, (mm) | Model | Radius, (mm) | Height, (mm) |
Cb1 | 20×10-6 | 20×10-6 | 15×10-6 | Cy1 | 10×10-6 | 15×10-6 |
Cb2 | 20×10-3 | 20×10-3 | 15×10-3 | Cy2 | 10×10-3 | 15×10-3 |
Cb3 | 20 | 20 | 15 | Cy3 | 10 | 15 |
Cb4 | 20×103 | 20×103 | 15×103 | Cy4 | 10×103 | 15×103 |
Membrane and nucleus play a negligible role in determining the stiffness of the cell [7]. For both the cuboidal and cylindrical models, the material properties of cytoplasm are utilized and are tabulated in Table 2.
Table 2Material properties of cytoplasm
Young’s modulus (Pa) | Poisson’s ratio | Density (kg/m3) |
1,500 | 0.37 | 1,500 |
Three approaches are adopted to demonstrate the effect of scaling on the dynamic characteristics of cell. Firstly, lumped mass approach, one of the fundamental approaches for dynamic analysis is utilized. Both cuboidal and cylindrical cell models are evaluated as a lumped mass system and their respective equivalent mass and stiffness relations are shown in Fig. 2.
Fig. 2Lumped mass system along with meq. and keq. relations
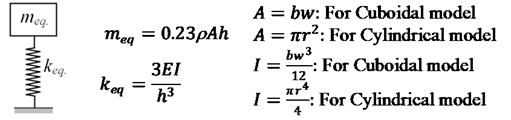
The fundamental natural frequency is evaluated using the relation:
Secondly, a finite element approach is used assuming the models as a cantilever beam. A beam element with two degree-of-freedom at each node is considered. Stiffness and mass matrix of the beam element is obtained from a reference paper by Chandrashekara et al. [8]. Ten elements are assumed along the height of the models to obtain the natural frequencies.
Finally, a numerical approach is used to carry out the modal analysis using Ansys (Workbench 18.1). Initially all the models are developed in SolidWorks2018 and exported to Ansys for analysis. Boundary condition is established by fixing the base surface. Proximity and curvature size function is used for meshing the models. The fundamental natural frequencies of both the models with four scaling factors using three different approaches are listed in Table 3.
Table 3First natural frequencies of cuboidal model in Hz
Cuboidal model | Cylindrical model | ||||||
Model | Lumped mass approach | FEM approach | Numerical (Ansys) | Model | Lumped mass approach | FEM approach | Numerical (Ansys) |
Cb1 | 1,47,49,377.65 | 1,43,59,129.42 | 78,92,800 | Cy1 | 1,27,73,335.73 | 1,24,35,370.86 | 75,71,500 |
Cb2 | 14,749.38 | 14,359.13 | 7,892.8 | Cy2 | 12,773.34 | 12,435.37 | 7,566.6 |
Cb3 | 14.749 | 14.359 | 7.8928 | Cy3 | 12.773 | 12.435 | 7.5666 |
Cb4 | 0.014749 | 0.014359 | 0.0078928 | Cy4 | 0.012773 | 0.012435 | 0.0075671 |
The results strongly indicate that scaling plays a crucial role during dynamic analysis of cells. As the overall size of the model is increased by a thousand times, the natural frequency is decreased by a thousand times. For lumped mass and finite element approaches, making appropriate substitution of parameters and simplifying, the relation for fundamental natural frequency is reduced to:
where, is a constant.
Eq. (2) has a good agreement with the scaling factor.
Even though the trend in results using scaling factors is followed for all three approaches, results obtained by numerical approach are not in good agreement with that of the lumped mass and FEM approaches. One of the reasons for this trend is due to non-slender nature of the models considered for modal analysis using numerical approach. Under cuboidal model investigation it is noticed that results obtained by numerical approach are approximately 0.54 to 0.55 times the results obtained by the other two approaches. Similarly, in the case of cylindrical model it is around 0.60 to 0.61.
For the meter scale model, mode shapes are obtained for both cuboidal and cylindrical models and are illustrated in Fig. 3 and Fig. 4 respectively.
To demonstrate the slender effect on the natural frequency in Ansys, the same cuboidal and cylindrical cross sections (millimeter model, i.e., Cb3 and Cy3 model) are modeled with a height of 140 mm (7 times the base size). The fundamental natural frequencies for both models are extracted using all the three approaches and are listed in Table 4.
It is noticed that the value of natural frequency obtained by lumped-mass and FEM approaches are very much in agreement with the results obtained by Ansys. First mode shape of the slender cuboidal and cylindrical model is shown in Fig. 5.
Fig. 3Mode shapes of cuboidal model
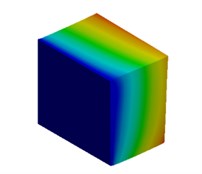
a) Nanometer model: Cb1
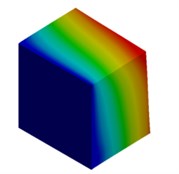
b) Micron model: Cb2
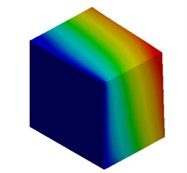
c) Millimeter model: Cb3
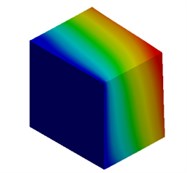
d) Meter model: Cb4
Fig. 4Mode shapes of cylindrical model
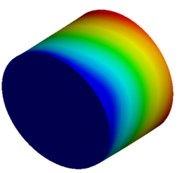
a) Nanometer model: Cy1
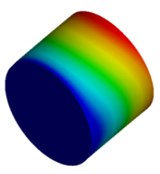
b) Micron model: Cy2
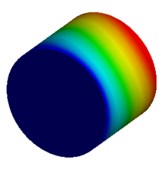
c) Millimeter model: Cy3
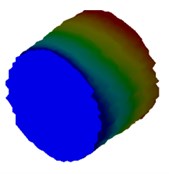
d) Meter model: Cy4
Table 4Natural frequencies of slender models
Cuboidal model | Cylindrical model | ||||||
Model | Lumped mass approach | FEM approach | Numerical (Ansys) | Model | Lumped mass approach | FEM approach | Numerical (Ansys) |
Cb3 | 0.16932 | 0.16484 | 0.16416 | Cy3 | 0.14663 | 0.14275 | 0.14256 |
It suggests that modeling and dynamic analysis of cells with different scales certainly affects the values of natural frequencies obtained. While analysing the bulky model, care should be taken to compare the values obtained by numerical approach with that of the traditional approaches.
Fig. 5Mode shapes and natural frequencies of slender model of cuboidal and cylinder model
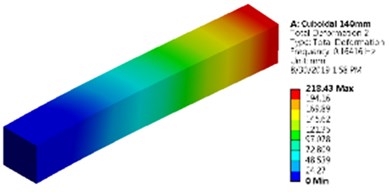
a) Cuboidal model as a slender model
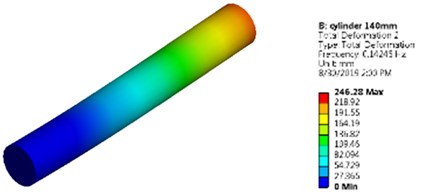
b) Cylindrical model as a slender model
3. Conclusions
The present investigation demonstrates the severity of scaling of biological systems on their dynamic characteristics. Different scales of simple cuboidal (and cylindrical (models are considered for the dynamic analysis. The fundamental natural frequencies of all the models are extracted using three different approaches namely, lumped mass, finite element and numerical approaches. A relation is derived to support the effect of scaling on dynamic characteristics of cell. The results indicate that the natural frequency varies inversely with the size of the cell by a factor of 103.
References
-
Wang Liping, Hsu Hung-Yao, Li Xu, Xian Cory J. Effects of frequency and acceleration amplitude on osteoblast mechanical vibration responses: a finite element study. BioMed Research International, Vol. 2016, 2016, p. 2735091.
-
Uzer Gunes, Pongkitwitoon Suphannee, Ian Cheng, Thompson William R., Rubin Janet, Chan Meilin E., Judex Stefan Gap junctional communication in osteocytes is amplified by low intensity vibrations in vitro. PLoS One, Vol. 9, Issue 3, 2014, p. 90840.
-
Fabry Ben, Geoffrey Maksym N., Butler James P., Glogauer Michael, Navajas Daniel, Fredberg Jeffrey J. Scaling the microrheology of living cells. Physical Review Letters, Vol. 87, Issue 14, 2001, p. 148102.
-
Wee Hwabok, Voloshin Arkady Dynamic analysis of a spread cell using finite element method, mechanics of biological systems and materials. Conference Proceedings of the Society for Experimental Mechanics Series, The Society for Experimental Mechanics, Vol. 4, 2014.
-
Zarandi Marjan Molavi, Bonakdar Ali, Stiharu Ion Investigations on natural frequencies of individual spherical and ellipsoidal bakery yeast cells. Proceedings of the COMSOL Conference, Boston, 2010.
-
Maynard Robert Lewis, Downes Noel Anatomy and Histology of the Laboratory rat in Toxicology and Biomedical Research. Academic Press, 2019, p. 11.
-
Mcgarry J. G., Prendergast P. J. A three-dimensional finite element model of an Adherent eukaryotic cell. European Cells and Materials Journal, Vol. 7, 2004, p. 27-33.
-
Chandrashekara C. V., Raj Arjun S. I., Pavan Suswaram, Dharani J. Mode based frequency behaviour of a cracked beam. Vibroengineering Procedia, Vol. 19, 2018, p. 129-134.
