Abstract
Complex condition monitoring for industrial equipment is offered in this paper. The complex monitoring consists of three parts. The first part contains careful diagnostics of defects. It was greatly improved by using a new method of identification of excitation sources. This method is based on defect location with the help of remote strain gauge control and detects the exact coordinates of the detected defects. The second part covers vibration isolation of industrial equipment. For this purpose, metamaterials with quasi-zero stiffness are offered. They can almost totally isolate dynamic forces passing through them. The third part is dedicated to decrease oscillations of the equipment via dynamic absorbers. Their application can be improved by careful control of adjustment. It is offered to control the phase of oscillations on two ends of the spring.
Highlights
- Mathematical model for calculate position of defect via remote strain gauge diagnostics is made
- Special experimental equipment and computer program for data collection and analysis are made
- Concept of vibroprotection metamaterial with internal structure that provides quasi-zero stiffness is proposed
- Application of dynamic absorbers for industrial equipment with anti-phase monitoring system is proposed
1. Introduction
Industrial equipment is usually the main part of various plants. It does a great amount of useful work or creates new demand items. But reliable and durable operation of this equipment requires careful maintenance and condition monitoring.
First of all, responsible equipment requires regular diagnostics, because missed defects reduce the equipment efficiency, increase the risk of misoperation, and at worst lead to an equipment failure or even to an accident.
Some equipment requires special working conditions such as low influence of its external forces. This problem leads to the necessity to provide vibration isolation. It is very perspective for various precision equipment, CNC techniques, laboratory equipment, microscopes, etc.
The situation may be reversed: industrial equipment creates a high level of vibration. High dynamic force from the equipment can harmfully influence on all around: on other equipment, foundation, buildings and personnel. In this case, vibration of this equipment shall be carefully isolated.
Some machines have requirements to have low displacements during their work. It is relevant for the equipment connected to something, for example for pumps, compressors. In this case, it is impossible to ensure low displacement and low dynamic forces acting on the foundation using traditional vibration isolating systems. In general, hard coupling of vibrating equipment to foundation provides low displacements (vibration), but high dynamic forces, and vice versa, a vibration isolating system provides low dynamic forces transmitting from equipment to foundation, but high displacement. Simultaneous satisfaction of these two provisions creates the problem of mutual neutralization, but the usage of dynamic absorbers can help to solve this problem.
Further, some author’s ideas about a complex condition monitoring for industrial equipment is presented. This methodology contains 3 parts: a new method of diagnostics via remote strain gauge analysis, vibration isolating metamaterial with quasi-zero stiffness, high efficiency system for dynamic absorbers.
2. Diagnostics via remote strain gauge analysis
Reliable and durable operation of industrial equipment requires careful maintenance and complex condition monitoring.
It is offered to troubleshoot the industrial equipment with a help of the remote strain gauge signal analysis. The method is based on the following.
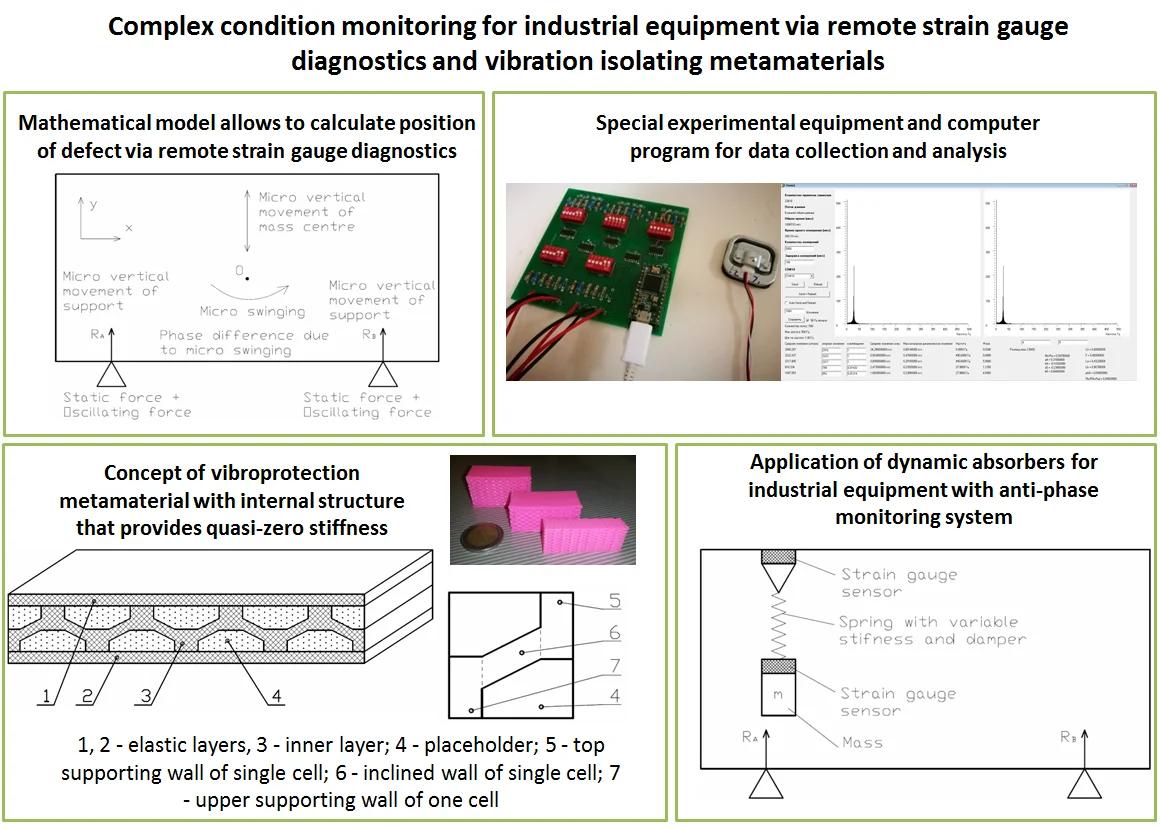
Industrial equipment is under the effect of various disturbing forces. First of all, it is rotor vibration that influences it the most. Also, bearings, connections, wheels, moving parts create disturbing forces. This set of disturbing forces makes the equipment to have micro movements (Fig. 1). Generally, the equipment has vertical micro movements and micro swinging.
Fig. 1Micro movements of equipment
Micro movements and micro swinging cause dynamic reactions on supports. These dynamic reactions can be carefully analyzed. On the basis of this information, the sources of disturbing can be located.
For this purpose, an analysis is made by strain gauges. Strain gauges are located under the supports of the rotary equipment. Strain gauges with amplifiers and microcontroller allow determining dynamic reactions to the supports in real time. If it is not possible to install them, strain gauges can be glued on the supports or equipment frame.
Equipment is usually made of steel, so it can be considered as an absolutely rigid body. Hence, the dynamic force from oscillating defects and parts completely and without loss transfers to equipment supports and strain gauges. This information may be used for the analysis of defects.
A priori, it is considered that static force, dynamic force, and phase on each support are known. A created mathematical model of machine dynamics on strain gauge sensors and its solution gives the methodology how to obtain the exact position of the sources of oscillation, in other words, to determine the defect coordinate in space, both the location in the horizontal plane (in two horizontal coordinates) and the vertical coordinate.
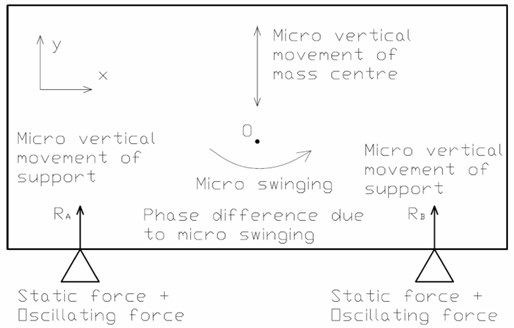
The generalized scheme of the whole diagnosis is as follows: strain gauge sensors are located between equipment and foundation. The signal from the sensors passes to amplifiers with various amplifying coefficient, then to analog-to-digital converter and further to microcontroller for collecting data. Then the signal passes to a computer where it is analyzed. Microcontroller (with integrated analog-to-digital converter), amplifiers, strain gauge sensors are presented on the Fig. 2.
One of the most principle parts of equipment is microcontroller Teensy 3.2 with integrated 12-bit analog-to-digital converter. Amplifiers are built on chip INA 125. They provide complete bridge excitation and precision differential-input amplification on a single integrated circuit. Gain may be changed from 4 to 10,000. The microcontroller requests data from 5 channels with minimum delay of 9 microseconds. The requests are made consequentially from the channels. It allows getting data with the maximum frequency of 22 kHz. The microcontroller collects data, stores it, and via COM port sends it to a computer.
For receiving and analyzing data on the computer, a program was created. For this purpose, Delphi programming language was used. The view of the program is presented on the Fig. 3.
The collected data is analyzed via Fourier transformation. Then corresponding spectrum is calculated. Generally the computer program allows doing as follows: calculating static force on each strain gauge sensors (i.e. load), calculating dynamic forces on each strain gauge sensors, (i.e. getting the amplitude and frequency of each dynamic force, presented on the spectrum), calculating phase difference relative to some reference (i.e. phase difference between dynamic forces on various strain gauge sensors).
This information due to the developed mathematical model and methodology of disturbing force identification allows calculating the defect location. Additional information such as frequency and intensity of disturbing force makes the identification of a defect more reliable.
Fig. 2Equipment for measurement strain gauge signal and its analysis

Fig. 3Computer program for data collection and analysis
3. Vibration isolating metamaterial with quasi-zero stiffness
Modern advances in the field of additive technologies make opportunities for creating of metamaterials. In particular, 3D printing can be used to create special elastic structures, in other words, to create new means of protection against vibration and shock [1, 2]. By creating various internal structures of elastic metamaterials, it is possible to impart them various force characteristics (various dependences of their restoring force on compression), including non-linear ones.
Note that elastic structures and materials with a nonlinear force characteristic with an almost flat section are called as systems with quasi-zero stiffness [3]. Such systems are currently actively developed in the field of protection against vibration and shock, since they ensure the almost complete absence of transmitted dynamic force, which makes them extremely effective for vibration isolation [4, 5]. Providing almost zero (quasi-zero) stiffness at a certain load allows simultaneously obtaining low natural frequency, wide range of isolable frequencies. It gives very high vibration isolating properties as compared with traditional vibration isolators.
Due to 3D additive technology and the use of the concept of metamaterials with quasi-zero stiffness, it is possible to create impact protection and vibration isolation systems that can be very thin and compact. One layer of material may be less than a few millimeters. In addition, the creation of a metamaterial with different layers leads to a construction with a set of special properties.
The use of such periodic structures was studied by the authors Carrella [6], Correa, Seepersad and Haberman [7, 8], Valeev, Karimov, Tashbulatov [9]. Also, metamaterials for broadband vibration isolation at low frequencies are studied by the authors Wang, Zhang, Zhang and Hu [10].
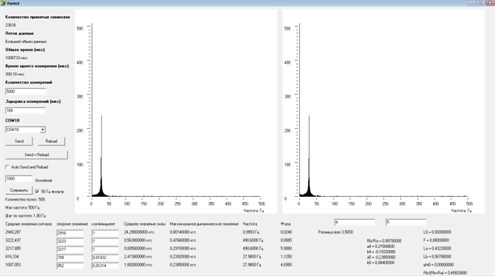
The author has developed the following vibration isolating metamaterial. It consists of two external elastic layers 1 and 2 (Fig. 4), and an inner layer. This inner layer is an elastic wave-like structure 3. The free space around it is filled with a softer elastic material 4. The elastic wave-like structure 3 and the elastic material 4 is a periodic structure of cells. So, the whole cell consists of an upper supporting wall 5, a wall 6, a lower supporting wall 7, and an elastic material 4, which fills the remaining free space.
Fig. 4Concept of vibroprotection metamaterial with internal structure that provides quasi-zero rigidity. 1, 2 – elastic layers, 3 – inner layer; 4 – placeholder; 5 – top supporting wall of single cell; 6 – inclined wall of single cell; 7 – upper supporting wall of one cell
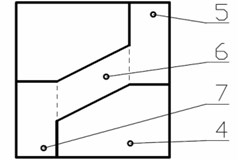
The mechanics of a single cell is the following. Wall 6 undergoes two types of deformation: bending and compression in the radial direction. The bending deformation of the wall 6 without taking into account the compressive deformation has a linear force characteristic. As the cell is deformed, the radial compression of the wall 6 increases. This leads to the fact that the wall 6 tends to return to its original position, compensating for the deformation due to bending. This option gives the non-linear force characteristic to the cell. With greater compression of the cell, the radial compression of the wall 6 reaches its maximum. The dimensions of the cell elements and the elastic properties of the upper support wall 5, the wall 6, the lower support wall 7 and the filler 4 are selected so that in this position a quasi-zero stiffness is observed. The load corresponding to this position corresponds to its working position, i.e. this load is nominal.
The cells form an elastic wave-like structure, which as a whole also possesses quasi-zero stiffness in a certain position. Consequently, this gives the offered vibration isolating metamaterial also quasi-zero stiffness.
A preliminary mathematical modeling of a single cell of the proposed metamaterial has been carried out. To check the results, a computer simulation of a single cell was performed using the Ansys software package [1, 2].
To test the feasibility of manufacturing these metamaterials, samples were produced using printing on a Picaso Designer 3D printer (Fig. 5). Elastic plastic with a Young MP modulus of 74 MPa was used. The thickness of the layers was 0.3 mm.
The study of this metamaterial is also devoted to its structure optimization. The structure shape influence the optimal static load, dynamic stiffness, damping properties and compactness (i.e. metamaterial height).
Fig. 5Demonstration samples of vibration-proof metamaterial

4. Application of dynamic absorbers for industrial equipment
A dynamic vibration damper is a device which ensures the force of inertia, reducing the level of vibrations of the protected structure. Usually, a dynamic vibration damper is provided as an additional mass, connected with an elastic and damping element to equipment. The inertial part of the absorber is usually solid. Steel springs, rubber elements, elastic rods or plates are used as elastic elements. A device consisting of a specific mass and an elastic element is attached to the mechanism, which the oscillations must be extinguished. The mass and stiffness of the vibration damper are selected so that the natural vibration frequency of the vibration damper is equal to the frequency of the forced vibration of the mechanism. During operation, the absorber becomes an additional oscillatory system that works in anti-phase with the source of oscillations. In this case, the force from the vibration damper acts against the force excited by the mechanism. As a result, the vibration damper enters into resonant vibrations, and the mechanism vibrations are reduced.
Significant counteracted forces at limited amplitudes of corrective masses can be achieved only with a relatively large mass of attached bodies, usually 5-20 % of the reduced mass.
Usually, dynamic vibration dampers are used to achieve a local effect: lowering the vibration of an object in the attachment area of the dampers.
Dynamic dampers can be constructively implemented on the basis of passive elements (masses, springs, dampers) or be active, having their own energy sources. In the second case, automatic control systems using electrically, hydraulically or pneumatically controlled elements are used. It is very convenient to apply their combination with passive devices. The use of active elements expands the possibilities of dynamic vibration damping, since it allows the continuous adjustment of the parameters of the dynamic damper as a function of the acting disturbances and, therefore, damping under conditions of varying vibration loads. A similar result can be sometimes achieved with the help of passive devices having non-linear characteristics.
Fig. 6Demonstration samples of vibration-proof metamaterial
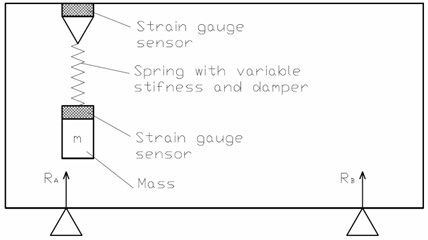
A problem of dynamic dampers strongly depends on the adjustment. If natural frequencies of the dynamic absorber and disturbing force are different then the absorber efficiency is low or even negative. For solving this problem, the following is offered. Strain gauge sensors are installed at two ends of the spring (Fig. 6). Then the monitoring of real-time signals begins, and Fourier transformation is made. For good adjustment, signals in 2 sensors should have the phase different equal to , i.e. be in the anti-phase. If there is no anti-phase then the spring stiffness must be changed. For this purpose, pneumatic springs or springs with magneto-rheological liquid can be used.
5. Conclusions
In this paper, author’s ideas to increase industrial durability and reliability are presented. They may be divided into 3 parts: a new method of diagnostics via remote strain gauge analysis, vibration isolating metamaterial with quasi-zero stiffness, a high-efficiency system for dynamic absorbers. The first one provides in-time diagnostics of defects in addition to the traditional diagnostic methods, the second one is devoted to decrease the dynamic action on foundation, and the third one is devoted to decrease the oscillations of a machine. Implementation of all three methods provides high accurate condition monitoring for industrial equipment.
References
-
Valeev A. Numerical and experimental analysis of metamaterials with quasi-zero effect for vibration isolation. AIP Conference Proceedings, Vol. 1859, 2017, p. 020061.
-
Valeev A. Vibration isolating metamaterial with arc-structure. IOP Conference Proceedings, Vol. 225, 2017, p. 012142.
-
Alabuzhev P. A., Gritchin L., Kim L., Migirenko G., Chon V., Stepanov P. Vibration Protecting and Measuring Systems with Quasi-Zero Stiffness. Hemisphere Publishing, New York, 1989.
-
Valeev A. R., Kharisov Sh. A. Application of vibration isolators with low stiffness for strongly vibrating equipment. Procedia Engineering, Vol. 150, 2016, p. 641-646.
-
Valeev A. R., Zotov A. N., Kharisov Sh. A. Designing of compact low frequency vibration isolator with quasi-zero stiffness. Journal of Low Frequency Noise, Vibration and Active Control, Vol. 34, Issue 4, 2015, p. 459-474.
-
Carrella A. Passive Vibration Isolators with High-Static-Low-Dynamic-Stiffness. Ph.D. Thesis, University of Southampton, UK, 2008.
-
Correa D. M., Seepersad C. C., Haberman M. R. Mechanical design of negative stiffness honeycomb materials. Integrating Materials and Manufacturing Innovation, Vol. 4, 2015, p. 10.
-
Correa D. M., Klatt T. D., Cortes S. A., Haberman M. R., Kovar D., Seepersad C. C. Negative stiffness honeycombs for recoverable shock isolation. Rapid Prototyping Journal, Vol. 21, Issue 2, 2015, p. 193-200.
-
Valeev A., Kolchin A., Karimov R., Tashbulatov R., Mastobaev B. Elastic suspension of rotor with quasi zero stiffness for oil pumping units. Journal of Engineering and Applied Sciences, Vol. 12, Issue 9, 2017, p. 8586-8590.
-
Wang Z., Zhang Q., Zhang K., Hu G. Tunable digital metamaterial for broadband vibration isolation at low frequency. Advanced Materials, Vol. 28, 2016, p. 9857-9861.
About this article
The reported study was funded by the Ministry of Education and Science of the Russian Federation according to the research project MK-2965.2018.8.
