Abstract
The firing accuracy of sniper rifle is significantly affected by the barrel vibration induced by shooting load. The barrel vibration is an important parameter needing to be precisely controlled, whose measurement is less studied before. The vertical vibration characteristics of sniper rifle barrel is obtained for the duration of 500 ms with high speed photography system. Both the averaged vibration frequency and maximum amplitude of the measured muzzle are gained. It is found from the test that after the appearance of the maximum value, the vibration amplitude of the muzzle reduces with nearly fixed vibration frequency. In addition, the finite element model is conducted for the barrel vibration regarding sniper rifle. And then the natural frequency as well as the vibration reflection of the barrel under the effort of shooting load is calculated with the model. The model accuracy is well validated for the numerical results are substantially in line with the measurements.
1. Introduction
In the shooting progress of high precision sniper rifle, the bullet is driven along the barrel under the effort of high pressure powder gas and flies to the target with high kinetic energy. During the progress, the barrel vibrates because of both impact action of powder gas on bore bottom and the instantaneous effort between bullet and barrel. The shooting precision can be significantly affected by the barrel vibration, and thus the research of vibration characteristics related to high precision sniper rifle has great sense to the development of sniper rifle.
There have been many references regarding to the barrel vibration excited by the bullet movement, and most of them simplified the solved equations according to the cantilever beam assumption [1, 2]. It is known that the barrel structure has obvious features like cantilever beam and using the elementary beam theory of Bernoulli-Euler, the static bending deflection of the calculated barrel, the effect of gravity on barrel bending as well as the effort of bullet motion in both constant and accelerated velocity states can be well simulated [1-4]. Such researches above give acceptable data regarding to barrel weapon like Cannon et al., but fail to accurately calculate barrel vibration of high precision sniper rifle. Unfortunately, in previous references, there is less results related to barrel vibration measurement of sniper rifle. In this paper, the barrel vibration features of sniper rifle are measured experimentally and the simulation model with high precision is also developed, which can provide method and basis for barrel design of high precision sniper rifle.
2. Experiments
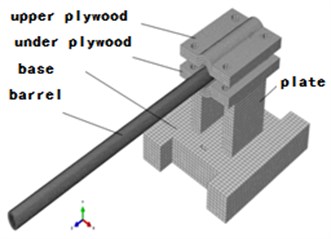
One 7.62 mm sniper rifle is shown in Fig. 1, and the clamping device, high speed camera, light source as well as PC machine are also included in experimental system. The casing of sniper rifle is fixed in the V-style clamping device, which is similar to the state that the tail of barrel is fixed with the barrel body suspended. The muzzle vibration in the shooting progress is gained with high speed camera, whose photographing frequency is 5000 frames per second with 704×304 pixel. In addition, the displacement curve of the marking point is also recorded with time.
Fig. 1Experimental objects and devices

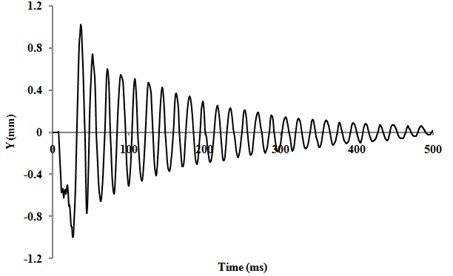
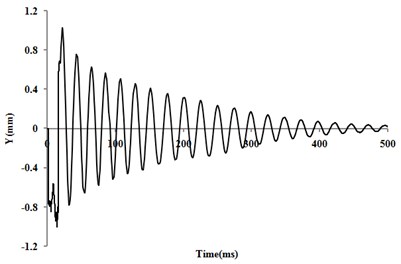
Under the same experimental conditions, multi-group muzzle vibration tests are conducted using the high speed camera, and the different results turn out to be well consist and repeatable. The typical vertical displacement curve of the muzzle is displayed in Fig. 2, which contains 500 ms displacement characteristics after the bullet left the muzzle.
It is found that the averaged vibration frequency is 52 Hz and the maximum vibration displacement is 0.99 mm. In addition, the vibration amplitude damps about 94 % in 500 ms with nearly constant frequency. It should be noted that the amplitude dissipates gradually with time, and the dissipation rate decreases gradually with time.
Fig. 2Typical vertical displacement curve of muzzle
3. Finite-element computation
3.1. Numerical model
The finite element model for simulating the muzzle vibration is built as the experimental conditions, which contains barrel, bullet and clamping device. The main grid is hexahedral element generated with reduced integration-line method. The barrel, bullet case region and lead region are dispersed to 267529 cells, 175769 cells and 110868 cells respectively. The clamping device is assembled by base, plate, upper plywood, under plywood and receiver. Total 6976 cells, 2584 cells, 7700 cells and 1000 cells are respectively meshed for base, plate, each plywood and receiver. The grid detail is illustrated in Fig. 3.
The material of copper H90 is used for bullet case, and the material of pure lead is used in bullet core. The bullet appears elastoplastic deformation under high strain during the extrusion progress, and thus it is applicable to employ J-C model to define material properties. The materials of the barrel, clamping device and casing are all high strength steel, which just considers elastic property and ignores the plastic deformation and abrasion. Some mechanical properties are listed in Table 1, and the friction coefficient between bullet and barrel is specified to 0.08. As for the surface contact types, the surface-to-surface style is adopted for the interfaces of the outer bullet case and the gun chamber, the inner bullet case and lead surface as well as the casing and the plywood. Besides, the fixed boundary is adopted for the clamping device.
Fig. 3Assemble model
a) General grid model
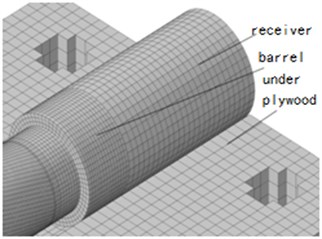
b) Inner grid assembly
Table 1Mechanical property parameters
Material | Density (kg/m3) | Young modulus | Poisson ratio | (MPa) | (MPa) |
Steel | 7.85×103 | 206000 | 0.29 | 810 | – |
Copper | 8.73×103 | 108000 | 0.35 | 160 | 620 |
Lead | 11.34×103 | 17000 | 0.42 | 11.3 | 16.5 |
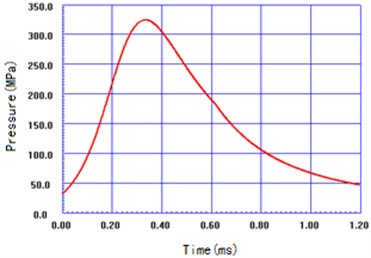
During the shooting progress, the barrel vibrates under the efforts of both the pressure pulse of powder gas and the high-speed rotatable motion of bullet, and thus the firing load is obtained from the interior ballistic model and the pressure-time curve is listed in Fig. 4. As shown, the pressure effort of powder gas is defined at bore bottom and bullet base. In addition, the ABAQUS-Explicit solver is employed to calculate the barrel vibration.
Fig. 4Firing load
3.2. Numerical results
The natural frequency and the mode are investigated for the barrel fixed at tail, and the numerical results are listed in Table 2, Fig. 5 to Fig. 7. As listed in Table 2, the natural barrel vibration frequencies are 64.7 Hz, 339.8 Hz, and 938.8 Hz respectively for the first three orders. The vibration shapes of barrel are similar to that of cantilever beam, while the measured average muzzle vibration frequency is 52 Hz, which is 19.6 % lower than that of the first order frequency, which means the stiffness of the barrel is sufficient.
The variation of muzzle vibration displacement under firing load is demonstrated in Fig. 8, and the quantitative value is listed in Table 3. As shown in Fig. 8, there are 21 wave peaks and troughs totally in 500 ms. The numerical barrel vibration frequency is 42 Hz, which underestimates the measurement 52 Hz with a relative error of 19.2 %. The maximum muzzle amplitude is 1.03 mm, which is 0.04 mm higher than the experimental data and the relative error is 4 %.
Table 2Natural barrel vibration frequencies (Hz)
Order | 1 | 1 | 2 | 2 | 3 | 3 |
Direction | Vertical | Horizontal | Vertical | Horizontal | Vertical | Horizontal |
Frequency | 64.7 | 64.7 | 339.8 | 339.8 | 938.8 | 938.8 |
Fig. 5Vertical shape of first order

Fig. 6Vertical shape of second order

Fig. 7Vertical shape of second order
Fig. 8Numerical displacement curve of muzzle
Totally, at the 1, 5 and 9 peaks, all the numerical data are close to the measurements, with relative errors of 4 %, 6.7 % and 9.9 % respectively. The numerical data agree with the measurements well in the previous 200 ms but slightly deviate the measurements in the post muzzle vibration calculation. The reason for the above phenomenon is that the muzzle displacement amplitude has been very small in the post vibration periods. Generally speaking, as for the decaying muzzle vibration calculation, the numerical data match the experiment value very well, which indicates the correctness and validity of the conducted vibration model.
Table 3Comparison between numerical and experimental data
Frequency | Maximum amplitude | 1 | 5 | 9 | 13 | 17 | |
Simulation | 42 Hz | 1.03 mm | 1.03 | 0.521 | 0.317 | 0.161 | 0.072 |
Experiment | 52 Hz | 0.99 mm | 0.99 | 0.506 | 0.352 | 0.206 | 0.126 |
4. Conclusions
1) With the high speed camera and considering the firing load, the barrel vibration characteristics of sniper rifle in 500 ms are obtained. It turns out to be that the mean muzzle vibration frequency of sniper rifle is 52 Hz, which is 19.6 % lower than the first order natural frequency. The maximum displacement amplitude of muzzle is 0.99 mm, and the amplitude is steadily reduced with nearly constant frequency after the extreme point. As the muzzle vibration energy damping, the steady reducing trend of muzzle vibration decreases gradually, concretely, the vibration amplitude drops 94 % magnitude in 500 ms.
2) A finite element model is built for the barrel vibration regarding sniper rifle, and the natural frequency as well as the barrel vibration reflection considering the effort of shooting load are presented. The numerical muzzle vibration data substantially match the measurements, verifying the accuracy of the conducted muzzle vibration model.
References
-
Hsu J. C., Lai H. Y., Chen C. K. Free vibration of non-uniform Euler-Bernoulli beams with general elastically end constraints using Adomian modified. Journal of Sound and Vibration, Vol. 318, Issues 4-5, 2008, p. 965-981.
-
Barari A., Kaliji H. D., Ghadimi M., Domairry G. Non-linear vibration of Euler-Bernoulli beams. Latin American Journal of Solids and Structures, Vol. 8, Issue 2, 2011, p. 139-148.
-
Kumar P., Nayak S. K., Datar A. M. Analysis of transverse vibration models of a gun barrel subjected to recoil. Applied Mechanics and Materials, Vol. 592-594, 2014, p. 2011-2015.
-
Mohammad T. Dynamics and stability of stepped Gun barrels with moving bullets. Advances in Acoustics and Vibration, Vol. 2008, 2008, p. 483857.
About this article
This project is supported by National Natural Science Foundation of China (Grant No. 51575279).
