Abstract
This paper investigates the estimation of foundation damping in a monopile supported offshore wind turbine. The soil-structure interaction is modelled using the commercial geotechnical Finite Element (FE) software, Plaxis 3D. This allows for a more rigorous consideration of the soil response and its effect on the overall dynamic behaviour of the system. A free vibration test is simulated by applying and removing a constant horizontal static load at the top of the tower. The structure starts free vibration when the load is removed. The free decay displacement response is measured at the point of loading. The well-known logarithmic decrement method is used for the estimation of overall damping from the free decay response. The damping is estimated at different time steps along the signal to provide an instantaneous damping. It is shown that the damping varies with the amplitude of the decaying displacement response.
1. Introduction
Development of renewable energy technologies has increased significantly over the last decade, driven by a need to prevent the effects of climate change from greenhouse gas emissions. The European Union which has set a goal of reaching at least 27 % of its total energy consumption from the renewable energy sources by the year of 2030. Offshore wind energy has played a key role in this sector as a viable clean energy source. Up until recently, the cost of offshore wind has been the main barrier for its development, however, this cost has been significantly reduced in recent years as a result of technological developments. As offshore wind moves into deeper waters, additional cost reductions are needed in terms of the economic efficiency of offshore wind structures.
As foundation for offshore wind turbines (OWTs) contribute up to 30 % of the overall cost, efficient and reliable design of these substructures can significantly reduce the cost. Monopile structures are the most common foundation type for OWTs as they are relatively easy to design, construct and install. A monopile foundation is a very large steel tube that is driven into seabed to support all the loads (weight, wind, etc.) of a large above-surface structure.
OWTs are slender structures with low natural frequencies and subjected to wind and wave loading [1]. While there is a good understanding of driving frequencies of a wind turbines dynamic response, there is limited understanding regarding the damping of these structures. Sufficient damping is critical for offshore turbines as it can limit the dynamic response and reduce the development of fatigue damage over the lifetime of the structure. Proper estimation of the damping from different sources is essential for predicting the fatigue life and optimizing the OWT design.
OWTs are subjected to a combination of damping originated from various sources. According to the literature, there are five main sources of damping in OWTs [1]:
• Aerodynamic damping.
• Hydrodynamic damping.
• Structural damping.
• Foundation (soil) damping.
• Supplemental damping provided by mechanical dissipating devices.
The total damping of the whole system is estimated as the sum of the damping from different sources. OWTs are lightly damped structures and their total damping depends on many factors and varies in a quite wide range. According to the literature, the total damping ratio is reported in a range of 1-3 % of critical damping for the turbines in the parked condition and 7-10 % for the operational condition. Among all these damping sources, soil damping is still the most uncertain damping source in OWTs.
Versteijlen et al. [2] measure vibration signals from twelve “rotor stop” – test on an OWT at Dong Energy owned – Burbo Banks wind farm. They installed an accelerometer and strain gauges along the tower to measure free decay responses. Devriendt et al. [3, 4] implemented a long-term monitoring of an OWT in Belgian North Sea. The total damping in the parked condition is estimated under various wind speed condition. They estimate that damping changes between 1.1-2.1 % when the wind speed is in a low range of 0-5 m/s, while it varies in a range of 1.5-2.6 % for wind speeds of 10-15 m/s. For higher wind speed, which create larger deflection at mudline level, higher damping values were estimated. Bajric et al. [5] employ three modal identification techniques, Eigensystem Realization Algorithm (ERA), covariance driven Stochastic Subspace Identification (COV-SSI) and the Enhanced Frequency Domain Decomposition (EFDD) for the estimation of OWT damping. They use a numerical model of an OWT in non-operation condition, where they assume the total damping is governed by structural and foundation damping. They also estimate damping from accelerations measured on a real wind turbine. The average damping is estimated about 0.7 % for the fore-aft mode and 1.2 % for the side-side mode.
Lombardi et al. [6] performed a series of laboratory tests using a scaled model wind turbine supported on a monopile in kaolin clay. They applied between 32,000 and 172,000 cycles of horizontal loading to the turbine and monitored the changes in natural frequency and damping of the model. They evaluate damping in time domain using the logarithmic decrement method. They showed that damping of the model increased with the number of cycles and higher damping variations are recorded for larger strain amplitudes in the soil. Carswell et al. [7] presents a method for finding an equivalent lumped parameter model to represent OWT foundation damping due to hysteretic energy loss. The lumped model represents the foundation damping as a viscous rotational dashpot at mudline level. They use free vibration and stochastic time history analysis using a two-dimensional finite element model. OWT foundation damping is estimated as 0.17 % to 0.28 % of critical damping to total damping using logarithmic decrement method. They also show that when OWT foundation damping is included in the model, maximum mudline moment is 7-9 % less than the case damping is not considered. The shear at mudline level also reduced by approximately 2 %.
In this paper, a 3D finite element (FE) model of an OWT is created using Plaxis 3D which is a commercial geotechnical engineering FE software. The turbine is loaded by applying a static load to create initial static deformation. The load is then released to allow the structure for free vibration using dynamic analysis. The free vibration responses are measured at several points on the structure for a relatively long time. The natural frequency of the system is estimated using fast Fourier transform (FFT) of the measured signal. The damping of the system is estimated using logarithmic decrement method from amplitudes of any two successive peaks.
2. Numerical modelling in Plaxis
The soil-structure interaction for a wind turbine is numerically modelled using Plaxis 3D 2018 software. The wind turbine is modelled at full scale in half-space as shown in Fig. 1.
Fig. 13D FE model
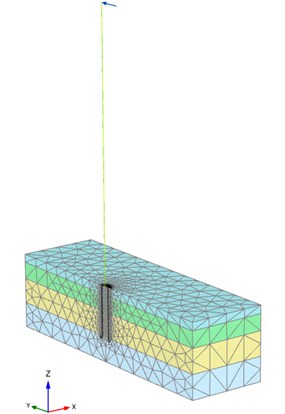
2.1. Wind turbine structure
The pile below the mudline level is modelled using linear elastic plate elements with Young’s Modulus, 210 GPa, Poisson’s ratio, 0.3 and a unit weight of 77 kN/m3. Table 1 gives the overall dimension of the monopile. Interface elements were also added to the pile shaft plate. The tower is modelled using the DTU 10-MW reference wind turbine [8]. The tower and monopile above the mudline level are modelled using linear elastic beam elements. The tower properties are given in Table 2. In order to only estimate the foundation damping, the structural damping of the system is considered to be zero.
Table 1Monopile properties
Property | Value |
Interface height above mudline (m) | 45 |
Tapered length (m) | 15 |
MP diameter at toe (m) | 8 |
MP diameter at top (m) | 6 |
MP thickness (mm) | 80 |
Table 2Tower properties
Property | Value |
Hub height (m) | 119 |
RNA mass (tons) | 675 |
Cross section area at top (m2) | 0.34432 |
Cross section area at bottom (m2) | 0.98632 |
2.2. Soil model
Four soil layers are modelled using the methodology explained in [9]. The soil elements are modelled as ten-node tetrahedral elements. The effective soil weight, is kN/m3 and the interface stiffness, is 0.7. The layers’ elevations are listed in Table 3. The mesh is then generated using Plaxis 3D’s inbuilt meshing procedure. The mesh is checked to ensure it was of sufficient quality to prevent convergence issues due to poorly constructed elements. Manual refinement of the mesh is often required to facilitate optimum numerical analysis and convergence.
Table 3Soil properties
Layer | Depth (m) | To (m) | Small strain stiffness (MPa) |
1 | 0 | 5 | 91106 |
2 | 5 | 15 | 98599 |
3 | 15 | 30 | 99405 |
4 | 30 | 45 | 99389 |
3. Damping estimation
3.1. Logarithmic decrement method
Logarithmic decrement is a method for estimating damping from free vibration time history. The logarithmic decrement of a signal is defined as the natural logarithm of the ratio of the amplitudes of any two successive peaks:
where is the amplitude of the first peak and is the amplitude of the peak periods away, where is any integer number of successive, positive peaks. The global damping ratio can then be calculated as a function of by:
which here estimates the global damping associated with the dominant mode in the signal.
3.2. Results
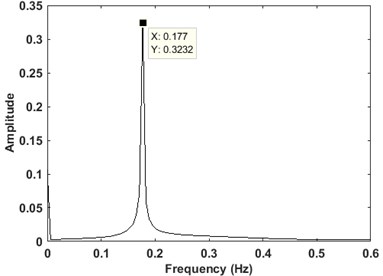
In order to create a free decay response, a point load is applied to the tower at Rotor Nacelle Assembly (RNA) level to create an initial static deflection. The load is then removed in the following phase to allow the structure to freely vibrates. Fig. 2 shows the dynamic response of the turbine measured at RNA level. Fig. 3 shows the frequency spectrum of the signal obtained from FFT. It shows a peak at 0.177 Hz corresponding to the first natural frequency of the structure. It can be seen that this mode is dominant in the signal.
Fig. 2The free decay response at RNA level
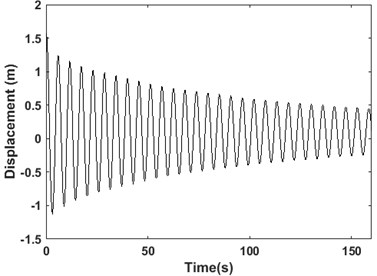
Fig. 3The FFT spectrum of the free decay response at RNA level
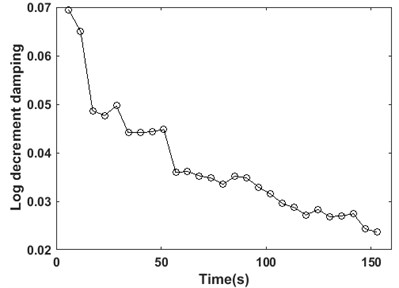
There are 28 peaks detected in the response for damping estimation. It can be seen that the amplitude of the vibration is decreasing through time. The damping values are estimated using two successive peaks in the response using the first 27 peaks as the starting points in logarithmic decrement method. The damping values are plotted versus the time instant of the first employed peak in Fig. 4. It shows that as the time passes and the amplitude of the response decreases, the overall damping of the system decreases from about 7 % to 2.5 %.
Fig. 4Logarithmic damping at different time steps
4. Conclusions
The foundation damping of an OWT on a monopile foundation is estimated using logarithmic decrement method. The free decay response of the system is measured using a numerical simulation in an FE software. The damping is calculated using different successive peaks along the signal to provide the instantaneous damping. It is concluded that the system overall damping is highly variable. It is shown that the foundation damping decreases when the structure vibrates with smaller amplitudes. This is important as damping is the only factor would limit the amplitude of the dynamic vibrations at the resonance. Therefore, accurate estimation of OWT damping plays an important role in the true estimation of its fatigue life. However, further experimental work is needed to validate the results in field tests. This can be done by installing sensors at different levels along the monopile and tower and measuring the responses.
References
-
Versteijlen W. G., Renting F. W., Van Der Valk P. L. C., Bongers J., Van Dalen K. N., Metrikine A. V. Effective soil-stiffness validation: Shaker excitation of an in-situ monopile foundation. Soil Dynamics and Earthquake Engineering, Vol. 102, 2017, p. 241-262.
-
Versteijlen W. G., Metrikine A., Hoving J. S., Smid E. H., De Vries W. E. Estimation of the vibration decrement of an offshore wind turbine support structure caused by its interaction with soil. Proceedings of the EWEA Offshore 2011 Conference, Amsterdam, The Netherlands, 2011.
-
Devriendt C., El Kafafy M., Sitter G. D., Guillaume P. Damping estimation of offshore wind turbines on a monopile foundation using state-of-the-art operational modal analysis techniques. International Conference on Noise and Vibration Engineering, 2012.
-
Devriendt C., Weijtjens W., El-Kafafy M., De Sitter G. Monitoring resonant frequencies and damping values of an offshore wind turbine in parked conditions. IET Renewable Power Generation, Vol. 8, Issue 4, 2014, p. 433-441.
-
Bajri A., Høgsberg J., Rüdinger F. Evaluation of damping estimates by automated operational modal analysis for offshore wind turbine tower vibrations. Renew Energy, Vol. 116, 2018, p. 153-163.
-
Lombardi D., Bhattacharya S., Wood Muir D. Dynamic soil-structure interaction of monopile supported wind turbines in cohesive soil. Soil Dynamics and Earthquake Engineering, Vol. 49, 2013, p. 165-180.
-
Carswell W., et al. Foundation damping and the dynamics of offshore wind turbine monopiles. Renewable Energy, Vol. 80, 2015, p. 724-736.
-
Bak Christian, et al. The DTU 10-MW Reference Wind Turbine. Danish Wind Power Research, 2013.
-
Murphy G., Igoe D., Doherty P., Gavin K. 3D FEM approach for laterally loaded monopile design. Computers and Geotechnics, Vol. 100, 2018, p. 76-83.
About this article
This publication has emanated from research conducted with the financial support of Science Foundation Ireland under Grant Number 17/IFB/5403.
