Abstract
This contribution investigates the effect of marine growth and damage severity on the modal parameters of a scaled experimental model of a monopile used in supporting offshore wind turbines. A quick glimpse of the literature review reveals that this topic has not been well investigated as the majority of previous research focuses on the effect of marine growth on the hydrodynamic loads transferred to the test structure, with little focus on its effect on the modal parameters of a structure. Nevertheless, from a monitoring standpoint, it is important to differentiate between the effect of marine growth and damage on the modal parameters, especially when these parameters are used as damage indicators, further improving existing structural health monitoring techniques in determining if the changes observed in modal parameters are caused by actual damage rather than the growth of marine organisms with time. The results provided in this contribution provide differences between the effect of marine growth and damage, which is recommended to be included in current monitoring techniques. Furthermore, a recommendation to investigate the effect of damage on damping and, possibly, the potential of using changes in damping characteristics as damage indicators is also made.
1. Introduction
Encouraged by the energy crisis and the global effort to reduce greenhouse gas emissions, renewable energy, especially wind and solar energy, have experienced rapid developments in the last three decades [1]. Such developments lead to the increase both in size and energy production capabilities of renewable energy plants. With the need for better wind conditions with lesser turbulences, wind turbines have also been deployed offshore. However, moving wind turbines offshore comes with its own set of challenges, resulting from the harsh conditions that encourage damage propagation.
With that regard, Structural Health Monitoring (SHM) techniques have been developed to track the current “health” of a structure and provide early warnings in case of damage detection [2]. In this context, damage is defined as any change in modal parameters that adversely affect the performance of the structure [3]. Amongst others, vibration-based SHM techniques are used in detecting damages mainly by monitoring the changes in modal parameters such as frequencies and mode shapes.
Offshore wind turbines are, however, subjected to Environmental and Operational Conditions (EOCs) that affect their dynamic properties. Changes in frequencies due to changing EOCs was found to sometimes exceed those caused by actual damage [4, 5].
Thus, to enhance the capabilities of structural health monitoring techniques, the effect of EOCs and damage should be clearly distinguished.
This study aims to experimentally identify the effect of marine growth and damage propagation on the modal parameters of a monopile supporting structure and try to detect key differences between changes in modal parameters resulting from marine growth, and those resulting from actual structural damage. The extraction of modal parameters was done via Stochastic Subspace Identification (SSI) using stable paths [6].
Limited work has been done with regard to identifying the effect of marine growth on offshore structures. Usually, these studies focus on the determination of the effect of marine growth on the loads imposed on the offshore structure rather than the changes in its modal characteristics.
A comprehensive review of the state-of-the-art on the impacts of marine growth on renewable energy converters is presented by Benbouzid et al. [7]. The effect of marine growth on the response of mooring lines used in floating wind turbines was studied by Spraul et al. [8].
The research of Zeinoddini et al. [9] focuses on the response of cylinders subjected to artificial marine growth. Multiple examples of the surface roughness modeling were listed and a state-of-art of experimental arrangement and methodology was provided. The cylinder was tested in a wave basin to investigate the dynamic response, especially wake dynamics, of the cylinder. A numerical model inspired by the Floatgen European project was defined and the dynamic responses of the mooring lines is computed via time domain simulations. It was found that marine growth shift the natural frequencies towards larger periods at which the floater has a larger response to wave loads. It also tends to increase the dynamic amplification factor due to the increased mass of the mooring line.
The research presented by Wei Shi et al. [10] shows the effect of marine growth with different thicknesses, densities and hydrodynamic coefficient values on the characteristics of a numerically modeled 5 MW offshore wind turbine with jacket foundation. The 5 MW turbine was taken from the benchmark turbine defined by the National Renewable Energy Laboratory (NREL) [11]. The study performs an eigen analysis and states that marine growth has little effect on the first natural frequencies but has a higher effect on the second and third.
The study of Jusoh and Wolfram [12] discussed the significant effect of marine growth on hydrodynamic loading, providing recommendations on how to prevent and remove marine growth.
A numerical analysis of marine growth effects was propsed via Schoefs et al. [13, 14] based on Response Surface Methodology. The study aimed at providing explicit approximations of load variables acting on offshore structures submitted to extreme fatigue causing events.
A laboratory-based experimental effort was undertaken by Wolfram et al. [15]. The research used real fouling to determine hydrodynamic coefficients for cylinders covered with marine growth which is considered to increase the diameter of the tubular member by a certain amount. It was found that the drag coefficient increased about 70 % higher than that for a smooth cylinder. It was also found that the marine growth effect is very important for load assessments especially the fatigue behavior of jacket structures.
The presented literature shows a limited number of studies with regard to the effect of marine growth on offshore structures. Furthermore, those studies usually focus on the effect of such marine growth on the hydrodynamic loads transferred to the structure rather than the changes to modal characteristics of such structures. The importance of investigating the effect of marine growth on modal characteristics of offshore structures can only be underlined due to the importance of differentiating between changes in modal parameters resulting from changing EOCs and those resulting from actual damage.
2. System identification
2.1. State space
The system identification utilized in obtaining the modal parameters of the laboratory based experimental structure is based on the stochastic subspace identification (SSI).
In SSI, a data matrix:
is used, which comprises of an -variant time series sampled times at a sampling rate of . At any time instant , the system output vector is .
The randomly excited discrete state space system of order can be written as:
where is the state vector, is the discrete system matrix and is the discrete output matrix. and both are zero mean white Gaussian noise terms.
The calculation of Eigenvalues and Eigenvectors is performed on a system matrix formulated in continuous time. This conversion is done by:
Using the system matrix in continuous time , the eigenvectors and eigenvalues can be calculated by solving the Eigenvalue problem:
Eigenvalues can be further used to obtain natural frequencies and damping ratios as follows:
2.2. The stochastic subspace identification
The Stochastic Subspace Identification (SSI) is a method used in estimating a stochastic state space system such as in Eq. (2). Introduced by Van Overschee and de Moor [16, 17] based on the Eigensystem Realization Algorithm (ERA) by Juang [18], it is considered a powerful tool in system identification [19].
2.3. The data driven stochastic subspace identification
The data driven SSI uses blocks of output signals stacked into a matrix, in which future row spaces are projected into the past row spaces [16, 17]. This is done via a block Hankel matrix that is built by stacking 2i data blocks with samples from as follows:
where is the referred to as the past, and is considered the future. The orthogonal projection of row spaces from onto is defined as:
where is the Moore-Penrose pseude-inverse [17].
The projection can be further decomposed to estimate the state space matrices as in [6]. A detailed derivation of the procedure can be found in [16].
2.4. Extraction of modal parameters
A problem arising when using SSI-models is to find an optimal model order, which is done via iterative estimations. Such estimations are not universally valid and would require continuous adjustment for each new experimental setup.
To overcome this problem, so-called stable paths are used. In such procedure, a large number of model orders are calculated, resulting in a number of spurious solutions. Utilizing stabilization diagrams, the obtained modal parameters are plotted versus the model order. Only those results that appear to be unchanging over several model orders are considered physical solutions and represent the modal properties of the analyzed system. There is a multitude of approaches used in identifying such stable paths as shown including Reynders [20], Allemang [21] and Magalhaes [22]. However, according to [6], those approaches rely on clustering data points which is rather expensive.
The approach adopted in this research is further detailed in [6]. In this approach, stable paths are defined to be those in which the variation of frequency, damping and Modal Assurance Criteria (MAC) are below predetermined values.
3. The experimental setup
3.1. Structure, test facility and hardware
A scaled experimental model of an offshore wind turbine monopile supporting structure, shown in Fig. 1 is used in this study.
Fig. 1Test structure and dimensions
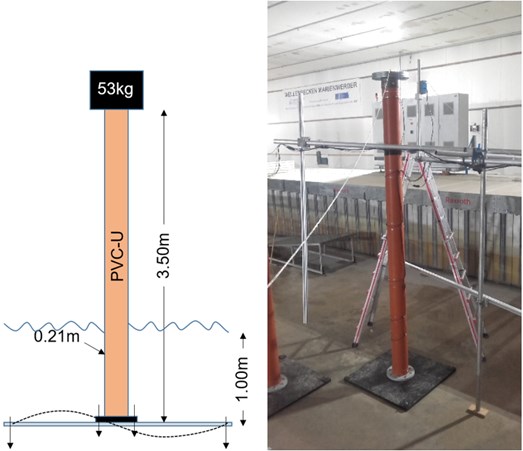
The structure consists of a 3.5 m long UPVC pipe, having a diameter of 0.21 m and a wall thickness of 5 mm. The pipe is fixed to the ground via a 1 m×1 m steel plate of 0.05 m thickness, and is fitted with a 53 kg mass on top.
The structure has a scale of 1:30 and was derived from the 5 MW benchmark turbine defined by the National Renewable Energy Laboratory (NREL). The scaling was done utilizing the Froude-Cauchy similarity criteria. The Froude criteria is usually used in hydraulic engineering when the dominant forces arise from gravitational waves. The additional consideration of the Cauchy condition is required to be able to correctly simulate the rigidity of the structure and thus the dynamic behavior of the system.
The structure is tested in a 3D wave basin shown in Fig. 2. It is 40 m long and 24 m wide, with a maximum water depth of 1 m capable of producing multi-directional sea states with a maximum wave height of around 0.47 m. The 3D wave machine (snake wave maker with 72 individual wave paddles) allows the generation of almost all required states.
Fig. 2Wave basin

The structure is fitted with 6 tri-axial accelerometers at various positions shown in Fig. 3. Furthermore, a laser-type displacement sensor is fitted at the top to measure the lateral displacement of the top mass. All measurements are conducted at a sampling rate of 500 Hz.
The application of marine growth on the structure is done via a synthetic sheet, shown in Fig. 4 of varying thickness. The specifications of the synthetic sheet are compliant with those stated in [8].
Fig. 3Sensor locations on the test structure
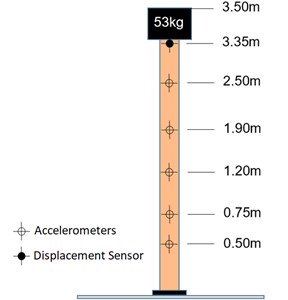
Fig. 4Synthetic sheet used as marine growth replacement

Damage was introduced via 3 symmetrically placed saw cuts at a height of 0.9 m, as shown in Fig. 5.
Fig. 5Symmetrical damage application on the test structure

3.2. Test cases
In total, 7 test setups were investigated. Three undamaged cases with increasing marine growth and 4 damaged cases with maximum marine growth.
The marine growth cases can be detailed as follows: a growth free case, an intermediate growth case, simulated by 1 layer of the synthetic and finally, a severe growth case simulated by 3 layers.
Furthermore, 5 cases of damage severity were investigated. A damage free case, in which no saw cuts were introduced, and damaged cases having a saw cut depth of 2 mm, 7 mm, 12.5 mm and 25 mm.
All damaged cases were coupled with the most severe marine growth case. This allows to test a structure having both marine growth and damage, providing means to distinguish between changes caused by marine growth and those caused by damage. Furthermore, damage usually happens at a later stage of the lifespan of a structure, in which it is safe to assume that marine organisms have already grown on the structure.
Waves are generated according to the JONSWAP spectrum [23]. To generate the waves via the JONSWAP spectrum, multiple inputs have to be provided, especially average wave height and wave period. Due to mechanical limitations of the wave generator, larger waves cannot be generated at higher frequencies due to mechanical limitations of the wave generator.
For each test setup, a minimum of 500 waves are generated to achieve a good statistical distribution. Furthermore, each test setup is carried out 5 times.
Before wave tests were performed, a free vibration tests was done. This involves pulling a cable connected to the top mass to a predetermined displacement (20 mm and 30 mm), then releasing the cable allowing the structure to vibrate freely. Such tests can estimate the first eigenfrequency of the structure, which is used to calibrate the period of the generated waves.
Wave tests of varying wave heights and periods are shown in Table 1. The periods were chosen to be multipliers of the first eigenfrequency of the test structure.
A summary of the considered test setups is shown in Table 2.
Table 1Wave heights and periods
Wave height (cm) | Wave period (sec) |
5.00 | 1.02 |
7.50 | 1.02 |
22.50 | 2.04 |
27.50 | 3.06 |
Table 2Test setups: characteristics of the tested structure
Setup | Marine growth | Damage |
1 | No | No |
2 | 1 Layer | No |
3 | 3 Layers | No |
4 | 3 Layers | 3×2 mm cuts |
5 | 3 Layers | 3×7 mm cuts |
6 | 3 Layers | 3×12.5 mm cuts |
7 | 3 Layers | 3×25 mm cuts |
4. Results
The previously described tests are carried out and analyzed via data driven SSI using the stable paths method.
The data driven SSI obtains the damping of the model for a variety of frequencies and SSI model orders. There are many non-physical eigensolutions for the system resulting from a variety of sources such as noisy measurements, wave generator movement, wave generator RPM and measurement filtering. Thus, data driven SSI should detect physical from nonphysical frequency and damping parameters. Physical parameters are those which do not change significantly when different model orders are used.
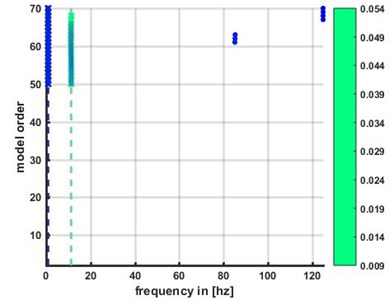
Since the number of tests is large, an example of the identified modal parameters using SSI is shown in Fig. 6, which depicts a 3-dimensional non-filtered plot of frequency, damping and model order. Those data are further filtered according to the stable path criteria and shown in Fig. 7.
Fig. 6An example of obtained frequencies and damping via data driven SSI
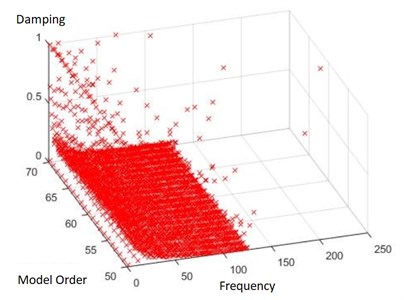
Fig. 7An example of determining feasible solutions via stable paths
4.1. Free vibration tests
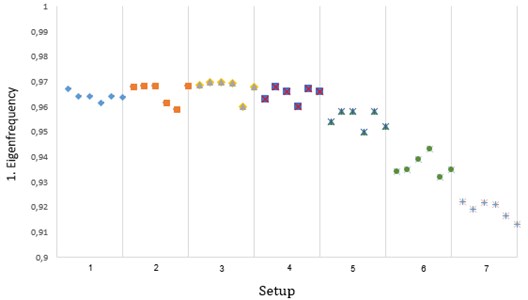
The results with regard to the first frequency are shown in Fig. 8. Two significant observations can be made with regard to the effect of marine growth and damage severity on the first frequency.
On one hand, the thickness and extent of modeled marine growth has no observable effect on the first frequency. This can be due to the shape of the first mode, where the largest displacements are situated at the tower top.
On the other hand, a clear effect of damage on the first frequency is observed. There is a downward trend in which the frequency does decrease when the damage severity is increased.
Fig. 8First frequency obtained via SSI utilizing stable paths (free vibration tests)
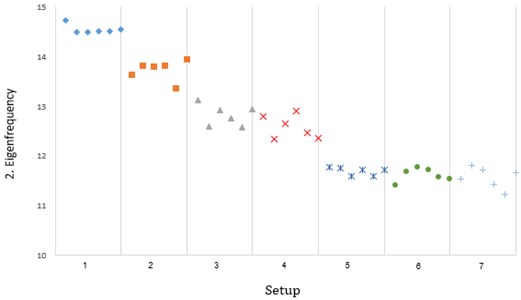
For the second frequency, the results are shown in Fig. 9. It is interesting to note that marine growth has a notable impact on the second frequency of the test structure. This can be attributed due to the fact that the second mode has a larger displacement at the position of the marine growth, which typically occurs near the water line where oxygen and sunlight levels allow such growth.
Furthermore, there is no notable change between an undamaged and damaged test structure with regard to the second frequency. There is, however, a jump between the 2 mm and 7 mm damage scenarios, resulting from water flowing into the test structure, as the wall thickness is 5 mm and is already breached when a 7 mm damage scenario is introduced.
Fig. 9Second frequency obtained via SSI utilizing stable paths (free vibration tests)
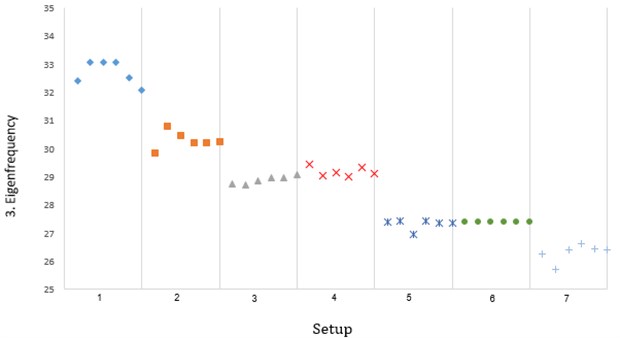
As for the third mode, shown in Fig. 10, similar observations may be drawn: marine growth has an impact on the frequency whilst damage has not. Furthermore, the same jump between the 2 mm and 7 mm damage scenarios exists.
Fig. 10Third frequency obtained via SSI utilizing stable paths (free vibration tests)
4.2. Wave tests
In these tests the structure is subjected to approximately 500 waves generated via the JONSWAP spectrum.
In comparison with the results of the tests under free vibration circumstances, the results of tests utilizing generated waves have a higher deviation. This is also attributed due to the interaction between generated waves and the test structure.
Nevertheless, the findings that were reported in the free vibration tests are still valid in the case of wave tests.
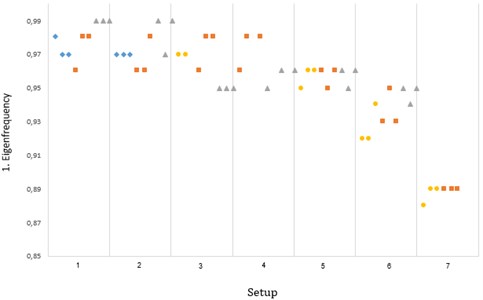
For the first frequency, shown in Fig. 11, damage had a more significant effect than marine growth.
Fig. 11First frequency obtained via SSI utilizing stable paths (wave tests)
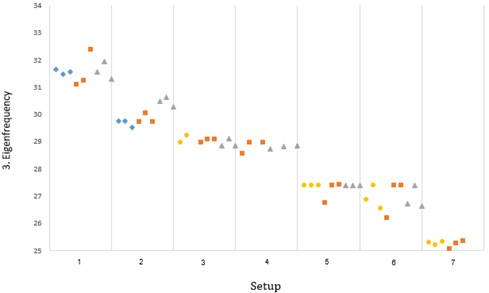
For the second frequency, shown in Fig. 12 as well as the third frequency shown in Fig. 13, marine growth had a higher effect than damage.
The smaller effect of marine growth, which is applied near the water line where oxygen and sunlight levels are just right, on the first frequency can be due to the shape of the first mode, where the largest displacements are situated at the tower top. The shape of the second and third modes are also responsible for the higher effect of marine growth on those modes.
Fig. 12Second frequency obtained via SSI utilizing stable paths (wave tests)
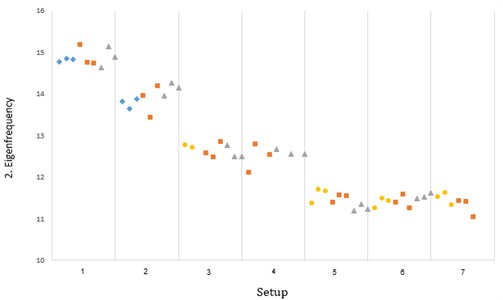
Fig. 13Third frequency obtained via SSI utilizing stable paths (wave tests)
The step change between 2 mm and 7 mm damage cases still exists as water pours inside the test structure when saw cuts exceed 5 mm.
4.3. Damping
The identified damping for the first three modes is shown in Table 3. It is noteworthy that damage has a smaller impact on damping than marine growth. Although there exists studies that do not agree with this outcome, the damping ratio was found to be insensitive to damage. This is due to the artificial nature of damage itself, as it is introduced via saw cuts rather than cracks. Natural cracks to create new energy dissipation paths via friction that increase the damping of the structure. On the contrary, damaging a structure via saw cuts does not generate the same friction effect. Thus, it is expected for saw cuts not to affect the damping characteristics of the test structure.
Table 3Test setups: characteristics of the tested structure
Setup | Damping (%) | ||
1st mode | 2nd mode | 3rd mode | |
1 | 1.09 | 1.47 | 1.15 |
2 | 1.18 | 2.35 | 1.29 |
3 | 1.17 | 2.34 | 1.34 |
4 | 1.23 | 2.33 | 1.74 |
5 | 1.25 | 2.26 | 1.61 |
6 | 1.25 | 2.06 | 1.59 |
7 | 1.25 | 2.06 | 1.63 |
5. Conclusions
The presented research investigates the effect of marine growth and damage on the modal characteristics of a scaled laboratory model of a monopile supporting structure used in offshore wind turbines. Not much literature exists that covers the topic, since the majority of previous research focuses on the effect of marine growth on the hydrodynamic loads transferred to the test structure. The novelty of this research is the fact that it present an experimental investigation with the purpose of distinguishing between the effect of damage and marine growth on the modal parameters of offshore wind turbine supporting structures, providing important clues that improve current structural health monitoring procedures and aid in differentiating changes in modal parameters that are resulting from actual damage from changes that result from the growth of marine organisms on the monopile structure.
It was found that damage is most likely to be detected when observing the first mode, since lateral displacements are maximized at the tower top and damaging the structure will inadvertently increase those lateral displacements.
On the other hand, marine growth was found to be detectable when observing the second and third modes, as those modes have higher lateral displacements near the water line, the location where marine growth was introduced.
Damping was found to increase with the application of marine growth, which is expected as marine growth tends to increase surface roughness and provide an additional energy dissipation mechanism that increases damping.
The findings support the research provided in [24]. Although a different structure, it was still tested in a wave basin with marine growth. The findings also provided hints that hydrodynamic forces are increased in the presence of marine growth and also hinted to possible changes in frequencies. The novelty of this research is that it actually distinguishes between the effect of marine growth and damage and provides clues and hints for structural health monitoring frameworks that aid in correctly detecting damage without obtaining false-positives resulting from marine growth.
Damage was found to have an insignificant effect on the damping characteristics of the test structure. Still, this fact should be considered with caution, as the damage application method was somehow artificial via introducing saw cuts of prescribed depth. Such saw cuts do not create additional internal friction that would further dissipate energy thus does not increase damping.
In reality, damage is due to the accumulation of micro cracks and fatigue. Such micro cracks create interfaces that do dissipate energy via friction and are considered to increase damping.
Thus, it is encouraged to investigate the effect of damage on damping and, possibly, the potential of using changes in damping characteristics as damage indicators.
Furthermore, model-updating could prove to be a useful method in not only detecting damage as presented in this investigation, but to even locate damage and quantify it as well.
References
-
International Wind Energy Development: Offshore Report 2010. Technical Report, BTM Consult ApS, Ringkøbing, Denmark, 2010.
-
Sohn H., Farrar C. R., Hemez F. M., Czarnecki J. J. A Review of Structural Health Monitoring Literature: 1996-2001. Structural Health Monitoring, LA-13976-M, 2004.
-
Khoshnoudian F., Esfandiari A. Structural damage diagnosis using modal data. Scientia Iranica, Vol. 18, Issue 4, 2011, p. 853-860.
-
Roohollah Talebitooti, Zarastvand Mohamadreza, Rouhani A. H. Investigating hyperbolic shear deformation theory on vibroacoustic behavior of the infinite functionally graded thick plate. Latin American Journal of Solids and Structures, Vol. 16, Issue 1, 2019, p. e139.
-
Roohollah Talebitooti, Johari Vahid, Zarastvand Mohamadreza Wave transmission across laminated composite plate in the subsonic flow investigating two-variable refined plate theory. Latin American Journal of Solids and Structures, Vol. 15, Issue 5, 2018, https://doi.org/10.1590/1679-78254352.
-
Moritz Häckell W., Rolfes Raimund Monitoring a 5MW offshore wind energy converters: condition parameters and triangulation based extraction of modal parameters. Mechanical Systems and Signal Processing, Vol. 40, Issue 1, 2013, p. 322-343.
-
Benbouzid Hosna Titah, Benbouzid Mohamed Biofouling issue on marine renewable energy converters: a state of the art review on impacts and prevention. International Journal on Energy Conversion, Vol. 5, Issue 3, 2017, p. 67.
-
Spraul C., Pham H.-D., Arnal V., Reynaud M. Effect of marine growth on floating wind turbines mooring lines responses. 23rd Congrès Français de Mécanique, 2017.
-
Zeinoddini M., Bakhtiari A., Ehteshami M., Seif M. S. Towards an understanding of the marine fouling effects on VIV of circular cylinders: Response of cylinders with regular pyramidal roughness. Applied Ocean Research, Vol. 59, 2016, p. 378-394.
-
Shi Wei, Park Hyun Chul, Baek Jae Ha, Kim Chang Wan, Kim Young Chan, Shin Hyun Kyoung Study on the marine growth effect on the dynamic response of offshore wind turbines. International Journal of Precision Engineering and Manufacturing, Vol. 13, Issue 7, 2012, p. 1167-1176.
-
Jonkman J., Butterfield S., Musial W., Scott G. Definition of a 5-MW reference wind turbine for offshore system development. Technical Report February, National Renewable Energy Laboratory, Colorado, USA, 2009.
-
Jusoh I., Wolfram J. Effects of marine growth and hydrodynamic loading on offshore structures. Jurnal Mekanikal, Vol. 1, 1996, p. 77-98.
-
Schoefs Franck Sensitivity and uncertainty studies for the modelling of marine growth effect on offshore structures loading. 21st International Conference on Offshore Mechanics and Arctic Engineering, 2002, p. 275-281.
-
Schoefs Franck, Boukinda Morgan Modelling of marine growth effect on offshore structures loading using kinematics field of water particle. International Offshore and Polar Engineering Conference, Vol. 1, 2004, p. 419-426.
-
Wolfram J., Theophanatos A. OTC 4954 The effects of marine fouling on the fluid loading of cylinders: some experimental results. Offshore Technology Conference, 1985.
-
Overschee Peter Van, Moor Bart De Subspace algorithms for the stochastic identification problem. Automatica, Vol. 29, Issue 3, 1993, p. 649-660.
-
Overschee P. V., Moor B. D. Subspace Identification for Linear Systems. Kluwer Academic Publischers, Dordrecht, Netherlands, 1996.
-
Juang J.-N. Applied System Identification. Prentice Hall, Englewood Cliffs, 1994.
-
Brincker Rune, Andersen Palle Understanding stochastic subspace identification. Proceedings of the 24th IMAC, 2006, p. 279-311.
-
Reynders Edwin, Houbrechts Jeroen, Roeck Guido De Fully automated (operational) modal analysis. Mechanical Systems and Signal Processing, Vol. 29, 2012, p. 228-250.
-
Allemang R., Brown D., Phillips A. Survey of modal techniques applicable to autonomous/semi-autonomous parameter identification. International Conference on Noise and Vibration Engineering, 2010.
-
Magalhães Filipe, Cunha Álvaro, Caetano Elsa Online automatic identification of the modal parameters of a long span arch bridge. Mechanical Systems and Signal Processing, Vol. 23, Issue 2, 2009, p. 316-329.
-
Klaus Hasselmann, et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergänzungsheft, 1973.
-
Jannis Landmann, et al. Laboratory Tests on Wave Forces and Accelerations of a Three-Bay Long-Line Aquaculture Systems in Offshore Conditions. The 29th International Ocean and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2019.
