Abstract
To formulate a plan of maintenance, the key aspect is to determine the maintenance intervals, as the maintenance types and maintenance intervals of each system are provided in the maintenance plan, and the types of each system are usually fixed. In this paper, the using data of aircraft components was employed to determine the maintenance interval. The least-squares method was adopted to estimate the Weibull distribution parameter. Then, the maintenance task interval model was set up. At last, the method was verified by using the reliability data of landing gear in in CESSNA172R.
Highlights
- Based on the method of reliability analysis, the reliability life under different fault influence categories is obtained as the recommended value of maintenance interval.
- By using the existing maintenance interval method, a method of determining the maintenance task interval was put forward for school training aircraft maintenance.
- By using the school training aircraft maintenance history data, a model was established and verified.
- It was verified by using the reliability data of landing gear in in CESSNA172R, which is used to demonstrate the rationality of this method.
1. Introduction
To formulate reasonable maintenance tasks and maintenance intervals for the aircraft system components is the MSG-3 analysis purpose, but only some guiding ideology and frame processes were provided by MSG-3. In the practice of maintenance planning, it is still necessary to adopt relevant maintenance optimization models or similar types of experience, so as to determine the component maintenance interval [1-3]. However, to determine the maintenance interval in using the former, the core problem concerns the part of the life distribution of each component. Therefore, just by making sure the parts of the component life distribution number, the reasonable maintenance interval can be calculated.
Normal fault distribution mainly includes the index distribution, normal distribution and Weibull distribution. Among them, the most widely used way in the field of maintainability is Weibull distribution. At present, the diagram parameter estimation method is based on engineering practice, when Weibull distribution parameter estimation is the most commonly used method, because this method is not only easy to use, and straightforward, but also can be applied in the truncated life tests. However, its drawback is that the result is always not so accurate. Besides, the methods based on engineering will often meet the small capacity sample situation, which made it difficult to apply [4-6]. Therefore, in view of the above questions, this paper [7] introduced two parameters Weibull distribution and shape parameter , and the characteristics of life parameter of the point estimation. Then, according to its component life distribution, the component maintenance interval is determined.
2. Weibull distribution
The failure distribution function that obeys Weibull distribution is:
where, , 0; and refer to the scale parameter and the shape parameter respectively.
Its reliability function is:
The density function is:
The failure rate function is:
3. The median rank and the least-squares method
In this paper, by using the median rank and the least-squares method, two parameters, namely and are estimated.
Suppose school training aircraft certain parts of use reliability data {, 1, 2, …, }, and there are , to times a median rank:
At this time, to obey Weibull distribution of the distribution function also can change the form:
They can also change into the linear form. Among them:
Among them: , , .
By adopting the least-squares method, according to , conducts parameter estimation, and it can get:
when the confidence size is , the life the confidence lower limit for: make . The function degree of confidence is , and by obeying Weibull distribution, the average life expectancy of the unilateral confidence lower limit is estimated as :
In this again to to , when getting confidence , the average life expectancy of the bilateral confidence limit is estimated as and :
In addition, the linear correlation degree of two variables , can be expressed as correlation coefficient :
Its scope is: 1.
Therefore, if 1, it means perfect correlation. In other words, when the variable is between and , function relations exist; If 0, it represents zero correlation, and there is no relationship between and ; If is between 0 and 1, it represents statistical correlation and that is what we related. In addition, the more is subject to Weibull distribution, the more the demand for correlation coefficient approaches to 1 [8].
4. The fixed maintenance interval
Timing maintenance mainly includes the timing overhaul type and the timing scrap type. In the modeling process, if the product regular overhaul later assumed its repair such as the new, the maintenance strategy from the perspective, timing overhaul work and timing scrapped working in MSG - 3 basic no difference can be seen as timing update maintenance. Therefore, they can be the same maintenance model [9, 10].
According to the given fault probability of occurrence for determining the timing overhaul and the timing scrapped interval, the requirements of the safety level can be guaranteed.
After a variety of maintenance interval guarantee models and the international mainstream models on the comprehensive research of PPH, according to the civil aviation school of china in CESSNA172R PPH maintenance tasks and interval formulation methods and in the use of engineering experience, in view of the failure approximation of functions or in accordance with two parameters, the fault impact type maintenance program identification maintenance interval equation is expressed as:
where refers to the maintenance project fault impact category.
5. Examples
As the classic of CESSNA172R, CESSNA is currently the world’s largest aircraft production, and it has the greatest number of the general aviation aircraft at home. The main user is CESSNA172R China civil aviation administration directly under the cultivation of the civil aviation pilots and other professional and technical personnel of the higher school, and nowadays, this machine is the largest primary trainer at home, and is effectively used for pilot performance training [11].
Teaching practice is the main purpose of the training aircraft. Usually, flying cadets should go through the tertiary trainer for more training subjects. The training aircraft landing gear system has the following use characteristics:
(1) As for the landing gear system, frequently CESSNA172R is taken as an example. The daily average landing number is 20 times, when most numbers are up to 50 times;
(2) As students’ flight experience and technical level are limited, the aircraft is always not smooth, and the heavy landing phenomenon even appears;
(3) The reliability of the landing gear system is lower than that of the large transport aircraft.
Above factors resulted in failure that often appears in the training aircraft landing gear system, and the fault. The percentage is higher than that of most transport aircraft landing gear systems. The fault statistics of three aircraft landing gear systems concerning Initial teaching machine 172R, the teaching of machine PA44 and higher education machine PA42 of Civil Aviation Flight University of China are shown in Table 1.
Table 1The fault percentage of three training aircraft landing gear systems of Civil Aviation Flight University of China
Type | Start-stop time | The machine fault number | Landing gear failure number | Percentage |
172R | 2010.03-2018.03 | 1668 | 99 | 5.94 % |
PA44 | 2010.01-2018.03 | 2354 | 415 | 17.63 % |
PA42 | 2010.05-2018.03 | 1218 | 135 | 11.08 % |
According to reference [12], with 172R landing gear maintenance history data as an example, through data processing, the obtained data is shown in table 2. This example of fault impact categories has six categories.
Table 2The failure interval of the 172R landing gear system
Serial number | MTBF (FH) | Serial number | MTBF (FH) | Serial number | MTBF (FH) | Serial number | MTBF (FH) |
1 | 3.20 | 2 | 3.30 | 3 | 4.20 | 4 | 5.90 |
5 | 6.20 | 6 | 6.90 | 7 | 11.50 | 8 | 10.60 |
9 | 13.80 | 10 | 13.00 | 11 | 21.70 | 12 | 23.30 |
13 | 26.50 | 14 | 28.50 | 15 | 36.00 | 16 | 49.20 |
17 | 48.80 | 18 | 74.00 | 19 | 74.15 | 20 | 79.40 |
21 | 83.50 | 22 | 91.70 | 23 | 94.10 | 24 | 97.60 |
25 | 130.75 | 26 | 135.20 | 27 | 140.60 | 28 | 149.20 |
29 | 148.48 | 30 | 151.00 | 31 | 154.10 | 32 | 167.80 |
33 | 190.32 | 34 | 223.00 | 35 | 241.20 | 36 | 245.60 |
37 | 257.00 | 38 | 268.00 | 39 | 271.00 | 40 | 272.00 |
41 | 276.10 | 42 | 290.00 | 43 | 290.70 | 44 | 290.50 |
45 | 290.50 | 46 | 306.50 | 47 | 330.10 | 48 | 349.70 |
49 | 351.50 | 50 | 381.00 | 51 | 412.20 | 52 | 448.00 |
53 | 603.00 | 54 | 649.50 | 55 | 740.20 | 56 | 857.70 |
57 | 895.40 | 58 | 1040.50 | 59 | 1142.40 | 60 | 1250.50 |
61 | 1594.50 | 62 | 1740.00 | 63 | 2012.50 | 64 | – |
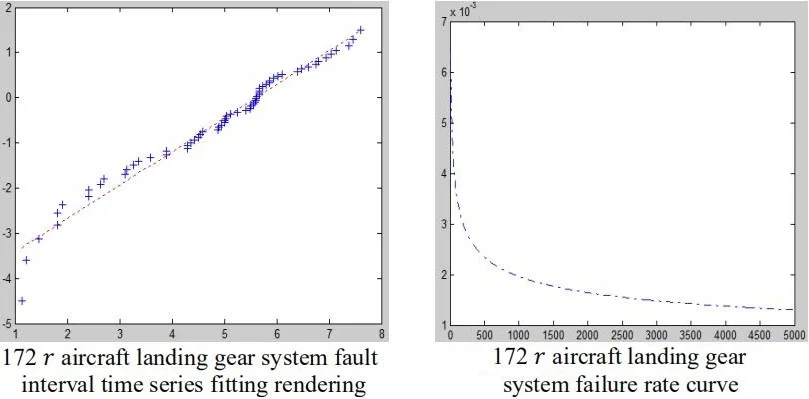
This paper makes use of MATLAB software to realize the above algorithm. According to the parameter estimation method, it 272.0551, 0.7359, and 0.9849 can be calculated. For the fitting line, 0.7438-4.1703. Combined with Table 2, fitting effect is shown in Fig. 1. From Fig. 1, we can directly see the basic data point along the fitting line distribution, and the specification of using two parameters’ Weibull distribution theory for fitting the 172R aircraft landing gear system fault interval time sequence is feasible.
The CESSNA 172R aircraft landing gear system failure rate function is , and the curve of the failure rate is shown in Fig. 2.
From Fig. 2, it can be seen that before about 500 FH, the 172R aircraft landing gear system failure rate is larger, and at the same time, this phase of the plane failure rate decline is faster, and the curve is steep; after 500 FH, the failure rate decline slowed, and there is a smooth curve with the downward trend.
In addition, according to Eq. (15), we can get the project maintenance interval, 540 FH. As school maintenance engineering considers its own maintenance ability and aircraft operating environment, it will adjust the checking interval to 500 FH, and the maintenance interval has been used for many years.
Fig. 1172 r aircraft landing gear system fault interval time series fitting rendering
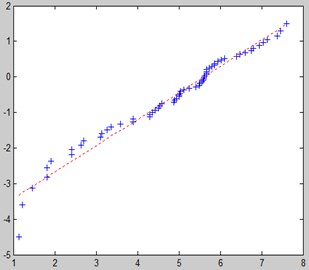
Fig. 2172 r aircraft landing gear system failure rate curve
6. Conclusions
1) Based on the method of reliability analysis, and through statistical inference of reliability life, the reliability life under different fault influence categories is obtained as the recommended value of maintenance interval, which provides a reference for the determination of maintenance interval of aircraft system.
2) By using the existing maintenance interval method, a method of determining the maintenance task interval was put forward for school training aircraft maintenance. In addition, by using the school training aircraft maintenance history data, a model was established and verified.
3) Finally, it was verified by using the reliability data of landing gear in in CESSNA172R, which is used to demonstrate the rationality of this method. This method not only is a kind of existing method for supplement, but also provides a simple and practical engineering method.
References
-
Luo Bin Research on Fleet Maintenance Decision-making based on Structure Fatigue Life Prediction. Ph.D. Thesis, Harbin Institute of Technology, Harbin, 2018.
-
Wang Xiao Bing Research on Civil Aviation Engine Maintenance Interval Optimization Based on Hole Detection. Ph.D. Thesis, Civil Aviation University of China, Tianjin, 2018.
-
An Di-Sen Research on Interval Optimization Method for Imperfect Preventive Maintenance Task. Ph.D. Thesis, Civil Aviation University of China, Tianjin, 2018.
-
Jia Bao-Hui, Sun Rong-Rong, Wang Yu-Xin Study on determining the maintenance task interval of civil aircraft system. Machinery Design and Manufacture, Vol. 2, Issue 2, 2017, p. 145-148.
-
Cui Yi-Yong, Zhai Qing-Gang Research on the calculation method for the maintenance interval of airborne products. International Conference on Information and Automation, Vol. 7, 2014, p. 1250-1254.
-
Diao Hai-Fei Research of Comprehensive Maintenance Task Optimization Method Based on Similar Models Data. Nanjing University of Aeronautics and Astronautics, Nanjing, 2014.
-
Wang Yong, Xu Zhi-Feng, Wang Ying The principle of MSG-3 systems failure effect analysis. Aviation Maintenance and Engineering, Vol. 2, 2013, p. 71-74.
-
Zuo Hong-Fu, Cai Jing, Wu Hao Aviation Maintenance Engineering. Science Press, Beijing, 2011.
-
Cai Jing Civil Aircraft System Maintenance Planning Method Research. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, 2007.
-
Sheng Zhou, Xie Shiqian, Pan Chengyi, et al. Theory of Probability and Mathematical Statistics. 4th Edition, Higher Education Press, Beijing, 2008.
-
Venus, Chen Jingpeng, Wen Ming, et al. Weibull distribution product parameter estimation maximum likelihood optimization method. Journal of Equipment Command Technical College, Vol. 5, 2003, p. 46-48.
-
Wang Lei Based on the Reliability of the Civil Aircraft Maintenance Interval to Determine the Model Method Research. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, 2007.
About this article
The author gratefully acknowledges the support from the Binzhou University Scientific Research Fund (Project No. BZXYG1705) and Binzhou University Double Service (Project No. BZXYSFW201813).
