Proposition of stiffness reduction in analysis of clay brick masonry under cyclic/seismic loads

2.1. Theoretical considerations

In engineering practice as well as in standards, masonry is usually treated as an isotropic material with linear-elastic characteristics. In case of the experimental determination of the modulus of elasticity $E$, (based on the standard EN 1052-1 [12]) the problem of determining the value of the modulus of elasticity is then reduced to determining the tangent of inclination angle of the secant stress-strain relationship in the interval (usually from $\sigma =$ 0 to $\sigma =$ 0.33${\sigma }_u$ where ${\sigma }_u$ is the maximal value of compressive stresses – peak value), to the axis of deformation. Eurocode6 [1], like other European standards, determines this value as an initial modulus of elasticity. The limits of the range may be different, e.g. in the Scandinavian countries, a secant modulus in the range of stresses from $(\sigma =$ 0.1 ${\sigma }_u$) to ($\sigma =$ 0.4 ${\sigma }_u$) was usually determined.

In the absence of experimental data, Eurocode 6 [1] allows to determine the value of an ad hoc modulus of elasticity from the following relationship:

where $K_E$ is the coefficient depending of type of masonry units (specified in National Annexes or taken as table value given in [1]; in case of masonry made of clay solid bricks usually is taken $K_E=$ 1000), and $f_k$ is the characteristic compressive strength of masonry (taken from tests carried out with the accordance with [12] or from the National Annex).

Obviously, such determined modulus of elasticity describes the behaviour of masonry as typical isotropic body, whereas the real behaviour of masonry is non-linear elastic-plastic with brittle failure. As stress builds up in the masonry, the value of Young’s modulus is changing due to the partial plasticity of the material and the development of micro cracks. According to the concepts of Continuum Damage Mechanics (see e.g. Murakami [13]), the effective stiffness represented by the value of Young’s modulus is changing by the variation of the damage variable $D_c$:

where $D_c$ is the damage variable from the range (0 ≤ $D_c$ ≤ 1) and $E_0$ is the initial value of the modulus of elasticity for the elastic behaviour of the material. In case of masonry structures the $E_0$ value is taken as the tangent of inclination angle of the secant stress-strain relationship in the interval from $\sigma =$ 0 to $\sigma =$ 0.33 ${\sigma }_u$ where ${\sigma }_u$ is the maximal value of compressive stresses.

The damage factor $D_c$ is depending on the level of the internal compressive stresses and non-elastic behaviour of masonry. This is particularly evident in the case of cyclically compressed walls, where changes in material properties are mainly caused by the development of micro cracks. As a result, along with the increase of the state of stress and deformation of the wall, the value of the elastic modulus decreases abruptly – see Fig. 1 (taken from [14]).

Fig. 1Change of the elastic (secant or current) modulus of elasticity E of uniaxial cyclic compression of masonry wallettes as a function of a strain in vertical direction

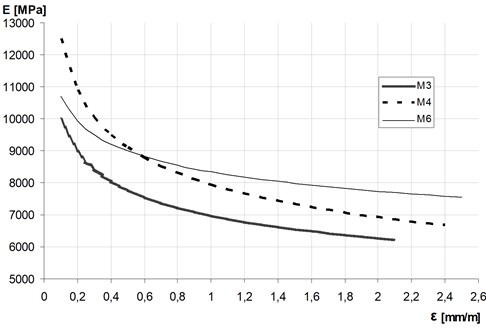
In case of masonry under axially cyclic compression, the damage variable $D_c$ usually is not a linear function of the strain – see Galman and Kubica [14]. The critical value of the damage variable $D_c$ is 0.5 and is generally reached at the point of fracture of the masonry sample. In case of masonry it is corresponding with the state of the visible cracks with width exceeding 3 mm. The theoretical maximum value is one and is corresponding with the state of failure connected with the fully destruction of the masonry. Therefore, in analytical and numerical calculations it is advisable to take the effective value of the modulus of elasticity, determined from the Eq. (2) for the appropriately calibrated value of damage parameter $D_c$.

2.2. Test’s data and discussion of the problem

To verify the behaviour and changes of the mechanical properties of masonry made of solid clay bricks strength class “30” ($f_b=$ 30 MPa) and the most wide being in use, cement-lime mortar (1:1:6) strength class M5 research work were carried out by Galman [15] at the Department of Structural Engineering of the Silesian University of Technology in Gliwice. Partially, the results were presented in Kubica et al. [16]. Research programme has consisted of four series of wall specimens of shape and overall dimensions as shown in Fig. 2(a). Masonry wallettes had thickness 25 cm and English bond, which is typical and the most popular in Poland. First specimen, naming as MW-d were the reference number and was subjected to axially compression in one cycle. The other three series included specimens subjected to axially cyclic compression. Elements of series MW-c were loaded cyclically from zero up to failure with gradation of loading force in every cycle every 150 kN and unloading in any cycle to zero. In case of series MW-c-0.33 the compressive force also increased every 150 kN but after firs three cycles the unloading was realize up to the 1/3 of the expected maximal force, whereas in case of specimens of MW-c-0.67 series the unloading, after first 7 cycles, was realized up to the 2/3 of the expected maximal force. The expected maximal compressive force was determined by test of the reference specimen MW-d.

For all tested specimens were determined the envelope curve as it has presented in Fig. 2(b). It is visible the no-linear elastic behaviour of the tested masonry wallettes. During the tests were recorded the value of the compressive stresses and in-plane deformations in both orthogonal directions by the set of LVDT’s transducers, shown also in Fig. 2(a). Very carefully was recorded the moment of the first cracks appearance.

The main results of the tests as well as computational analyses are shown below in Table 1. The values of the initial modulus of elasticity $E_{0,i}$ were determined from the stress-strains curve relationship in the interval from $\sigma =$ 0 to $\sigma =$ 0.33${\sigma }_u$, whereas the $E_{0,cal}$ using Eq. (1). The values of $E_{cr,i}$ correspond to the value of the elastic modulus, determined for the first cracks.

Fig. 2The shape and overall dimensions of: a) masonry wall specimens tested by Galman [15] with visible the localization of the set of LVDT’s transducer, b) typical stress-strain relationship for masonry subjected to cyclic loading of specimens of series MW-c with the construction of the envelope curve

a)

b)

Analysis of the comparison of the initial values of modulus of elasticity $E_{0,i}$ determined in cyclic tests with obtained in one-cycle test shows generally a little higher values representing cyclic loading. Furthermore the values of modulus of elasticity for the state of the first visible cracks $E_{cr,i}$ by the reason of the not-elastic behaviour and micro cracking were not exceeds 75 % of the initial values (obtained from the tests) what corresponded with the acceptance of the damage factor $D_c$ in Eq. (2) at the level of 0.25. This same value of damage factor (for plastic and micro cracking of the material) is recommended in [17]. Whereas, the calculation of the Young’s modulus $E_{0,cal}$, specified in Eurocode 6 [1] (Eq. (1)) seems to be too high in relation to the experimental data (see the values shown in last column in Table 1). Therefore, in situation when in the calculations we have to rely on standard values and requirements, it is necessary to reduce the value of the elastic modulus by at least 60 % in relation to calculated from Eq. (1).

3.1. Theoretical considerations

According to the most of European national masonry standards, including Eurocode 6 [1] in masonry structure analysis the value of shear modulus can be taken as:

where $E_0$ is an initial secant modulus of elasticity.

In case of in-plane shearing of masonry wall specimens, the value of the shear modulus $G_i$ may be determine based on the value of shear stresses ${\tau }_i$ and shear strains ${\mathrm{\Theta }}_i$ using the formula:

This relationship is particularly useful in situations where the displacement of the edge of the wall under the shear load is not directly measured, only the deformation parameters are measured in the middle area of the test element, e.g. in one cycle in-plane shear tests or diagonal compression tests according to ASTM E519/E519M-15 [20] standard.

In the case of testing the elements of walls subjected to cyclic shear, the shear modulus is usually determined based on characteristic parameters, among others, such as elastic stiffness $K_e$, maximum horizontal force $H_{max}$, geometrical data of tested specimens and taking into account the bending and shear deformations, can be calculating as:

where $K_e$ is the elastic stiffness of the wall; $h$, $l$, $t$ are the height, length and width of the wall specimen; $A$ is the floor area of the wall ($A=l·t$), $E$ is the modulus of elasticity, $\delta$ is the coefficient for the boundary conditions ($\delta =$ 3 for cantilever and $\delta =$ 12 for walls restraint on both sides) and $\kappa$ is the shear stress coefficient (for rectangular cross section $\kappa =$ 1.2).

Of course, masonry is typical anisotropic body and the value of shear modulus is changing with accordance with the state of loading and deformation. Therefore, taking in calculations values of shear modulus $G$ according to Eq. (3) is equal with omission of plastic and damage deformation of masonry. In real structures and loading, including seismic and dynamic effects, the values of shear modulus, especially for higher levels of internal stresses, is significantly lower than obtained from Eq. (3). Therefore, such an overvalued determination of shear modulus is increasingly criticized in the literature on the subject [4-9] and [18]. It leads to serious underestimations of structure deformations, which is the basis for the analysis of limit states and safety of structures, e.g. calculated in accordance with Eurocode 8 [2] for seismic areas. Also, the American FEMA P440A [19] regulations also require consideration of material stiffness degradation when calculating buildings for seismic influences.

Therefore, in calculation and analysis of shear (stiffening) walls the following, based on the Continuum Damage Mechanics, reduced values of shear modulus is proposed:

where $D_s$ is the damage variable characterised the variation of the shear modulus and describing the kinetics of the plasticity and damage process of the masonry from the range (0 ≤ $D_s$ ≤ 1) and $G_0$ is the initial value of the modulus of elasticity for the elastic behaviour of the material.

3.2. Experimental results and its discussion

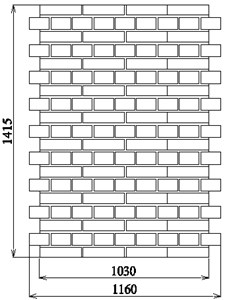
Then problem of shear stiffness degradation is analysed by author for many years, especially from the point of view of calculating masonry buildings in the areas of paraseismic influences caused by mining activity. There were carried out many tests of wall type specimens subjected to vertical or horizontal shearing with and without vertical precompression. All these tests concerned shearing in one cycle. Among others, series masonry wallettes made of clay solid bricks strength class “25” ($f_b=$ 25 MPa) and cement-lime mortar class M5 (1:1:6) were subjected to vertical shearing without and with six levels of precompression (${\sigma }_c$ stresses). The shape and overall dimensions of tested wallettes is shown in Fig. 3(a). Thickness of the specimens was 0.25 m and English bond was used. All wall specimens were tested in one cycle up to the failure. During all tests were recorded the vertical shear force and in-plane deformations using set of LVDT’s transducers used in compression tests and shown in Fig. 2(a).

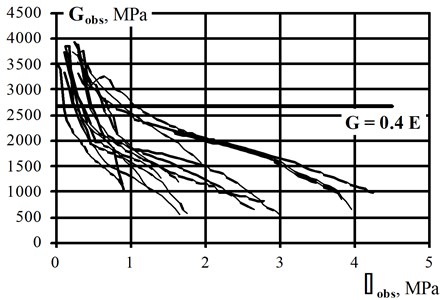
Fig. 3The shape and overall dimensions of: a) masonry wall specimens in author’s tests, b) relationship Gobs–τobs for tested wallettes

a)

b)

The main results as level of vertical compressive stresses ${\sigma }_{c,i}$, shear stresses ${\tau }_{i,obs}$ noted for the first visible diagonal cracks and corresponding to them values of the shear strains ${\mathrm{\Theta }}_{i,obs}$ are shown in Table 2.

In the next two columns are presented values of shear modulus determined based on test data using Eq. (4) and based on standard recommendation, Eq. (3), respectively. The last column covers the comparison of these two determined values. It is easy to see the values of shear modulus received from tests $G_{i,obs}$ are roughly half of the values calculated based on Eurocode 6 [1] recommendations. This results in 0.2$E$. This means that the value of the damage factor $D_s$, should be taken in this case as $D_c=$ 0.5. The relationship $G_{obs}-{\tau }_{obs}$ for tested wallettes, presented the non-linear decrease of the shear modulus in relation to the vertical shearing stresses in graphical form with recommended in Eurocode 6 [1] value $G=$ 0.4$E$ is shown in Fig. 3(b).

Interesting cyclic shear tests of masonry wall specimens made of clay solid bricks with the dimensions of 290×140×65 mm corresponded to the old Austrian standard format and cement-lime mortar class M5 were carried out by Zimmermann et al. [8]. The shape of the wallettes of tested series was built with English bond and dimensions of 2390×2990×290 mm (length×height×thickness). In complementary material tests were determined the compressive strength of the masonry $f_k=$ 6.52 MPa and modulus of elasticity $E_{test}=$ 1522 MPa.

During the tests the load level of the normal force was determined with 1.30 MPa (20 % of the maximal value) to avoid the occurrence of a pure friction or compressive failure. The horizontal load was applied displacement-controlled, each with three similar displacement amplitudes in one dimension and a subsequent increase ±0.25 mm etc. until failure of the wall.

The results of the computational analysis are shown in Table 3. The tested values of the shear modulus $G$ were calculated using Eq. (5) based on the elastic stiffness $K_e$ taking into account the bending and shear deformations of tested wallettes (calculated for 90 % of the maximal horizontal forces $H_{max}$ from the hysteresis envelope. In fourth column are presented the values of shear modulus calculated using standard recommendation (Eq. (3)).

The comparison of the values of shear modulus received from tests $G_{i,obs}$ were not exceeding 22 % of the calculated using Eq. (3). Thus, it could be assumed $G_{i,obs}\approx$ 0.22$E_{test}$ – quite similar than in case of vertical shearing in one cycle. It could be taken that the value of the damage factor $D_s$, should be taken in this case as $D_s=$ 0.5. A similar results were obtained by the other researchers, among other in [4] are presented the test results of determination of the shear modulus in relation to the Young’s modulus. The values of G modulus vary from 6 % to 25 % of the elastic modulus $E$ and never have values as high as 0.4 $E_0$, as specified and recommended in Eurocode 6 [1].