Abstract
This paper presents the dynamic response of the Indian Railway track. Two track models are considered for the dynamic response in terms of vertical displacement and acceleration at different wheel speeds, keeping the moving point load at constant magnitude. The rail is treated as a beam either on viscoelastic foundation or on the discrete elastic support system. The governing equation is implemented in finite element analysis using ANSYS 14.0. For the validation of result from system equation are compared with those available in published literature and the maximum deviation for displacement at the midpoint of rail is found to be within 5 %. Different wheel speed generates variation in displacement and acceleration of the rail track. The study can be viewed as the foundation for the comparison of FEA based simulation of rail track to specify its dynamic response useful to provide better safety and comfort to commuters.
1. Introduction
The dynamic analysis of the railway track is a critical area of interest for many investigators around the world. The modern trend towards higher speed in the railway has further intensified the research to accurately predict the vibration behavior of railway track. The design of rail and foundation has become a significant factor in stress analysis, passenger comfort and noise reduction. The track is often modeled as an infinite beam on Winkler foundation which consist closely spaced linear spring. Timoshenko [1] was one of the first to model the dynamic behavior of railway track. Fryba [2] presented vibration of solid and structure under moving load that includes most of the published result before 1999. Wang et al. [3]provided a review for beam and plates on elastic foundation which focused on designing the foundation system.
The foundation models are developed by researchers like Pasternak [4], Vlasovand Leentiev [5], Kerr [6], Reissner [7]. Mallick et al. [8] compared results in terms of the normalized bending moment and deflection for beam on elastic foundation by considering foundation as one and two parameter foundation models. The results showed that difference in the modeling of the foundation either as one or two parameter model is insignificant on bending moment and deflection. Uzzal et al. [9] compared the dynamic response of Euler-Bernoulli beam subjected to moving load and moving mass supported by two parameters Pasternak foundation. Thambiratnam and Zhuge [10] developed finite element method for dynamic analysis of beam on elastic foundation subjected to moving point load. They proved that beam of span length 10 m can accurately approximate as the ideal beam of infinite length. Hu D. et al. [11] presented the convergence of the Galerkin method for the dynamic response of a Euler- Bernoulli beam resting on a non-linear viscoelastic foundation subjected to moving load. Abdelghany et al. [12] presented the dynamic response of the non-uniform beam subjected to moving load and resting on non-linear viscoelastic foundation.
This paper focuses on the comparison for track acceleration of two well known models in this area: Beam on viscoelastic foundation and discrete elastic support representing the system model. The track acceleration indicates the intensity by which the track responds to dynamic loading. It is an important factor to analyze ballast loosening, ballast flying and ballast pad stability to obtain uniform track elasticity (Agarwal S. K., Professor Bridges, Indian Railways Institute of Civil Engineering, Pune, unpublished data). To address this aspect of research, finite element method with ANSYS as a tool is used for 2-D modeling of beam. In the present work, both the beam and foundation are assumed to be homogenous and isotropic. For the validation of present models, a track and foundation are designed as per the literature. The maximum deviation for displacement at the midpoint of rail is found well within the acceptable range. This is also supported by the results reported in Thambiratnam and Zhuge [10] for dynamic amplification in deflection that deviated up to 5 %. The technique of modeling is extended to model beam on viscoelastic foundation and beam on discrete elastic support. Single wheel is considered as moving point load and for different wheel speed track vertical deflection and acceleration are calculated and compared. Analysis is carried out for typical data of Indian Railways obtained from different literatures of Croft [13], Srivastava et al. [14] and (Agarwal S. K., Professor Bridges, Indian Railways Institute of Civil Engineering, Pune, unpublished data).
2. Finite element model
2.1. Beam on viscoelastic foundation (BOVF)
The beam on viscoelastic foundation is considered. A spring-damper element COMBIN40 is attached to a 15 m long beam (Beam element: BEAM188) in vertical direction (-axis). The ground nodes of foundation are constrained for all degree of freedom. Beam element is 0.1 m long and spring damper is attached at extremities of the beam elements.
The governing equation of motion for a Euler- Bernoulli beam on viscoelastic foundation can be given by Eq. (1), (Mallik et al. [8]):
In case of moving load:
where, is the Young’s modulus of elasticity of the beam material, is the second moment of area of the beam cross-section about its neutral axis, is the mass per unit length of beam, is the coefficient of viscous damping per unit length, is spring constant of foundation per unit length, is the applied moving point load per unit length, is the space coordinate measured along the length of beam, is the time in seconds, is the constant speed of point load and is the Dirac delta function.
Fig. 1Beam elements on viscoelastic foundation
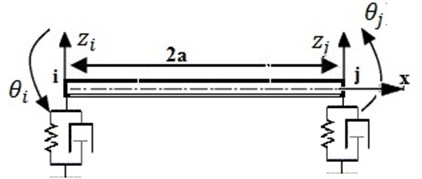
Consider an element of length 2, having a uniform cross section as shown in Fig. 2. To generalize the equation of motion for the track finite element model may be written as:
where , and are the global mass, damping and stiffness matrix for the finite element model and is the vector of vertical displacement of the model. is a vector of force and moments acting on the nodes of the model. The mass matrixand stiffness matrixof the beam elements is determined using Euler-Bernoulli beam theory as described by Petyt [15].
2.2. Beam on discrete elastic support
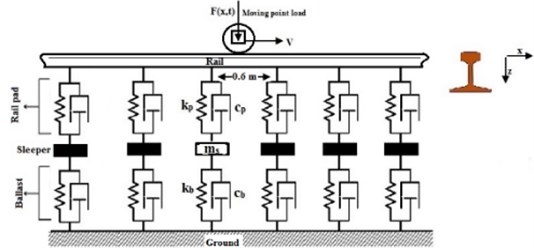
Fig. 2 shows a 2D model of beam on discrete elastic support. Rail is modeled as Euler-Bernoulli beam supported by 6 mm rail pad which act as massless spring and damper between rail and sleeper. Sleeper is considered as concentrated mass and ballast as spring- damper of 0.2 m depth. The sub-grade layer is neglected. The track is modeled as beam element (BEAM 188) of length 0.6 m. The mass and stiffness matrix of rail is same as the above. The mass, stiffness and damping matrix for a rail pad element is described by Croft [13].
Each rail pad element connects a rail node and sleeper node. The degree of freedom of the model allows vertical displacement and rotation of half sleeper mass and vertical displacement of ballast layer.
The ballast is modeled as massless spring and damper. Any damping in the rotational degree of freedom due to the ballast layer is neglected. The ground nodes of ballast layer are constrained for any displacement and rotation. The mass, stiffness and damping matrix for the foundation is described by Croft [13].
Fig. 2Beam on discrete elastic support
3. Results and discussion
To validate the model, a simply supported beam on non-linear viscoelastic foundation subjected to a concentrated load moving with 36 km/h, is analyzed as per the properties of the UIC60 rail. The results are compared with the existing numerical solution of Ding et al. [11],where the dynamic response of the beam on non-linear viscoelastic foundation was obtained via the Galerkin method.
Results for the vertical displacement of rail at midpoint are computed and compared in Table 1. It can be seen that the present result, obtained through the ANSYS 14.0, compared quite well with the result of Ding et al. [11] and thereby confirm the validity of the model. The maximum deviation in displacement at the midpoint of rail is found 5 %, which can be acceptable; especially as per the result reported in Thambiratnam and Zhuge [10] for dynamic amplification in deflection by using finite element method deviated up to 5 % during validation of the numerical procedure. The technique of modeling beam on non-linear viscoelastic foundation is extended to model beam on viscoelastic foundation and beam on discrete elastic support.
Table 1Vertical displacement at the midpoint of rail
Time (sec) | Vertical displacement (mm) | ||
Ding et al. [11] | Present result | Comparison (in %) | |
0.1 to 0.5 | 0 | 0 | 0 |
0.6 | –0.033 | –0.0315 | 4.54 |
0.7 | –0.0583 | –0.0562 | 3.60 |
0.8 | 0.125 | 0.125 | 0 |
0.9 | 0.3833 | 0.4025 | 5.0 |
1.0 | 0.25 | 0.26 | 4.0 |
1.1 | 0.1033 | 0.108 | 4.54 |
1.2 | –0.0166 | –0.0158 | 4.81 |
1.3 | –0.02 | –0.019 | 5.0 |
1.4 to 1.8 | 0 | 0 | 0 |
3.1. Comparison of models for vertical displacement at different speed
Computational analyses are carried out for the models described in section 2.1 and 2.2. The dynamic response in term of vertical displacement and acceleration is obtained with respect to time and the position of the beam. The input parameters are as per the Indian railways standard. Fig. 3 shows the vertical displacement response at the midpoint for beam on viscoelastic foundation and discrete elastic support at different velocities. The maximum deflection for beam on viscoelastic foundation is 0.25 mm for 50 and 250 km/h. However, the maximum deflection for beam on discrete elastic support is 0.6 mm for 50 and 250 km/h. The maximum deflection is higher in case of beam on discrete elastic support, which is attributed to the fact that elastic support is provided at every 0.6 m from left end of beam whereas for viscoeleatic foundation, elastic support is at every 0.1 m.
The result also shows that the influence of the travelling speed is quite insignificant on the vertical displacement of relatively larger foundation stiffness. The negative value of deflection signifies the downward deflection with the moving load. A small amount of positive deflection occurs in distance away from the load. The positive deflection is about 0.05, 0.07 and 0.1 mm for discrete elastic support shows that with increase in speed, upward deflection and vibration of track increases, which may lead to dynamic instability for the moving train and deterioration of the track life. Such variation in upward deflection at different speed is not seen for beam on viscoelastic foundation.
Fig. 3Comparison of deflection for beam on viscoelastic foundation and discrete elastic support: a) 50 km/h, b) 250 km/h
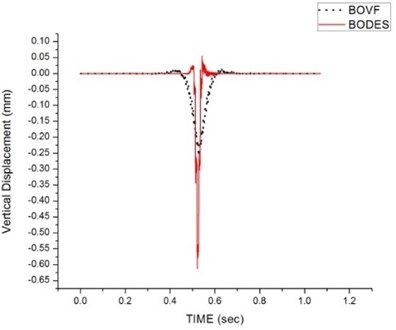
a)
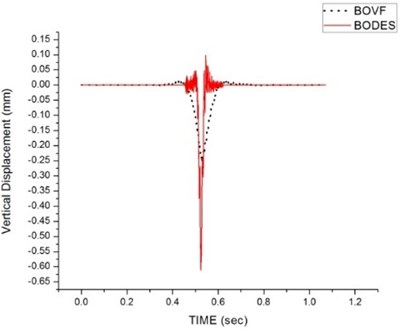
b)
3.2. Comparison of both models for vertical acceleration at different speed
The variation of vertical acceleration at the midpoint of the track for both models at different speeds is shown in Fig. 4 and 5. Similar to deflection response, the maximum acceleration is calculated for the midpoint of the beam. The maximum acceleration for beam on viscoelastic foundation is –102.92, –210.2 and –310 m/s2 at 50,150 and 250 km/h respectively. The maximum acceleration for the discrete elastic support is –38.5, –223.2 and –504.5 m/s2 at 50, 150 and 250 m/s2 respectively.
The acceleration for discrete elastic support is higher than the beam on viscoelastic foundation. For beam on viscoelastic foundation, acceleration away from the midpoint can be neglected, but for discrete elastic support it accelerates significantly. The stability of the foundation depends upon the acceleration of the track and for given Indian railways standard, it is not suitable to go beyond 250 km/h.
The change in acceleration may attenuate the rail pad and ballast stiffness and also the dynamic stability of the rail. High speed trains can be achieved by proper maintenance of track, by changing the level of ballast foundation and by introducing new higher stiffness rail pad.
Fig. 4Acceleration for beam on viscoelastic foundation at: a) 50 and 150 km/h, b) 150 and 250 km/h
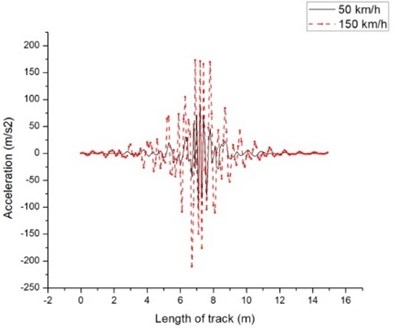
a)
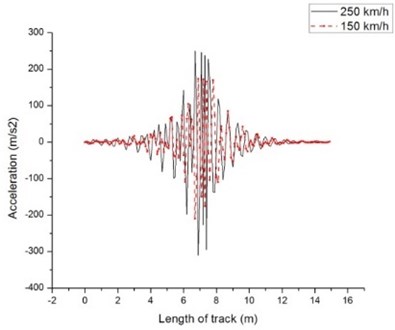
b)
Fig. 5Acceleration of beam on discrete elastic support at: a) 50 and 150 km/h, b) 150 and 250 km/h
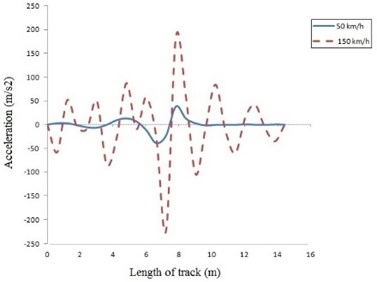
a)
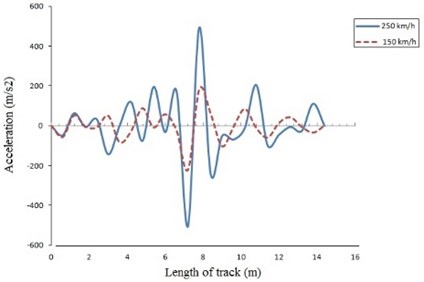
b)
4. Conclusions
The paper presents the result in term of vertical displacement and acceleration for an Euler-Bernoulli beam on viscoelastic foundation and discrete elastic support of Indian railway track at constant load for different speed.
The result indicates maximum deviation for midpoint displacement of rail to lie within 5 % of values reported in Thambiratnam and Zhuge [10].
For the chosen R-60 profile of Indian rail indicates that, the change in wheel speed doesn’t modify the vertical deflection but drastic change in acceleration occurs.
The discrete elastic support condition indicates higher value for deflection and acceleration than that with viscoelastic foundation.
References
-
Timoshenko S. Method of analysis of statistical and dynamical stresses in rail. Proceedings of Second International Congress for Applied Mechanics, Zurich, 1926, p. 407-418.
-
Fryba L. Vibration of Solids and Structures under Moving Loads. Thomas Telford, London, 1999, p. 206-231.
-
Wang Y. H., Tham L. G., Cheung Y. K. Beams and plates on elastic foundations: a review. Progress in Structural Engineering and Materials, Vol. 7, Issue 4, 2005, p. 174-182.
-
Pasternak P. L. Fundamentals of a new method of analyzing structures on an elastic foundation by means of two foundation moduli. Gosudarstvennoe Izdatelstro Liberaturi po Stroitelstvui Arkhiteckture Moscow, 1954, (in Russian).
-
Vlazov V. Z., Leontiev U. N. Beams, Plates and Shells on Elastic Foundations. Israel Program for Scientific Translations, Jerusalem, 1966, (in Russian).
-
Kerr A. D. Elastic and viscoelastic foundation models. Journal of Applied Mechanics, Vol. 31, Issue 3, 1964, p. 491-498.
-
Reissner E. A note on deflection of plates on a viscoelastic foundation. Journal of Applied Mechanics, Vol. 80, 1958, p. 144-145.
-
Mallik A. K., Chandra S., Singh A. B. Steady-state response of an elastically supported infinite beam to a moving load. Journal of Sound and Vibration, Vol. 291, Issues 3-5, 2006, p. 1148-1169.
-
Uzzal Rajib Ul Alam, Bhat Rama B., Ahmed Waiz Dynamic response of a beam subjected to moving load and moving mass supported by Pasternak foundation. Shock and Vibration, Vol. 19, Issue 2, 2012, p. 205-220.
-
Thambiratnam D., Zhuge Y. Dynamic analysis of beams on an elastic foundation subjected to moving loads. Journal of Sound and Vibration, Vol. 198, Issue 2, 1996, p. 149-169.
-
Hu D., Li Qun C., Shao Pu Y. Convergence of Galerkin truncation for dynamic response of finite beams on nonlinear foundations under a moving load. Journal of Sound and Vibration, Vol. 331, Issue 10, 2012, p. 2426-2442.
-
Abdelghany S. M., Ewis K. M., Mahmoud A. A., Nassar M. M. Dynamic response of non-uniform beam subjected to moving load and resting on nonlinear viscoelastic foundation. Beni–Suef University Journal of Basic and Applied Science, Vol. 4, Issue 3, 2015, p. 192-199.
-
Croft B. E. The Development of Rail-head Acoustic Roughness. Ph.D. Thesis, Institute of Sound and Vibration Research, University of Southampton, 2009, p. 50-86.
-
Srivastava J. P., Sarkar P. K., Ranjan V. Contact stress analysis in wheel-rail by Hertzian method and finite element method. Journal of Institution of Engineers, India: Series C, Vol. 95, Issue 4, 2014, p. 319-325.
-
Petyt M. Introduction to Finite Element Vibration Analysis. Cambridge University Press, Cambridge, 1990, p. 53-140.
-
Chen Y. H., Huang Y. H. Dynamic stiffness of infinite Timoshenko beam on viscoelastic foundation in moving co-ordinate. International Journal for Numerical Methods in Engineering, Vol. 48, Issue 1, 2000, p. 1-18.
-
Mishra D., Qian Y., Huang H., Tutumluer E. An integrated approach to dynamic analysis of railroad track transitions behavior. Transportation Geotechnics, Vol. 1, Issue 4, 2014, p. 188-200.
