Abstract
Basing on the dynamic response characteristics of the periodic structure under a moving harmonic load in frequency domain and the superposition principle, the dynamic response of track structure under variable speeds moving harmonic load is investigated. Firstly, the track is simplified as an Euler beam model periodically supported by continuous discrete point, the dynamic differential equation of vertical vibration for the track structure is formulated. Secondly, for convenience of analysis, the analytical expression for the amplitude-frequency response of any point on the track structure under the moving harmonic load is derived in frequency domain. Based on the theory of the infinite periodic structure, the dynamic responses of the track structure under the variable speed moving harmonic load are analyzed theoretically. Finally, the influences of velocity and acceleration on the dynamic response of track structure are numerically analyzed in detail. The research results indicate that the amplitude-frequency response peaks of the track under moving harmonic load with variable and constant speeds occur near the excitation frequency. The displacement response of the track increases slightly with increase of the acceleration, and the variation trend of dynamic response is basically similar. The vibration displacement response of the rail can be effectively improved by increasing the initial velocity of the moving harmonic load, while the peak value of amplitude-frequency response remained constant.
1. Introduction
With the rapid development of urban rail transit in our country, the vibration and noise caused by train operation are becoming more and more prominent. Many experts and scholars at home and abroad have paid close attention to it [1, 2]. The urban rail transit area is shorter in our country currently, than the train is always in the state of variable speed in the transmission line. Li X. and Zhang Z. J. et al. [3] used the vibration theory to study the vertical dynamic response analysis model of Euler-Bernoulli beam under the arbitrary moving load columns. However, the model only considered the vibration response under uniform moving load, and couldn’t solve the variable moving load. Sun W. and Zhou J. et al. [4] modeled the rail as Euler beam on a two-parameter elastic foundation, and suggested that the random vibration response of the vertical coupled system of track was studied by the Green function method. But all the research cases always remained under the uniform moving load. The literature review shows that existing investigations are mainly confined to the uniform condition of urban rail trains, and to the research on the Variable moving load is seldom addressed.
To make up these deficiencies, a vertical interaction model of a periodic track resting on infinite spans of elastically-supported girders is established in this paper to investigate the dynamic characteristics of track structures under a variable speed moving load. Firstly, the related problems of solving the track vibration response under mobile loads are transformed to solve a system of first-order equation of 4 variables in frequency domain by using the Fourier transform [5], is based on the fully consideration of the characteristics of the track structure itself. The analytical expression for the dynamic response of any point on the track structure under a variable speed moving harmonic load is efficiently derived consequently in the periodical scope. Secondly, the periodic analytical expressions for the dynamic response of arbitrary point on the track structures under a variable speed moving harmonic load is investigated, which is on the basis of the characteristics of the periodic structure’s response in frequency domain, and concretely analyze the influence of acceleration and initial velocity of the moving load on dynamic response of track structure.
2. Formulation of the model
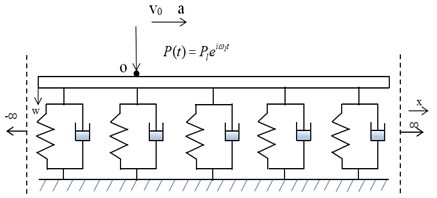
The rails is modelled as a single Euler-Bernoulli beam periodically supported by continuous discrete point with spacing , as shown in Fig. 1. The is vertical deflection, is harmonic concentrated force, and are initial velocity and acceleration respectively. The point 0 corresponds to one of the supports and the indicated as the initial position.
Fig. 1Model of the beam periodically supported by continuous discrete point
The governing equations of motion for the track under moving harmonic excitation is given by:
where an are the bending stiffness and the mass per unit length of the rails, respectively. is the Dirac function. represents the fulcrum reaction of the sleeper caused by the moving of the load on the rail.
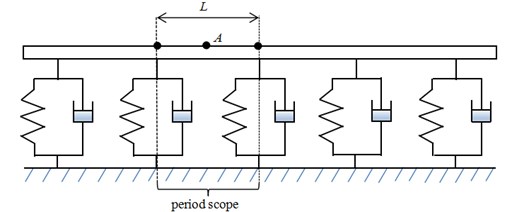
Based on the theory of the infinite periodic track structure, the solution of the track dynamic response problem is converted to one period, and the coordinate [0 ] is taken as the periodic scope [6], as shown in Fig. 2.
Fig. 2Periodic track structure and period scope
The local coordinate system is established in a periodic scope , the differential equation of rail vibration between two adjacent supports () is written as:
where is the initial velocity in each periodic scope, and sign “-“ denotes the variable in local coordinate system.
Using Fourier transformation for Eq. (2), the differential equation of the rail vibration in the frequency domain is given by:
where is the displacement response of vertical vibration of rail in frequency domain.
Therefore, the general solution of Eq. (3) is expressed by:
where , .
The four unknowns in Eq. (4) are written in the following vector form:
The function and its partial derivatives and are continuous at the point 0, but the transverse shear force in the beam, , experiences the sudden change of ; this is equal to the elastic reaction of the support at this location, as shown in Fig. 3.
Fig. 3The infinite periodically supported beam
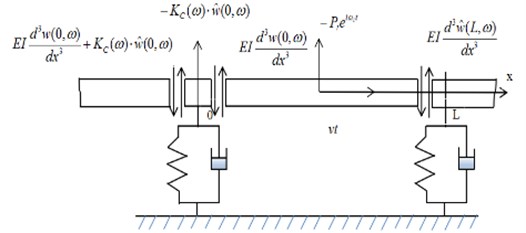
According to the theory of periodic structure and the boundary conditions of one periodic scope of beam, one can obtain [7]:
where is the composite stiffness, and , and are the stiffness and damping of the support layer, respectively.
Simultaneous Eq. (4) and Eqs. (6), the matrix equation is written as:
where is an unknown constant vector. and are 4×4 matrices and 4×1 vectors, respectively.
According to the characteristics of dynamic response of infinite periodic structure, the solutions of any one point outside the beam periodic scope can be expressed as [8]:
By sampling the angular frequency by cycle, it is obtained that the analytic solution of the dynamic response of arbitrary point on the track structure under variable moving harmonic loads. The displacements in the space-frequency domain are transformed to the time domain numerically using the discrete inverse Fourier transform on this basis.
3. Dynamic response analysis of track structures
In this section, the dynamic responses of the track structure under a variable speed moving harmonic load are illustrated numerically [9], including the amplitude-frequency response, the time-domain response, parameters effects on the dynamic behaviors.
Firstly, two cases of uniform moving load and variable speeds moving load are considered respectively, i.e. 20 km/h, 1 m/s2. The point A are used to locate the mid-span point of track structure (see Fig. 2). The dynamic responses of the system are presented numerically at the pick-up point A as the excitation frequency response 30 Hz, shown in Fig. 4. Fig. 4(a) presents the displacement amplitude-frequency response of track structure system and Fig. 4(b) is presents the dynamic responses of track structure system in the time domain. There exists response peak in the vicinity of excitation frequency. On the whole, the dynamic response of track structure under variable moving harmonic load is higher than dynamic response of track structure under uniform moving harmonic load.
Fig. 4The vibration displacement comparison of point A
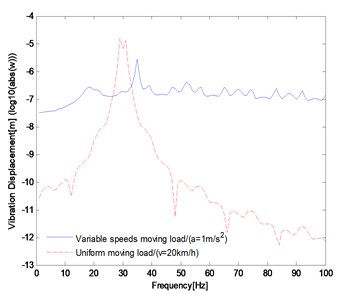
a)
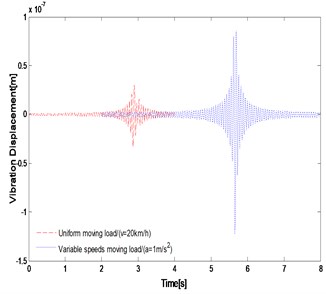
b)
The effects of acceleration on the dynamic response of track structure at point A are presented when the excitation frequency 30 Hz, shown in Fig. 5. Four value of acceleration, i.e. 1 m/s2, 3 m/s2, 6 m/s2, 9 m/s2 are considered. It can be seen from Fig. 5 that the variation trend of dynamic response is similar under the condition of four different acceleration, but the displacement amplitude-frequency response of the track increases slightly with the elevation of moving acceleration. Fig. 5(a) presents that the amplitude-frequency response peak occurs in the vicinity of the excitation frequency, and the amplitude-frequency response decreases rapidly at the area away from the excitation frequency. The amplitude-frequency response peak will move towards higher frequency with the increase of acceleration. In Fig. 5(b) shows the time history of the response of track structure. The response peak of the track occurs in sequence at the moment of the load passes through point A at different acceleration.
Fig. 5Influence of the acceleration on the dynamic response of track structure
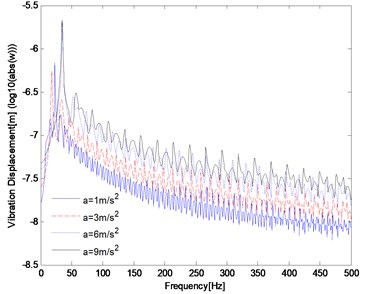
a)
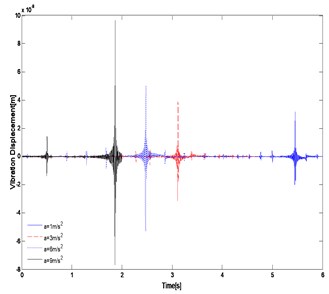
b)
The effects of initial velocity on the dynamic response of track structure are analyzed numerically when the excitation frequency 30 Hz, shown in Fig. 6. Four value of initial velocity, i.e. 0 km/h, 10 km/h, 20 km/h, 30 km/h are considered. According to Fig. 6, the variation trend of dynamic response is similar under the condition of four different initial velocity, and the displacement amplitude-frequency response of the track increases effectively with increasing the initial velocity of the moving harmonic load.
Fig. 6Influence of the initial velocity on the dynamic response of track structure
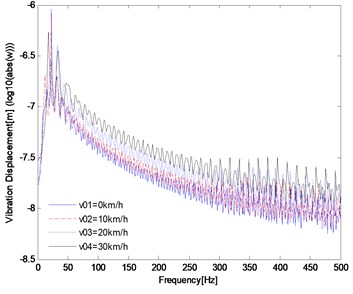
a)
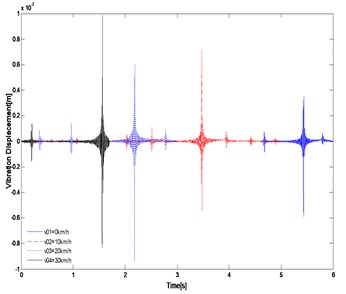
b)
From Fig. 6(a), the amplitude-frequency response peak occurs in the vicinity of the excitation frequency, and the amplitude-frequency response decreases rapidly at the area away from the excitation frequency. In Fig. 6(b), the time history of the response of track structure is presented. The response peak of the track occurs in sequence at the moment of the load passes through point A at different initial velocity.
Comparing Fig. 5 and Fig. 6, it is found that the influence of the acceleration of moving load on the dynamic response of track structure is much more significant than that the initial velocity of moving load in resonance frequency domain. The current model has only addressed the case of a harmonic moving load on the infinite periodic tracks with single track. To understand the dynamics of a train running on such a track and the effect on vibration in the far field, a model of a train should be coupled to the track. This model is currently under development by the authors.
4. Conclusions
This paper presents the study on dynamic response of track structure under variable moving harmonic load. The track is divided into a number of periodic beam units by the span length of two adjacent sleepers. Using the theory of infinite periodic structure, the dynamic responses of the track structure are solved analytically in the frequency domain. Influences of the initial velocity and the acceleration on the dynamic response of track structure are investigated numerically. Through the analysis and comparison of the dynamic responses of track structures under different parameters, the following conclusions can be drawn:
1) For two cases of uniform moving load and accelerated moving load, the amplitude-frequency response peaks occur both in the vicinity of excitation frequency. On the whole, the dynamic response of track structure under variable moving harmonic load is higher than the dynamic response of track structure under uniform moving harmonic load.
2) Acceleration has a significant influence on the dynamic response of the track structure, and the response peak of system moves towards higher frequency when the value of acceleration increases. The vibration displacement responses increase slightly with the elevation of moving acceleration.
3) Initial velocity has a significant influence on the dynamic response of the track structure, and the displacement amplitude-frequency response of system the increases effectively when the initial velocity of the moving harmonic load increases.
References
-
Connolly D. P., Kouroussis G., Laghrouche O. Benchmarking railway vibrations – track, vehicle, ground and building effects. Construction and Building Materials, Vol. 92, 2015, p. 64-81.
-
Zhang D., Li X. Analysis and application of vertical dynamic response of simply supported beam bridge under moving harmonic load series. Chinese Journal of Applied Mechanics, Vol. 31, Issue 1, 2014, p. 144-149.
-
Li X., Zhang Z., Liu Q. Vertical dynamic response analysis of a simply supported beam bridge under successive moving loads. Journal of Vibration and Shock, Vol. 31, Issue 20, 2012, p. 137-142.
-
Sun W., Zhou J., Thompson D. Vertical random vibration analysis of vehicle-track coupled system using Green's function method. Vehicle System Dynamics, Vol. 52, Issue 3, 2014, p. 362-389.
-
Xia H., Zhang N., Roeck G. D. Dynamic analysis of high speed railway bridge under articulated trains. Computers and Structures, Vol. 81, Issue 26, 2003, p. 2467-2478.
-
Hussein M. F. M., Hunt H. E. M. A numerical model for calculating vibration due to a harmonic moving load on a floating-slab track with discontinuous slabs in an underground railway tunnel. Journal of Sound and Vibration, Vol. 321, Issues 1-2, 2009, p. 363-374.
-
Belotserkovskiy P. M. On the oscillations of infinite periodic beams subjected to a moving concentrated force. Journal of Sound and Vibration, Vol. 193, Issue 3, 1996, p. 705-712.
-
Sheng X., Zhong T., Li Y. Vibration and sound radiation of slab high-speed railway tracks subject to a moving harmonic load. Journal of Sound and Vibration, Vol. 395, 2017, p. 160-186.
-
Shi L., Cai Y., Wang P. A theoretical investigation on influences of slab tracks on vertical dynamic responses of railway viaducts. Journal of Sound and Vibration, Vol. 374, 2016, p. 138-154.
