Abstract
In the fields of aerospace, precision machinery and energy, there are variable-diameter tubes for many key components. Abrasive flow polishing technology is an effective precision polishing technology for finishing the workpiece with an internal cavity structure. This technology can improve the quality of part finishing, reduce stress concentration, and reduce the surface roughness of the workpiece, and ultimately can improve the performance of the workpiece. In this paper, variable-aperture tube is taken as the research object, and the characteristics of abrasive flow in the multi-physics coupling field are studied by numerical simulation, and the collision removal effect between the abrasive particle and the wall surface is analyzed. We also discussed the control law of the abrasive grain flow processing quality and provided theoretical guidance for abrasive grain flow polishing of this type of part.
1. Introduction
Abrasive flow polishing technology uses a viscoelastic soft abrasive medium loaded with abrasive particles to reciprocate through the part’s processing surface under pressure to effect finishing [1]. The abrasive flow moves back and forth with the piston in the media cylinder, abrasive grains in the abrasive flow can be regarded as numerous grinding tools, the surface and corners of parts are machined by abrasive grains with hard and sharp edges [2]. In the fluid, particles and particles, particles and fluids, particles and walls will collide and rebound, so that any part of the flow through the abrasive particles will be polished. For some parts with special channels, the advantage of abrasive flow polishing technology is particularly prominent [3, 4].
Since the variable-aperture tube has different internal diameters, the state of the medium in the variable-aperture tube will change to achieve the purpose of throttling or connecting tubes or lenses of different sizes. Variable-aperture tubes are widely used in aerospace, medical, food, engineering and optical lenses, so people have higher and higher requirements for their machining accuracy [5, 6]. However, due to changes in its internal pore size, it is difficult to polish its inner surface. Therefore, it is suitable to polish the inner surface with the abrasive flow polishing technology [7, 8].
2. Selection of the processing parameters of solid-liquid two phase abrasive flow
The numerical simulation of the process of abrasive flow processing requires relevant settings for the multiphase flow model and the turbulence model. The multiphase flow model in this paper uses a dense discrete phase model combining a discrete phase model and a hybrid model. The turbulence model uses the standard - model, where the empirical constants are , , and , respectively. The collision of the particles was simulated using a direct simulation Monte Carlo method and using user-defined functions (UDF) to program, the collision model was embedded into the numerical simulation of solid-liquid two-phase abrasive flow. When the solid-liquid two-phase abrasive flow is simulated, the physical properties of the liquid phase fluid and the solid phase abrasive particles should be set. The fluid density was set to 1260 kg/m3, the fluid thermal conductivity was set to 0.15 w/(m·K), the SiC abrasive particle density was set to 3100 kg/m3, and the SiC abrasive thermal conductivity coefficient was set to 1200.15 w/(m·K). The velocity inlet was selected as the inlet boundary condition, the initial turbulent intensity was 5 %, and the initial abrasive concentration was 12 %. The free outlet is selected as the outlet boundary condition to ensure that the fluid state is turbulent. The wall boundary conditions adopt the no-slip wall boundary conditions, and the near wall areas adopt the standard wall equations for processing. Since the calculation process is an unsteady process, the selected time step should be small enough to ensure the accuracy of the particle collision sampling. This paper selects the time step of particle is 1×10-6 s, the time step of fluid is 1×10-4 s, and the calculation time is 1 s.
3. Numerical simulation analysis of precision polishing variable-aperture tube with abrasive flow
3.1. Three dimensional modeling and mesh generation of variable-aperture tube
The internal aperture of the third-order variable-aperture tube is symmetrically changed, that is, the internal aperture first becomes smaller and then becomes larger, and the apertures on both sides are symmetrical with respect to the middle section. The third-order variable-aperture tube model is shown in Fig. 1.
Fig. 1Three-dimensional model of variable-aperture tube

The established three-dimensional model is imported into the meshing software for meshing, and the mesh type is selected with a good quality hexahedral mesh. The divided mesh model is shown in Fig. 2.
Fig. 2Mesh model of variable-aperture tube

The quality of the mesh directly determines the accuracy of the calculation results, so the better the quality of the mesh, the higher the accuracy of the calculation results. If the mesh is too rough, it may cause the calculation result to not converge, resulting in a large error in the calculation. Therefore, after the meshing is completed, the quality of the mesh needs to be checked. Fig. 3 shows the results of checking the mesh quality. It can be seen from Fig. 3 that the mesh quality of the variable-aperture tube mesh model is greater than 0.5, which has reached the corresponding calculation requirements and can be used for numerical analysis of abrasive grain flow polishing.
Fig. 3Measured results of variable-aperture tube mesh quality

3.2. Numerical simulation analysis of variable aperture tube
The entrance velocity of the abrasive flow was set to 30 m/s, the mass flow was set to 0.02 kg/s, and the direction of gravity is the same as the direction of the velocity. The numerical simulation uses the large hole end face of the variable-aperture tube as the entrance, and the small hole end face of the variable-aperture tube as the exit, and the variable-aperture tubes under the two conditions of considering particle collision and not considering particle collision were simulated. After the numerical calculation, dynamic pressure distribution maps of variable-aperture tubes under two conditions can be obtained. As shown in Figs. 4 and 5.
Fig. 4Dynamic pressure cloud diagram of variable-aperture tube without considering particle collision

Fig. 5Dynamic pressure cloud diagram of variable-aperture tube with considering particle collision

The dynamic pressure is the kinetic energy per unit volume of the fluid. Its size is equal to the difference between the total pressure and the static pressure, reflecting the movement of the fluid in the flow channel, which is basically consistent with the velocity distribution. From Fig. 4 and Fig. 5, it can be seen that the trend of dynamic pressure of the abrasive flow under these two conditions is basically the same. However, consider the dynamic pressure of the abrasive flow under the particle collision conditions to be greater. The dynamic pressure at the first-order and second-order aperture changes of the variable-aperture tube significantly increases, and the dynamic pressure at the second-order pinhole reaches a maximum value. This is because the smaller the diameter of the pores makes the movement of the fluid at the smaller pore diameters more violent, thereby increasing the dynamic pressure. The dynamic pressure at the second and third-order aperture changes becomes smaller, and as the fluid continues to approach the outlet, the dynamic pressure near the wall increases. This is because the flow from the second-order to the third-order of the abrasive flow is a process that flows from a small aperture to a large aperture. At the initial end, the abrasive flow moves along the small hole to the big hole, and there is less movement on the wall. With the continuous forward movement, the abrasive flow will be filled with the whole flow path. Therefore, the dynamic pressure in the middle area is getting smaller and smaller, and the dynamic pressure near the wall area is getting larger and larger. Through analysis, it can be seen that for this type of variable-aperture tube, the first-order and second-order processing results are better, and the third-order processing results are worse. Therefore, a bi-directional processing method can be used to ensure the uniformity of the polishing process. In order to more intuitively embody the changing law of dynamic pressure, the centerline of the section is selected as the reference line, and the value of dynamic pressure on this line is made into a line graph of the change trend shown in Fig. 6.
Fig. 6Changing trend of dynamic pressure value of variable-aperture tube
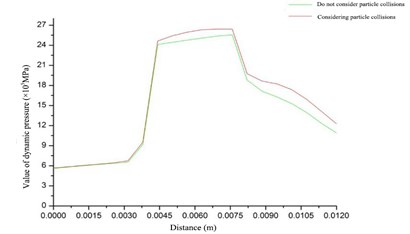
As can be seen from Fig. 6, the two-fold lines almost coincided in the initial stage. This shows that the collisions between the particles at the first-order are small, and the impact on the fluid is also small. After the change of the pore size, the collision of the particles at the change of the pore diameter is more severe and has a greater impact on the fluid. Therefore, the dynamic pressure value under considering the particle collision condition is large. After the second-order and third-order aperture changes, since the aperture of the variable-aperture tube is changed by the radial large aperture of the small hole, the fluid movement gradually spreads from the middle to both sides. Therefore, the dynamic pressure value in the middle part gradually decreases, and the dynamic pressure value under consideration of the particle collision condition decreases more slowly.
Fig. 7Particle distribution cloud diagram of variable aperture tube without considering particle collision

Fig. 8Particle distribution cloud diagram of variable aperture tube with considering particle collision

Fig. 7 and Fig. 8 are particle distribution cloud diagrams of variable-aperture tubes. It can be seen from the figures that the distribution of particles in the variable-aperture tube is relatively uniform without considering the particle collision conditions, and only the particles at the change of the pore diameter have a slight distribution change. This is due to the fact that without considering the collision of particles, the particles are regarded as part of the fluid and as the fluid continues to move, all the effects of the particles are accomplished by the fluids acting on them. Therefore, under this condition, the motion of the particles is approximately the same as the motion of the fluid. In the area of change between the second-order and third-order, the fluid gradually spreads from the middle to the wall surface, and at the same time, it can be seen that the particle distribution also shows a tendency to spread from the middle to the two sides. While considering the collision of particles, the distribution of particles has changed significantly. In the area of change between the first and second stages, the distribution of particles is significantly increased, and at the middle hole, the grains become more. This is due to the consideration of particle collisions, random collisions occur between the particles and the particles, although the fluid still has a leading effect on the particles, but the collision between the particles and the particles will make the particles more irregular movement, especially in the small aperture, its violent movement the degree goes far beyond the large aperture. Therefore, the mass flow at the small aperture is larger than the mass flow at the large aperture. In the area of change between the second-order and third-order, similar to the case where the particle collision is not considered, the particle motion also gradually spreads from the middle to both sides, so the particle distribution also has the same tendency.
4. Conclusions
1) In the process of precise polishing of the abrasive flow in the multi-physics coupling field, the solid-phase abrasive particles are driven by the liquid-phase fluid to perform disorderly and irregular movements on the surface to be processed of the workpiece, and the movement of fluids and abrasive particles has a direct effect on the abrasive flow polishing effect. The abrasive particles slide with the fluid on the surface to be processed of the workpiece to micro-cut the material on the workpiece surface so as to achieve the effect of removing the surface material of the workpiece to be processed, thereby completing the polishing of the workpiece surface by the abrasive flow.
2) Through the numerical simulation of the third-order variable-aperture tube under both considering abrasive grain collisions and ignoring abrasive grain collisions conditions, it was found that the impact of abrasive particles has a certain influence on the polishing quality of the abrasive flow. In the case of considering the collision of abrasive particles, the dynamic pressure is slightly larger than that without considering the collision of the abrasive particles. In the abrasive flow polishing process, the collision between the abrasive particles can effectively improve the dynamic pressure of the abrasive flow, thereby improving the polishing effect on the inner surface of the third-order variable-aperture tube. Therefore, during the abrasive flow polishing process, the collision between the abrasive particles will have a positive influence on the processing effect of the abrasive flow polishing, which is beneficial to the polishing of the wall surface.
References
-
Li Junye, Meng Wenqing, Dong Kun, Zhang Xinning, Zhao Weihong Study of effect of impacting direction on abrasive nanometric cutting process with molecular dynamics. Nanoscale Research Letters, Vol. 13, 2018, p. 11.
-
Marzban Mohammad Ali, Hemmati Seyed Jalal Modeling of abrasive flow rotary machining process by artificial neural network. International Journal of Advanced Manufacturing Technology, Vol. 89, Issues 1-4, 2017, p. 125-132.
-
Jani Kenda, Franci Pušavec, Janez Kopac Modeling and energy efficiency of abrasive flow machining on tooling industry case study. Procedia CIRP, Vol. 13, 2014, p. 13-18.
-
Sun Shufeng, Ji Shiming, Tan Dapeng Research on turbulence regulation of low viscosity liquid-solid two-phase abrasive flow and finishing technology of structural surfaces. China Mechanical Engineering, Vol. 22, Issue 19, 2011, p. 2349-2353.
-
Li Junye, Wei Lili, Zhang Ximing, et al. Quality analysis of T-tube with solid-liquid two-phase abrasive flow polished. Journal of Measurements in Engineering, Vol. 5, Issue 2, 2017, p. 77-86.
-
Li Junye, Su Ningning, Zhao Weihong, Yin Yanlu, Hu Jinglei Study on the polishing of curved pipe parts by solid liquid two phase abrasive flow. Journal of Measurements in Engineering, Vol. 5, Issue 2, 2017, p. 59-67.
-
Spratling M. Nanofinishing of freeform surfaces using abrasive flow finishing process. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, Vol. 6, Issue 9, 2015, p. 206-207.
-
Li Junye, Meng Wenqing, Zang Xiang, et al. Numerical simulation analysis of large eddy simulation for T-tube based on solid-liquid two-phase abrasive flow. Vibroengineering Procedia, Vol. 14, 2017, p. 313-317.
About this article
The authors would like to thank the National Natural Science Foundation of China No. NSFC51206011, Jilin Province Science and Technology Development Program of Jilin Province No. 20160101270JC and No. 20170204064GX.
