Abstract
Damage detection and localization in civil engineering constructions using dynamic analysis has become an important topic in recent years. This paper presents a methodology based on non-destructive detection, localization and quantification of multiple damages in simple and continuous beams, and a more complex structure, namely two-dimensional frame structure. The proposed methodology makes used of Firefly Algorithm and Genetic Algorithm as optimization tools and the Coordinate Modal Assurance Criterion as an objective function. The results show that the proposed combination of Coordinate Modal Assurance Criterion and Firefly Algorithm or Genetic Algorithm can be easily used to identify multiple local structural damages in complex structures. However, the convergence rate becomes slower for the case of multiple damages compared to the case of single damage. The effect of noise on the algorithm is further investigated. It is found that the proposed technique is able to detect the damage location and its severity with high accuracy in the presence of noise, although the convergence rate became slower than in the case when no noise is present. It is also found that the convergence rate of Firefly Algorithm is much faster than that of Genetic Algorithm.
1. Introduction
Damage detection in civil engineering constructions using dynamic system parameters has become an important research topic. The cost of repair is obviously less than that required to reconstruct the whole structure. Visual inspection technique has a limited capability to detect damage, especially when damage lies inside the structure and is not visible. During the last decades, the use of the dynamic system parameters such as natural frequencies, damping ratio and mode shapes to detect damage qualitatively and quantitatively has been studied intensively. Besides, it is very important to ensure the integrity and stability of structures, to prevent extensive failure, and to reduce the cost of maintenance [1]. The reason of this popularity is the ease of measuring modal parameters on real structures. The natural frequencies and the mode shapes are directly related to the stiffness of the structure. Therefore, a drop in natural frequencies or a change in mode shapes will indicate a loss of the stiffness. As cracks create new surfaces, the damping ratio will increase when damage progresses in the structure.
Genetic Algorithm is a very attractive technique compared to conventional optimization methods because it does not require a search within the entire space of solution [2]. Likewise, Firefly Algorithm is one of the most powerful algorithms for optimization [3, 4]. The change in modal parameters e.g. natural frequencies, damping ratios and mode shapes can easily indicate the presence of damage and its severity. Applications of this concept have been reported in the literature, such as damage detection in composite materials [5] and in off-shore structures [6]. For a better localization of damage, other dynamic parameters have been proposed, namely power spectral densities [7] and curvature of mode shapes [8], which showed more sensitivity to damage than the mode shapes themselves. Application of this method to bridges has been reported in the literature by many researchers, e.g. Williams and Salawu [9], Sikorsky and Stubbs [10] and Farrar and Jauregai [11].
The above technique is called the “response-based approach” since the response data are directly related to damage. This approach is therefore fast and inexpensive. Another method known as “the model-based approach” [12-16] has been proposed to detect damage based on updating certain parameters to get perfect agreement between the experimental measured modal parameters and an initial finite element model. The updated parameters can be used afterwards to evaluate damage and identify its location. The drawback of such a method lies in the requirement of reducing the numerical model or extending the measured modal parameters. This is due to the fact that not all degrees of freedom in the numerical model can be measured because of practical reasons. This second approach is more expensive and time consuming than the former approach. However, the latter approach is more suitable for complex structures. For an introductory textbook for the updating techniques and their applications, the reader may refer to Friswell and Mottershead [17]. Adams and Coppendale [18] have presented methods of identification of defects in a qualitative relation to the location of defect and its importance. Damage approach prediction in beam and plate structures with initiated damage was presented in the literature [19]. The results provided the basis for the development of diagnostics algorithms. Khatir et al. [20, 21] have used MAC, COMAC and LFCER for detecting and locating damage in beam-like structures using vibration analysis. Amrane and Sidoroff [22] dealt with the evaluation of the residual modal energy in glass/epoxy unidirectional fibrous composite beam at a desired state using vibration analysis, while Khatir et al. [23] worked on the damage detection and localization based on vibration analysis using Bat algorithm on thin plates using vibration analysis.
In this paper, the multiple structural damage identification and localization problem is addressed by means of Firefly Algorithm (FA) and Genetic Algorithm (GA). The objective function used in the optimization process is based on vibration data using Co-ordinate Modal Assurance Criterion (COMAC). Various numerical examples are performed on simply supported beam and a two-dimensional frame structure. The paper is organized as follows. In Section 2, the optimization technique based on FA and GA, and the objective function based on COMAC are described. Applications of the proposed technique to a damaged beam and a 2-D frame structure are presented in Section 3. The effect of noise on the efficiency of the algorithm is investigated in Section 4. Finally, some concluding remarks are given in Section 5.
2. Description of optimization method
2.1. Genetic algorithm for damage detection
Genetic Algorithm, originally developed by Holland [24], combines algorithms to solve optimization problems using the principles of evolution. It demonstrated excellent operations in combinatorial optimization that have a finite solution. Potential solutions are sought through a population of individuals, i.e. candidate solutions, which evolve towards an optimum solution. Each individual has a set of properties, known as chromosomes, which can be mutated and altered during the optimization process. The initial population usually generates random individuals and the evolution progressed in an iterative way. After each iteration, a new population, called a generation, is created. During the process of GA, a fitness function, which has the value of objective function in an optimization problem, is evaluated in each iteration. The individuals that best fit the objective function are selected and used in the next generation after recombination and possibly random mutation and reproduction. The iteration process continues until either a satisfactory minimization of the objective function is obtained or the maximum defined number of iterations is reached.
In our study, the individuals are the sets of damage parameters and the chromosomes are the damage parameters themselves, i.e. the stiffness of the structure at different locations, and the fitness or objective function to be minimized is based on COMAC as it will be presented later in section 2.3. All numerical studies presented in this paper are implementing in MATLAB. In applying GA, the following steps are programmed:
Step 1: Creating a random initial population of individuals and elements’ stiffness as chromosomes.
Step 2: Creating a sequence of new populations at each iteration using the current population. To achieve this step, the algorithm does the following:
• Compute the score of each individual by calculating its fitness.
• Convert the fitness scores into a more usable range of values.
• Select individuals or members, called parents, based on their scores.
• Select individuals or members, called elite, which have lower score, and pass them to the next generation.
• Produce children from the parents by making random changes to a single parent (mutation) or combining a pair of parents (crossover).
• Form the next generation using the current population and its children.
Step 3: Stop the algorithm when the stopping criteria is met. In our implementation, the maximum number of iteration is set equal to 100.
2.2. Firefly Algorithm for damage detection
The Firefly Algorithms focus on the variation of light intensity and formulation of the attractiveness. To simplify this concept, we can always consider that the attractiveness of a firefly is determined by its brightness, which in turn is associated with the encoded objective function based on frequencies, e.g. comparing the measured and calculated frequencies as in our case, where the brightness of a firefly at a particular location x can be chosen as . However, as the attractiveness is relative, it should be seen in the eyes of the beholder or judged by the other fireflies [25]. Thus, it will vary with the distance between firefly and firefly .
Some of the flashing characteristics of fireflies can be realized in order to develop firefly-inspired algorithms. For the description of Firefly Algorithm (FA) that is used herein, three rules will be considered:
1) All fireflies are unisex so that one firefly will be attracted to other fireflies regardless of their sex;
2) Attractiveness is proportional to their brightness, thus for any two flashing fireflies, the less bright one will move towards the brighter one. The attractiveness is proportional to the brightness and they both decrease as their distance increases. If there is no brighter one than a particular firefly, it will move randomly;
3) The brightness of a firefly is affected or determined by the landscape of the objective function. For a maximization problem, the brightness can simply be proportional to the value of the objective function.
In addition, light intensity decreases with the distance from its source, and light is also absorbed in the media, so the attractiveness variation with the degree of absorption must be allowed. In the simplest form, the light intensity varies according to the inverse square law:
where is the intensity at the source. For a given medium with a fixed light absorption coefficient , the light intensity vary with the distance r, i.e.:
where is the original light intensity.
As a firefly’s attractiveness is proportional to the light intensity seen by adjacent fireflies, the attractiveness of a firefly can be defined by:
where is the attractiveness at 0.
In our study the parameters used are 1, [0, 1], 1 and 1.5. In addition, if the scales vary significantly in different dimensions such as −105 to 105 in one dimension while, say, −0.001 to 0.01 along the other, it is a good idea to replace by ,where the scaling parameters ( 1,..., ) in the dimension should be determined by the actual scales of the problem of interest.
2.3. Objective function
The objective function used in this study is based on the Co-ordinate Modal Assurance Criterion (COMAC) [26]. The COMAC is calculated over a set of mode pairs, which can be numerical/numerical, numerical/experimental or experimental/experimental set of data. It is an extension of the classical well-known Modal Assurance Criterion (MAC), which is widely used by researchers for modal correlation. The main intension of the COMAC is to identify which measured degrees of freedom contribute negatively to a low value in the MAC matrix. In other words, it localizes the mismatch in the structure between two mode pairs of modal data. In damage detection application, these mode pairs are for those of damaged and intact structures. The two modal vector COMAC uses the eigenvectors for each degree of freedom () in the structure and is given by [26]:
where and are the healthy and damaged mode shapes, respectively, is the indices for (measured) degree of freedom number, is the indices for mode shape number and is the total number of modes considered in the calculation. The COMAC values vary between 0 and 1 and for a good correlation it should be close to 1. Therefore, in damage detection application, COMAC should be far below 1 at a damaged location in the structure. Based on COMAC, the objective function to be minimized is defined as follows:
In order to determine the eigenvectors required to calculate COMAC for intact and damaged structures, finite element simulations were carried out. Classical Euler-Bernoulli beam element was programmed in MATALAB and eigenvalue problem is solving to determine the modal data. The equation of motion can be obtained for free vibrations, in the absence of damping, and is written as:
where [] and [] are the mass and stiffness matrices, respectively and is the displacement vector. By solving Eq. (6) for the eigenvalues and eigenvectors, the data required for COMAC are obtained. In applying GA to beam structures, hard constrains of the stiffness by specifying maximum and minimum values are considered. The maximum value is the stiffness of the intact beam, while the minimum value is set equal to zero.
3. Results and discussion
In this section, we investigate the accuracy of the proposed optimization techniques by considering two numerical examples, namely simply supported beam and a two-dimensional frame structure. Different damage scenarios, with single and multiple damages are introduced to these structures in order to produce simulated modal parameters. Damage was simulated by reducing the stiffness of selected elements at different positions. FA and GA are then applied to these damage scenarios and the locations of damage and its severities are identified. The effect of noise is further investigated by introducing noisy data to the modal parameters and reapplying our techniques.
3.1. Simply supported beam
For a simply supported beam shown in Fig. 1, the following geometrical and mechanical properties are used: length 6 m, cross-section area 0.09 m2, density 2500 kg/m3 and stiffness 20.25 ×106 N.m2 [27]. A finite element model is constructed using 10 beam elements as shown in Fig. 1. The intact beam is modelled using a constant stiffness, , for all elements, while the damaged beam is modeled by reducing of some specific elements. The beam is macroscopically considered homogeneous. Three different damage scenarios, D1, D2 and D3, were considered using different locations of damage and a reduction in stiffness in the damaged elements:
Scenario D1: A single damage at element 2 – reduction in stiffness of 50 %.
Scenario D2: A single damage at element 8 – reduction in stiffness of 30 %.
Scenario D3: A multiple damage at element 2 and 8 – reduction in stiffness of 50 % in element 2 and 30 % in element 8.
Fig. 1Simply-supported beam structure discretized in 10 elements

Fig. 2The iteration process of objective function based on FA and GA - damage scenario D1
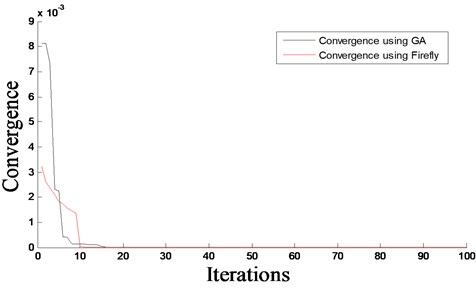
The predicted damage locations and severities, as well as the convergence rates, for both proposed algorithms, are shown in Figs. 2-7 for all considered damage scenarios D1 to D3, respectively. From Figs. 2-7, it can be seen that good results are obtained using FA and GA, which predict accurately the location of damage and its severity with a small amount of error. Furthermore, the damage detection algorithm based on FA provides mush faster convergence rate that that based on GA. It can be also observed that damage scenario D2 has a slightly faster convergence that scenario D1. This can be due to the fact that in D2 the damage is more towards the middle of the beam that in case of D1. For the multiple damage scenario, D3, this study shows that FA and GA together with COMAC can effectively identify multiple damages in beams. It can also be observed that the rate of convergence of damage scenarios D1 and D2 is faster than that of D3. This is because D1 and D2 have only a single damage, whereas D3 has two damages at two different locations.
Fig. 3Evolutionary process of damage index – damage scenario D1
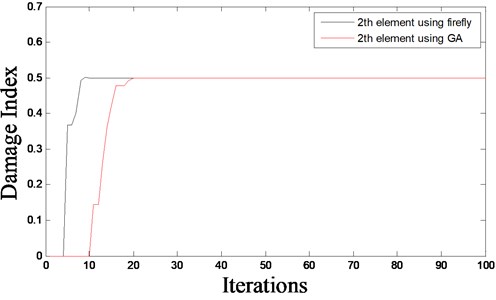
Fig. 4The iteration process of objective function based on FA and GA – damage scenario D2
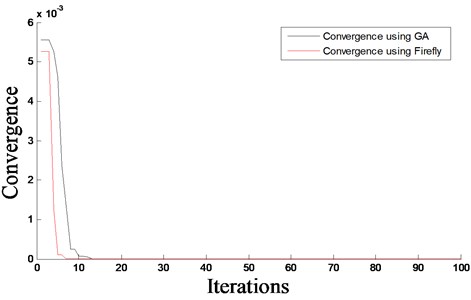
Fig. 5Evolutionary process of damage index – damage scenario D2
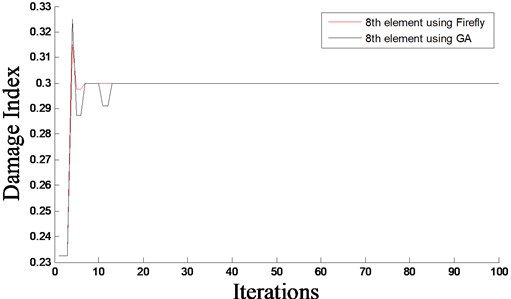
Fig. 6The iteration process of objective function based on FA and GA – damage scenario D3
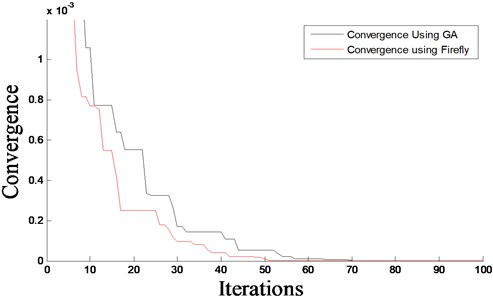
Fig. 7Evolutionary process of damage index – damage scenario D3
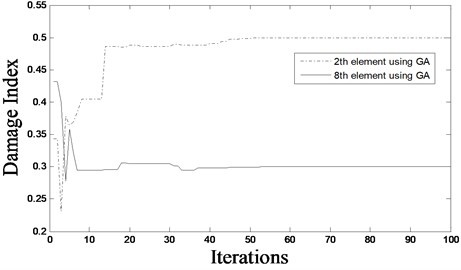
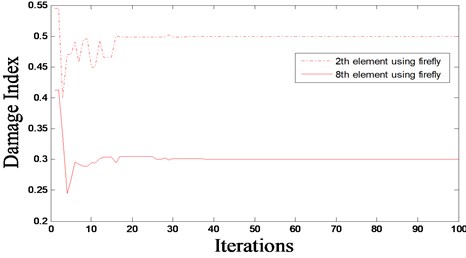
3.2. Damage of a two-dimensional frame structure
We consider now a more complex structure, namely a two-dimensional frame structure as shown in Fig. 8. It consists of 17 beam elements, 10 nodes and 30 DOFs. This structural system is used to evaluate the ability of the proposed methodology to detect damage in a more complex structure. As it has been seen in the previous numerical example, FA has a better performance than GA and provides faster convergence, therefore only FA is used in this analysis. The material constants of the frame structure are: elastic-modulus 20×109 N/m2 and density 7780 kg/m3. In this study, a multiple damage scenario, D4, is considered using different locations and severities of damage:
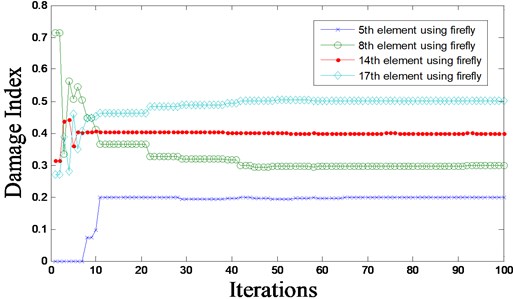
Scenario D4: Multiple damages – reduction in stiffness of 20 %, 30 %, 40 % and 50 % in elements 5, 8, 14 and 17, respectively.
The predicted damage locations and severities, as well as the convergence rates, are shown in Figs. 9 and 10 for damage scenario D4 using FA. From Figs. 9 and 10, it can be seen that good identification of damage locations and severities are obtained. This demonstrates the accurate prediction of our approach in case of multiple damages in complex structures. Regarding convergence rate, it can be seen that the damage scenario D4 shows slower convergence rate when compared to scenarios D1 and D2. Again, this sounds as logic results since scenario D4 contains four locations of damages with different severities, whereas D1 and D2 contain one location. Thus, the more damage locations in the structure, the slower the convergence rate and the more CPU time required.
Fig. 8A two-dimensional frame structure discretized in 17 beam elements
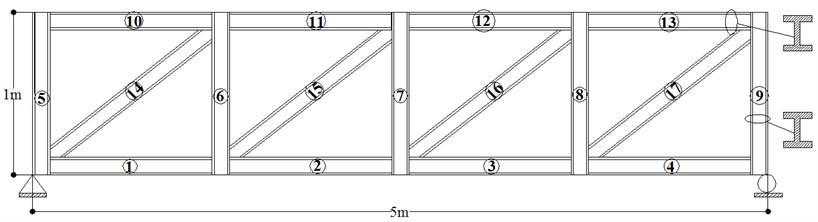
Fig. 9The iteration process of objective function based on FA – damage scenario D4
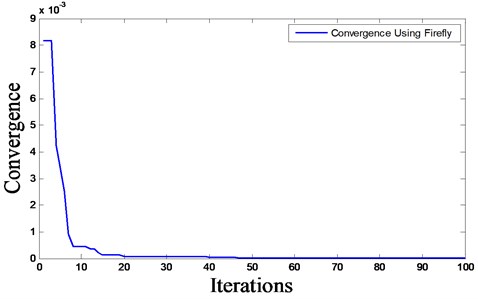
Fig. 10Evolutionary process of damage index – damage scenario D4
It is worth mentioning that the objective function used in FA, Eq. (4), depends on the boundary conditions. This is because COMAC is a function of modal vectors, which depend on boundary conditions. If the boundary conditions are changed to clamped-clamped or free-free, a different modal vector will be produced for not only the intact girder, but for also the damaged one. By using these two modal vectors in Eq. (4) and applying FA, damage can be detected in a way similar to that for the simply supported case.
4. Effect of noise
In order to investigate the effect of noise on our damage detection technique, White Gaussian noise was considered on complete and incomplete (first ten modes) modal data for damage scenario D4. The th noisy response , is simulated by [28]:
where is the noise level and is a random number in the interval [−1; 1]. Noise level of 10 % is introduced to the reference data of D4. The convergence of the results is shown in Fig. 11. Comparing Fig. 9 with Fig. 11, it can be seen that the convergence rate becomes slower by increasing the noise level. Thus, the higher the noise level, the slower the convergence rate and the more CPU time required for convergence. The results are also summarized in Table 1 for comparison purposes between the estimated damage severities in scenario D4 with and without noise.
Table 1Comparison between real damage and estimated damage for D4 with noise
Element | Real damage (%) | Estimated damage with noise |
5 | 20 | 19.56 |
8 | 30 | 29.69 |
14 | 40 | 39.63 |
17 | 50 | 50.06 |
False alarms: 1, 4, 7, 10, 12 and 16 | 0 | 0.09, 0.02, 0.06, 0.009, 0.03 and 0.06 |
Fig. 11Convergence of damage scenario D4 with 10 % noise level
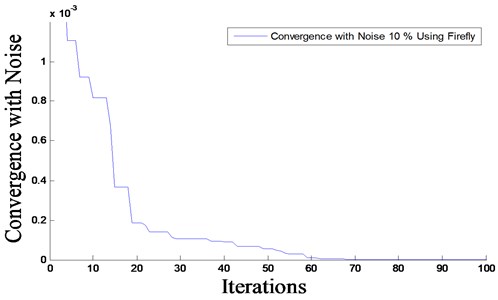
From the results, we can observe that, when the noise is included in the problem of fault detection, our approach based on Firefly algorithm can detect damage with high accuracy.
5. Conclusions
In this paper, an optimization approach has been developed and used for vibration analysis of beam-like and complex structures to detect and locate multiple and single damage. The approach is based on using Firefly Algorithm and Genetic Algorithm as optimization techniques and the Co-ordinate Modal Assurance Criterion as objective function. A theoretical study using simulated data for a simply-supported and a two-dimensional frame structure has been conducted. The study showed that the Firefly Algorithm and Genetic Algorithm were effective to identify the locations and severities of multiple damages in complex structures. However, Firefly Algorithm provided faster convergence rate than Genetic Algorithm. It was also concluded that the convergence rate depended on the location of damage and the number of damages in a structure. The more damages in the structure, the slower the convergence rate. When the noise effect was taken into consideration, it was shown that our approach was able to detect the damage locations with high accuracy. However, the convergence rate became slower in case of high noise level compared to the case when no noise was present.
References
-
Yan Y. J., Cheng L., Wu Z. Y., Yam L. H. Development in vibration-based structural damage detection technique. Mechanical Systems and Signal Processing, Vol. 21, Issue 5, 2007, p. 2198-2221.
-
Khatir S., Belaidi I., Roger S., Benaissa B., AitSaada A. Genetic algorithm based objective functions comparative study for damage detection and localization in beam structures. Journal of Physics: Conference Series, Vol. 628, Issue 1, 2015, p. 012035.
-
Yang X. S. Firefly algorithm, Levy flights and global optimization. Research and Development in Intelligent Systems XXVI, Springer, London, 2010, p. 209-218.
-
Yang X. S. Firefly algorithms for multimodal optimization. International Symposium on Stochastic Algorithms, Springer, Berlin Heidelberg, 2009, p. 169-178.
-
Adams R. D., Walton D., Flitcroft J. E., Short D. Vibration testing as a nondestructive test tool for composite materials. American Society for Testing and Materials, Composite Reliability, Philadelphia, Vol. 580, 1975, p. 159-175.
-
Vandiver J. K. Detection of structural failure on fixed platforms by measurements of dynamic response. Proceedings of the Seventh Annual offshore technology Conference, 1975, p. 243-252.
-
Nauerz A., Fritzen C. P. Error localization using power spectral densities. The 21th International Seminar on Modal Analysis, Noise and Vibration Engineering, 1996, p. 973-982.
-
Pandey A. K., Biswas M., Samman M. M. Damage detection from changes in curvature mode shapes. Journal of Sound and Vibration Vol. 145, 1991, p. 312-332.
-
Williams C., Salawu O. S. Concepts of Condition Assessment of Bridges Using Vibration Testing and Analysis. Bridge Assessment Management and Design, Elsevier, London, 1994.
-
Sikorsky C., Stubbs N. Structural Damage Assessment Using Advanced Signal Processing Procedures. Improving Bridge Management Using NDT and Quality Management. Sheffeld University Press, 1997, p. 399-408.
-
Farrar C., Jauregai D. Damage Detection Algorithms Applied to Experimental and Numerical Modal Data. Technical Report, LA-1304-MS, National Laboratory, Los Alamos, 1996, p. 1-40.
-
Abdel Wahab M. M., De Roeck G., Peeters B. the application of FE model updating to damaged concrete beams. Proceedings of the International Conference on Identification in Engineering Systems, University of Wales Swansea U.K., 1999, p. 29-31.
-
Ahmadian H., Mottershed J. E., Friswell M. I. Damage detection from substructure modes. The 21th International Seminar on Modal Analysis (ISMA 21), Noise and Vibration Engineering, 1996, p. 983-991.
-
Nake H. G., Cempel C. Fault detection and localization in structures: a discussion. Mechanical Systems and Signal Processing, 1991, p. 345-359.
-
Hajela P., Soeiro F. J. Structural damage detection based on static and modal analysis. AIAA Journal Vol. 28, 1990, p. 1110-1115.
-
Zimmerman D. C., Kaouk M. Structural damage detection using a minimum rank updating theory. Journal of Vibration and Acoustics, Vol. 116, 1994, p. 222-231.
-
Friswell M. I., Mottershead J. E. Finite Element Model Updating in Structural Dynamics. KLUWER Academic Publisher, Dordrecht, The Netherlands, 1995.
-
Adams R. D., Coppendale J. Measurement of the elastic module of structural adhesives by a resonant bar technique. Journal of Mechanical Engineering Science, Vol. 18, Issue 3, 1976, p. 93-100.
-
Petkevicius K., Volkovas V. Monitoring and identification of structural damages. Mechanics, Vol. 17, Issue 3, 2011, p. 246-250.
-
Khatir S., Serra R., Belaidi I. Détection et localisation de défauts dans des structures poutres par analyse vibratoire. 4ième Congrès Algérien de Mécanique, 2013.
-
Samir Khatir, Idir Belaidi, Roger Serra, Magd Abdel Wahab, Tawfiq Khatir Damage detection and localization in composite beam structures based on vibration analysis. Journal of Mechanika, Vol. 21, Issue 6, 2015.
-
Amrane M. N., Sidoroff F. Residual modal energy evaluating of fatigue damaged composite structure. Mechanics, Vol. 17, Issue 1, 2011, p. 45-49.
-
Khatir A., Tehami M., Khatir S., Abdel Wahab M. Damage detection and localization on thin plates using vibration analysis. Proceeding of 23rd International Congress on Sound and Vibration (ICSV23). International Institute of Acoustics and Vibration, 2016.
-
Holland J. H. Adaptation in natural and artificial systems. 2nd Edition. The University of Michigan Press, Ann Arbor, MI, MIT Press, Boston, MA, 1992.
-
Yang Xin-She Firefly Algorithm, Levy Flights and Global Optimization. Research and Development in Intelligent Systems XXVI, Springer, London, 2010. p. 209-218.
-
Ewins D. J. Modal Testing: Theory and Practice. Research Studies Press Ltd., 2000.
-
Wahab M. A., De Roeck G. Damage detection in bridges using modal curvatures: application to a real damage scenario. Journal of Sound and Vibration, Vol. 226, Issue 2, 1999, p. 217-235.
-
Gerist S., Naseralavi S. S., Salajegheh E. Basis pursuit based genetic algorithm for damage identification. International Journal of Optimization in Civil Engineering, Vol. 2, Issue 2, 2012, p. 301-331.
