Abstract
This paper presents a new damage detection and localization technique based on the changes in vibration parameters using BAT and Particle Swarm Optimization algorithm. The finite element method is used to apply damage at specific element(s) of the considered beams. The damage is represented by a reduction in Young’s modulus and the identification of damage is formulated as an optimization problem using objective function based on Modal Scale Factor and changes in natural frequencies. A procedure for detecting and locating damage of beam-like structures based on BAT algorithm is used. This approach presents a method that can be used to detect the single and multiple-damage positions and the rate of damage in structural elements with high accuracy after the first iteration. The results obtained using BAT algorithm are compared to those obtained using Particle Swarm Optimization Algorithm. By taking noise into account in the damage detection and localization problem, it is shown that our approach based on BAT algorithm can detect the damage locations with high accuracy.
1. Introduction
In the recent years, a structural damage detection became a field that has attracted a lot of interest in the scientific community. There have been many studies and researches intending to find a reliable method to detect and localize damage in structural elements using optimization methods. BAT algorithm (BA) is recently introduced as an effective optimization algorithm and was successfully applied to several problems [1-6]. Identifying structural damage using measured vibration data is an inverse approach in mathematics. The normal damage detection methods produce an objective function, which is defined in terms of the differences between the data identified by modal vibration tests and those calculated from analytical or finite element model [7, 8]. The genetic algorithm (GA) was used to produce a sufficiently optimized amplitude characteristic filter to extract damage information from the strain energy mode shapes [9]. A finite element (FE) model was used to generate training data set with the known location. The changes in the natural frequencies together with FE models to find the damage was proposed [10]. An uncertainty approach for damage detection was suggested [11]. The coordinate modal assurance criterion (COMAC), which makes use of the numerical and experimental vibration modes, was used to determine the magnitude and position of damage [12]. To validate the method, two structures were chosen and modelled using FEA. In order to detect damage throughout the whole structure, especially some large, complicated structures, a methodology called global vibration-based structural damage detection [13, 14] has been proposed. The damage location and severity can be determined by finding the differences of structural dynamic characteristics between the intact and damaged structures [15]. A few natural frequencies were used and a methodology to non-destructively locate and estimate the size of damage in structures was proposed [16]. A detailed revision of the methods for damage detection can be found in [17]. Damage detection and estimation in structures based on incomplete modal data of a damaged structure can be done via a pattern search algorithm. The objective function based on the condensed mass and stiffness Matrices was formulated [18]. GAs were employed by many researchers for structural damage detection and localization based on model updating methods [19]. A damage detection and localization technique in beam-like structure using MAC (modal assurance criterion), COMAC (coordinate modal assurance criterion) and LFCR (Local Frequency Change Ratio) was introduced [20]. A genetic algorithm (GA) was used to detect damage in beam structure using three objective functions based on frequencies and eigenvectors [21]. In order to allow a comparison between different techniques, the following classification is proposed [22]: Detection, Localization, Assessment and Consequence.
In the present work, a new damage identification method is used by applying BAT algorithm to detect and locate single- and multiple-damage in beam-like structures. The objective functions used in the optimization process are based on vibration data of the structure. A finite element analysis is performed on simply supported beams discretized into 10 elements. Through the results obtained, we noticed that this method can accurately identify the damage, even though noise is present. This paper is organized as follows. In Section 2, methodological approach to the damage detection and localization problems is detailed. In Section 3, we present a numerical model of the beam structure. Implementation of BAT and PSO algorithm for damage detection and localization is given in Section 4. Results and discussion are shown in Section 5.
Fig. 1Methodological approach to the damage detection and localization using BAT algorithm
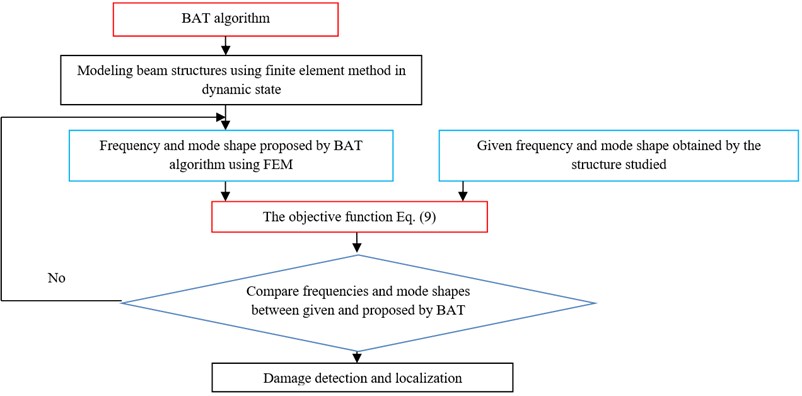
2. Methodological approach to the damage detection and localization using BAT algorithm
The optimization method refers to solving a problem in the best possible way. In most cases, the goal is to minimize or maximize an objective function based vibration analysis by choosing values for its variables within an acceptable range. The damage detection and localization procedures, which we propose here in, are carried out according to the following steps:
1) Expressing the damage by reducing Young’s modulus using FEM and calculating the natural frequencies and mode shapes (real damage).
2) Quantifying damage using BAT algorithm form the optimization problem.
3) Solving the inverse problem after providing frequencies and mode shapes (real damage) to the objective function in order to calculate damage locations and severity using BAT algorithm and FEM (estimated damage).
The Methodological approach to the damage detection and localization problems is illustrated by a flow chart as shown in Fig. 1.
3. Numerical model of the beam structure
We consider a simply supported unidirectionally [00] (AS4/3501-6) graphite epoxy beam. The finite element model is discretized in 10 elements. Each node of the finite element has three degrees of freedom; normal displacement along the axis, a rotation around the axis and the longitudinal displacement . Since the beam is macroscopically considered homogeneous, i.e. there is only one layer, the shear correction coefficient is the same as for isotropic beam [23]. The material properties and beam dimensions of simply supported unidirectionally [00] (AS4/3501-6) graphite epoxy beam [24] discretized into 10 elements are given in Table 1. The FEA model and the beam structure is shown in Fig. 2.
Fig. 2A simply-supported unidirectional [00] graphite-epoxy beam discretized into 10 elements
![A simply-supported unidirectional [00] graphite-epoxy beam discretized into 10 elements](https://static-01.extrica.com/articles/19717/19717-img2.jpg)
Table 1Dimension and material of beam
Ply property | Mean value |
Length (m) | 0.75 |
Width (m) | 0.03 |
Thickness (m) | 0.005 |
Longitudinal modulus (GPa) | 141.96 |
Shear modulus (GPa) | 6 |
Density (kg∙m-3) | 1600 |
Poisson’s ratio | 0.42 |
4. Implementation of BAT and PSO algorithms for damage detection
4.1. BAT algorithm
BAT algorithm is a recently introduced nature inspired algorithm. It is introduced by Yang and He [25] and inspired by behaviors of bats. The mammals, known as bats, have wings and a very good feature of generating echolocation. Yang and He [26] have used these characteristics of bats for the development of their BA. This algorithm is based on three important rules, which are given as:
1) For sensing distance, bat uses its echolocation capacity. It also uses echolocation to differentiate between food and prey and background barriers even in the darkness.
2) Bats used to fly randomly with some characteristics like a velocity, fixed frequency and loudness to search for a prey.
3) It also features the variations in the loudness from a large to minimum loudness.
In simulations, we use virtual bats naturally. We have to define the rules how their positions and velocities in a -dimensional search space are updated. The new solutions and velocities at time step are given by:
where [0, 1] is a random vector drawn from a uniform distribution. Here is the current global best location.
In the local search part, once a solution is selected among the current best solutions, a new solution for each bat is generated locally using random walk:
where [−1, 1] is a random number, while is the average loudness of all the bats at this time step.
The Algorithm parameters and Pseudo-code of BAT Algorithm (BA) are illustrated in Table 2.
Table 2Parameters and pseudo-code of BAT algorithm
Objective function based on (Natural frequencies and mode shape) Initialize the bat population ( 1, 2, ..., ) and Define pulse frequencyfi = 0.5 at Initialize pulse rates 0.5 and the loudness 0.5 while (Max number of iterations (200)) Generate new solutions by adjusting frequency, and updating velocities and locations/solutions [equations (1) to (3)] if (rand > ) Select a solution among the best solutions Generate a local solution around the selected best solution end if Generate a new solution by flying randomly (propose damage randomly in structure and calculate frequencies and mode shape). if (rand < & < ) Accept the new solutions Increase and reduce end if Rank the bats and find the current best end while Results and visualization of damage location in our structure |
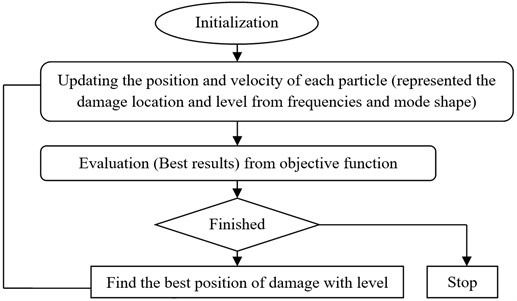
4.2. Particle swarm optimization (PSO)
The basic algorithm of the PSO works on a population of possible solutions called swarm, themselves called particles. These particles are randomly placed in the search space represented the damage location and level based on objective function (frequencies and mode shape). At each iteration, the particles move, taking into account their best position (egoistic movement) but also the best position of its vicinity [26].
In fact, the new speed is calculated from the following formula:
where: and are the velocities of the particle for iterations and 1. “Best particle” is the best position of the particle, “best vicinity” is the best position of its vicinity at iteration , “position particle” is the position of the particle at iteration . , , are constants, is randomly generated at each iteration and, in general, .
We can then determine the next position of the particle with the speed that we just calculated, i.e.:
where is the position of the particle at iteration .
The principle of the algorithm can be more easily seen through the flowchart given in Fig. 3.
Fig. 3PSO flowchart
4.3. The objective function of the optimization problem
The objective function is based on changes in natural frequencies and modal scale factor (MSF).
4.3.1. Changes in natural frequencies
Natural frequencies or eigenvalues are used as diagnostic parameters in structural assessment procedures using vibration monitoring. One great advantage of using only eigenvalues in the damage assessment of structures is that they are cheaply acquired and the approach can provide an inexpensive structural assessment technique. The objective function to be minimized is defined as follows [27]:
where – mode number (1, 2, 3,…, ), – test natural frequencies and – calculated natural frequencies.
The are the natural frequencies, which are applied to our damage detection system as inputs. An objective function equal to zero indicates an exact match between the measured and calculated frequencies.
4.3.2. Modal scale factor (MSF)
The modal scale factor is used as a diagnostic parameter in structural assessment procedures using vibration monitoring [28]:
where – calculated mode shape and – test mode shape
The objective function based on Modal Scale Factor and Changes in Natural Frequencies to be minimized in this algorithm is given by:
5. Results and discussion
In this study, instead of experimental measurements, numerically generated measurements, were used for a simply supported beam structure with 10 elements and different single- and multiple-damage scenarios. In the first scenario D1, damage is near the hinged support end, positioned in element 2 with damage rate 30 %. In the second scenario D2, damage is near the roller support in element 9 with damage rate 10 %. While in the third scenario D3, damage is spread over three elements; namely element 2 with damage rate 60 %, element 5 with damage rate 40 % and element 8 with damage rate 20 %. The objective function based on Modal Scale Factor and Changes in Natural Frequencies is minimized in this unconstrained optimization problem using BAT and PSO algorithms.
Fig. 4Damage results for single element damaged beam using BAT algorithm and PSO (Element 2, Damage rate 30 % (D1)

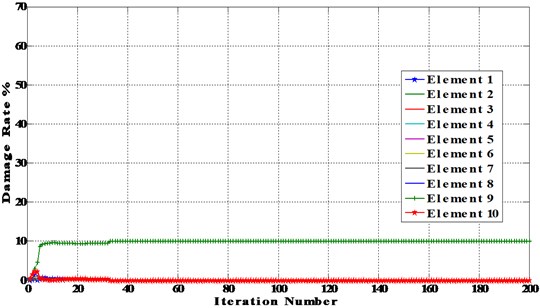
a) D1 using BAT algorithm 10 % with D1 PSO 10 %
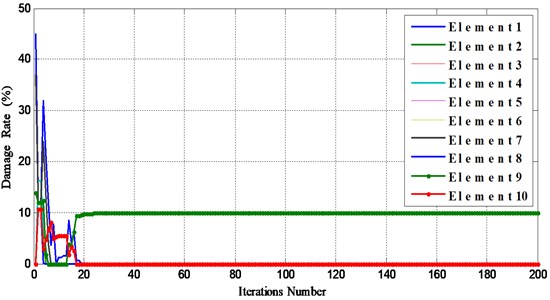
b) D1 using BAT algorithm 30 % with D1 PSO 30 %
5.1. Single damage scenarios
In this case, we created single damage in element 2 with damage rate 30 % (D1) and element 8 with damage rate 10 % (D2), as shown in Fig. 3, by finite element method and calculated the frequencies and mode shapes of the damaged structure. These parameters are used, as experimental data, in our approach for detecting and locating damage. The results obtained from optimization are shown in Figs. 4 and 5.
5.1.1. Damage scenario D1
The results of damage scenario D1 are shown in Figs. 4 and 5.
Fig. 5Damage results for single element damaged beam using BAT and PSO algorithms (Element 9, Damage rate 10 % (D2))

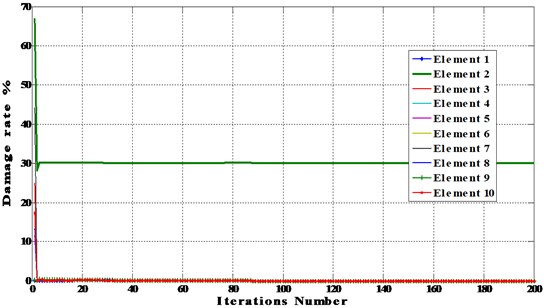
a) D2 using BAT algorithm
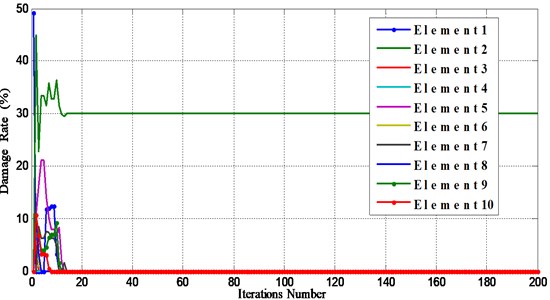
b) D2 using PSO algorithm
5.2. Multiple damage scenario
We created three damages in Elements 2, 5 and 8 (damage scenario D3) with different percentage 60 %, 40 % and 20 %, respectively using finite element method and we calculated the frequencies and mode shapes of the damaged structure using BAT and PSO algorithms. These parameters are used, as experimental data, in our approach for detecting three simulated damages. The results obtained from optimization are shown in Fig. 6.
Figs. 3-6 show that BAT algorithm is able to detect the location and the magnitude of damaged elements in all scenarios using complete data within the first few iterations (between 5-20 iterations) with high accuracy. We conclude that BAT algorithm is more efficient than PSO algorithm.
6. Damage detection with noise
In order to investigate the effects of noise on the results of our approach (Eq. (10)), the th noise response (noisy), is simulated as [28]:
where is the noise level and is a random number in the interval [−1, 1]. In this study σ is considered as 5 % and 10 %.
Fig. 6Damage detection using BAT and PSO algorithms for multiple damage (Elements 2, 5 and 8 (D3))

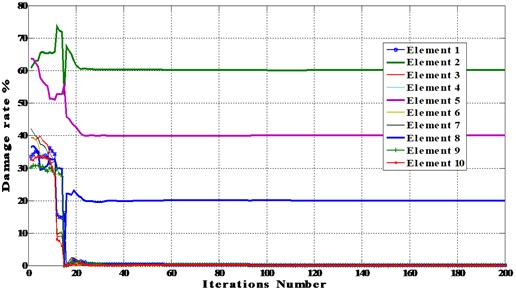
a) D3 using BAT algorithm
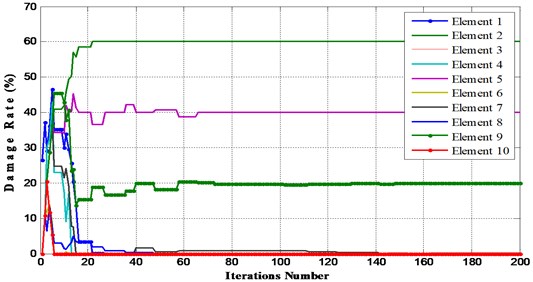
b) D3 using PSO algorithm
The results of the application of the algorithms to damage detection and localization for beam taking into account noise are plotted in Figs. 7 and 8, and Tables 3 and 4.
Table 3Single element damage with noise 5 % and 10 %
Elements | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Actual damage % | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | 0 |
Damage with noise 5 % | 0.3 | 0.24 | 0.13 | 0.21 | 0.14 | 0.13 | 0.17 | 9.987 | 0.11 | 0.12 |
Damage with noise 10 % | 0.74 | 0.59 | 0.39 | 0.47 | 0.41 | 0. 29 | 0. 23 | 9.971 | 0.52 | 0.21 |
Table 4Multiple-damage beam with noise level 5 % and 10 %
Elements | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Actual damage % | 0 | 60 | 0 | 0 | 40 | 0 | 0 | 20 | 0 | 0 |
Damage with noise 5 % | 0.25 | 59.71 | 0.32 | 0.29 | 39.82 | 0.312 | 0.384 | 19.91 | 0.29 | 0.271 |
Damage with noise 10 % | 0.370 | 59.24 | 0.410 | 0.31 | 39.71 | 0.381 | 0.401 | 19.83 | 0.322 | 0.381 |
6.1. Single damage scenario
For single damage scenario with noise, the stiffness of element 8 was reduced by 10 percent with noise level of 5 % and 10 %.
The Optimization results for single element damaged beam with noise level of 5% and 10% using BAT algorithm are shown in Fig. 7 and Table 3.
Fig. 7Single element damaged beam with different noise level
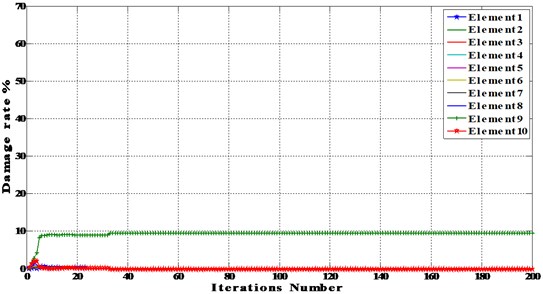
a) Noise 5 %
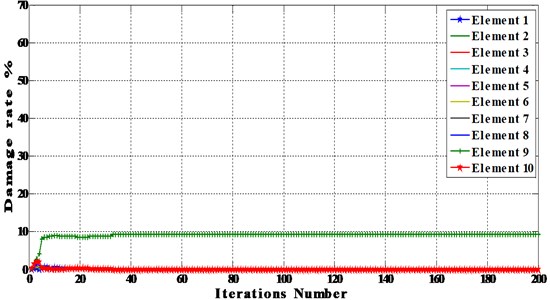
a) Noise 10 %
6.2. Multiple damage scenario
Optimization results for multiple damage beam with noise level of 5 % and 10 % using BAT algorithm are shown in Fig. 8 and Table 4.
For multiple damage scenario with noise, the stiffness of elements 2, 5 and 8 were reduced by 60 %, 40 % and 20 %, respectively with noise level of 5 % and 10 %.
From the results, we can observe that, when noise is taken into account in the damage detection problem, our approach based on BAT algorithm can detect the damage locations with good accuracy.
Khatir Samir, has conducted the research work presented in this paper in the framework of his Ph.D. research degree. Belaidi Idir has directed and supervised this research work, contributed in the conception, design and proposed methods of the work during his Ph.D. studies at LEMI in Boumerdes University, Algeria. Roger Serra has supervised this research work, contributed in the vibration analysis of the work and directed the first author during his research stay at LMR Laboratory INSA Centre Val de Loire, France. Magd Abdel Wahab, has supervised this research work, contributed in the conception and design of the work and directed the first author during his research stay at Ghent University, Belgium. Khatir Tawfiq has supervised this research work, contributed in the dynamic analysis of the work and Matlab programming.
Fig. 8Multiple damage beam with different noise level
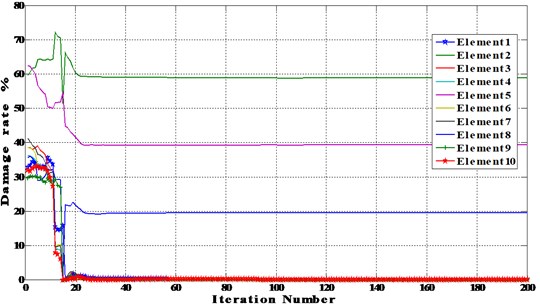
a) Noise 5 %
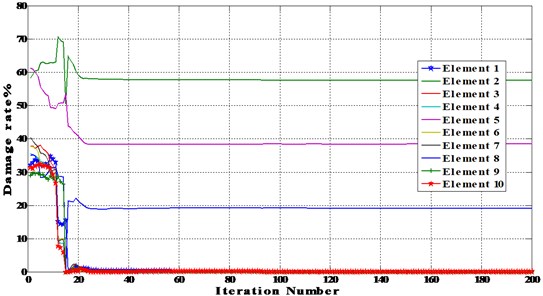
a) Noise 10 %
7. Conclusions
In this paper, an inverse problem method is proposed in order to detect and estimate damages in beam-like structures using PSO algorithm and new powerful algorithm called BAT algorithm. Several damage scenarios are considered to find the effect of damage severity and number of damaged elements. The BAT algorithm and PSO evaluates the location and severity of damage by minimizing an objective function based on the natural frequencies and mode shapes for undamaged and damaged tested beam with and without noise and considering different damage scenarios. The results showed high accuracy of the method using BAT algorithm, even when multiple-damage is present, within the first few iterations. When noise is taken into account in the damage detection problem, our approach based on BAT algorithm can detect the damage locations correctly with high accuracy.
References
-
Yang X.-S. Nature-Inspired Metaheuristic Algorithms. Luniver Press, 2008.
-
Yang X.-S. A New Metaheuristic Bat-Inspired Algorithm. Studies in Computational Intelligence. Springer Berlin, Vol. 284, 2010, p. 65-74.
-
Musikapun P., Pongcharoen P. Solving multi-stage multi-machine multi-product scheduling problem using bat algorithm. 2nd International Conference on Management and Artificial Intelligence, Vol. 35, 2012.
-
Tsai P. W., et al. Bat algorithm inspired algorithm for solving numerical optimization problems. Applied Mechanics and Materials, Vol. 148, Issue 149, 2011, p. 134-137.
-
Yang X. S. Bat algorithm for multi-objective optimization. International Journal of Bio-Inspired Computation, Vol. 3, Issue 5, 2011, p. 267-274.
-
Bora T. C., Coelho L. S., Lebensztajn L. Bat-inspired optimization approach for the brushless DC wheel motor problem. IEEE Transactions on Magnetics, Vol. 48, Issue 2, 2012, p. 947-950.
-
Hajela P., Soeiro F. J. Structural damage detection based on static and modal analysis. AIAA Journal, Vol. 28, Issue 4, 1990, p. 1110-1115.
-
Chakraverty S., Singh V. P., Sharma R. K. Regression based weight generation algorithm in neural network for estimation of frequencies of vibrating plates. Computer Methods in Applied Mechanics and Engineering, Vol. 195, 2006, p. 4194-4202.
-
Sazonov E. S., Klinkhachorn P., Halabe U. B. Genetic algorithms based parameter optimization of a non-destructive damage detection method. Proceedings of the Thirty-Fourth Southeastern Symposium on System Theory, 2002.
-
Cawley P., Adams R. D. The location of defects in structures from measurements of natural frequencies. The Journal of Strain Analysis for Engineering Design, Vol. 14, Issue 2, 1979, p. 49-57.
-
Jones Messina I. A., Williams E. J. Damage detection and localization using natural frequency changes. Proceedings of Conference on Identification in Engineering Systems, Swansea, UK, 1996, p. 67-76.
-
Iturrioz I., Pasquetti E., Doz G., et al. Evaluation of structural damage through changes in dynamic properties. International Symposium on Nondestructive Testing Contribution to the Infrastructure Safety Systems in the 21st Century, 1999, p. 162-166.
-
Carden E. P., Fanning P. Vibration based condition monitoring: a review. Structural Health Monitoring, Vol. 3, Issue 4, 2004, p. 355-377.
-
van der Auweraer H. International research projects on structural damage detection. Damage Assessment of Structures Key Engineering Materials, Vol. 204, Issue 2, 2001, p. 97-112.
-
Yam L. H., Yan Y. J., Jiang J. S. Vibration-based damage detection for composite structures using wavelet transform and neural network identification. Composite Structures, Vol. 60, Issue 4, 2003, p. 403-412.
-
Kim J. T., Ryu Y. S., Cho H. M., Stubbs N. Damage identification in beam-type structures: frequency-based method vs. mode-shape based method. Engineering Structures, Vol. 25, Issue 1, 2003, p. 57-67.
-
Doebling S. W., Farrar C. R., Prime M. B., Shevitz M. B. D. W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics. A Literature Review. Los Alamos National Laboratory Report, LA-13070-MS, 1996.
-
Kourehli S. S., Amiri G. G., Ghafory-Ashtiany M., Bagheri A. Structural damage detection based on incomplete modal data using pattern search algorithm. Journal of Vibration and Control, Vol. 19, Issue 6, 2012, p. 821-833.
-
Friswell M. I., Penny J. E. T., Garvey S. D. A combined genetic and eigensensivity algorithm. Computers and Structures, Vol. 69, Issue 5, 1998, p. 547-556.
-
Khatir S., Serra R., Belaidi I. Détection et localisation de défauts dans des structures poutres par analyse vibratoire. Proceeding of 4ième Congrès Algérien de Mécanique, At Mascara, Algérie, 2013, (in French).
-
Khatir S., Belaidi I, Serra R., Benaissa B., Ait Saada A. Genetic algorithm based objective functions comparative study for damage detection and localization in beam structures. Journal of Physics: Conference Series, Vol. 628, Issue 1, 2015, p. 012035.
-
Doebling Scott W., Farrar Charles R., Prime Michael B. A summary review of vibration-based damage identification methods. Shock and Vibration Digest, Vol. 30, Issue 2, 1998, p. 91-105.
-
Rikards R. Analysis of Laminated Structures Course of Lectures. Riga Technical University, 1999.
-
Gayathri P., Umesh K., Ganguli R. Effect of matrix cracking and material uncertainty on composite plates. Reliability Engineering and System Safety, Vol. 95, 2010, p. 716-28.
-
Yang X. S., He X. Bat algorithm: literature review and applications. International Journal of Bio-Inspired Computation, Vol. 5, Issue 3, 2013, p. 141-149.
-
Plevris V., Batavanis A., Papadrakakis M. Optimum design of steel structures with the particle swarm optimization method based on EC3’. Computational Methods in Structural Dynamics and Earthquake Engineering, Corfu, Greece, 2011.
-
Baghmisheh M. T. V., Peimani M., Sadeghi M. H., Ettefagh M. M. Crack detection in beam-like structures using genetic algorithms. Journal of Applied Soft Computing, Vol. 8, 2008, p. 1150-1160.
-
Gerist S., Naseralavi S. S., Salajegheh E. Basis pursuit based genetic algorithm for damage identification. International Journal of Optimization in Civil Engineering, Vol. 2, Issue 2, 2012, p. 301-319.
