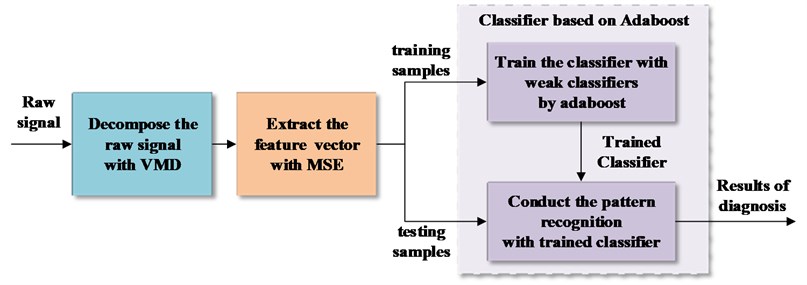
Abstract
Accurate and efficient fault diagnosis is of great importance for gearbox. This study proposed a fault diagnosis based on variational mode decomposition (VMD) – multiscale entropy (MSE) and adaboost algorithm. First, the VMD is employed to decompose the raw signal in time-frequency domain. Then, MSE is computed to generate the feature vectors. Finally, the classifier based on adaboost is training and several weak classifiers form a strong classifier to realize the fault diagnosis. The feasibility and accuracy of the method is validated by the data from the Prognostics and Health Management Society for the 2009 data challenge competition.
1. Introduction
Gearbox is the representive and crucial devices of rotary machinery. During the operation, the defects of gearbox may result in degradation, breakdown and even safety issues. Thus, the condition monitoring and fault diagnosis are essential for gearbox. Features hidden in the vibration signal can demonstrate the performance and degradation of gearbox. However, due to the complexity of gearbox structure and the intricate of fault mechanism, it is difficult to identify the characteristics of the vibration signal and extract the feature by traditional signal processing method.
Empirical Mode Decomposition (EMD) and Local Characteristic-scale Decomposition (LCD) have a widely application for many years. But the mode mixing and end point effect are unavoidable. Moreover, the sampling frequency has a greater impact on the results of decomposition. To overcome the limitations of above-stated method, variational mode decomposition (VMD), a newly signal processing method, is proposed by K. Dragomiretskiy in 2014 [1]. VMD is a non-recursive and adaptive variational signal decomposition algorithm. By looking for an ensemble of modes and their respective center frequencies, VMD can decompose a multi-component signal into a discrete number of sub-signals. Therefore, in each mode, the signal is compact around the center frequency [2]. VMD method is much more robust to the noise and sample.
Entropy is a measure of the complexity of time series. Approximate entropy (ApEn) and sample entropy (SpEn) presented in recent years are practical ways to estimate the signal’s complicacy. However, these methods are not applicable in some cases, especially when the signal has multiscale complex characteristics. Focusing on the shortcomings of traditional method, M. Costa introduced the multiscale entropy (MSE) [3]. MSE compute the entropy values (SpEn) from each of the individual time series scale, thus it can identify the overall complicacy of the signal comprehensively [4].
The performance of classifier influences the accuracy and efficiency of diagnosis. Boosting is a new ensemble technique and has powerful ability to improve the accuracy of basic learning algorithms. Adaboost, one of the widely applied boosting algorithms, connects the weak classifier with low accuracy and constructs a strong classifier with high accuracy without any prior knowledge. Due to simple and efficient, adaboost is commonly accepted and employed extensively.
In order to process the complex vibration signal of gearbox and achieve the fault diagnosis, the approach based on VMD-MSE and adaboost is proposed. The rest of the paper consists 3 sections. Section 2 describes the framework of fault diagnosis method and illustrates the methodology as well as the related mathematics; Section 3 shows a case study in which the method is validated by experimental data; Section 4 summarized the paper and future works are discussed.
2. Methodology
The proposed method is summarized in Fig. 1. First, the raw signal is analyzed in time-frequency domain based on VMD. Then, the MSE is calculated as the feature vector. Finally, the classifier is trained by adaboost algorithm and the trained classifier is employed to realize the fault diagnosis.
Fig. 1The procedure of fault diagnosis proposed
2.1. Signal processing by VMD
A raw signal is decomposed by VMD into finite number of band-limited intrinsic mode functions (IMFs). Viewed from the point of Fourier domain, the method is generalization of the Wiener filter into multiple, adaptive bands. With the optimization of alternating direction method of multipliers (ADMM), the adaptive decomposition is realized.
VMD process is divided into two steps: the establishment and solution to the constrained variational problem. The problem is written as follows:
Subjected to .
To transform the constrained variational problem into an unconstrained variational problem, the quadratic penalty and Lagrangian multipliers are introduced to Eq. (1). The augmented Lagrangian is expressed as follows:
The Eq. (2) is solved by iterate search with ADMM.
From solution, the mode and the century frequency are written respectively as follows:
The detail principle and process of the VMD algorithm can be found in [1].
2.2. Feature extraction with MSE
On the basis of SpEn, MSE is introduced into two steps in . Costa’s work [3].
Step 1. Coarse-graining process for the original time series :
Newly constructed time series is as follows:
where is the scale factor.
Step 2. SpEn algorithm is performed in each and MSE is defined based on the SpEn value.
2.3. A classifier based on adaboost algorithm
A brief discerption of classifier based on adaboost algorithm is given here. Given: where , .
1. Initialize the weight .
2. For ( is the number of boosting rounds):
• Train weak classifier using the weights .
• Obtain the weak classifier with error:
• Compute:
• Update:
where is a normalization factor.
3. Output:
3. Case study
To validate the effectiveness of the presented method, public gearbox vibration signals from the 2009 PHM Conference Data Analysis Competition are used. Data of helical gear with 50 Hz speed and high load are chosen as the original signal. After preprocessing, 225 sets of healthy data (from helical1) and 225 sets of faulty data (from helical3), including idler gear broken, combination bearing and input shaft bent, were acquired.
Defined the number of modes as . The center frequency was computed under different . When is greater than or equal to three, modes with similar center frequency appeared. Therefore, each original vibration signal was processed by VMD under 3. Fig. 2 shows the decomposition results of the signal from healthy gearbox.
Fig. 2The VMD decomposition diagram
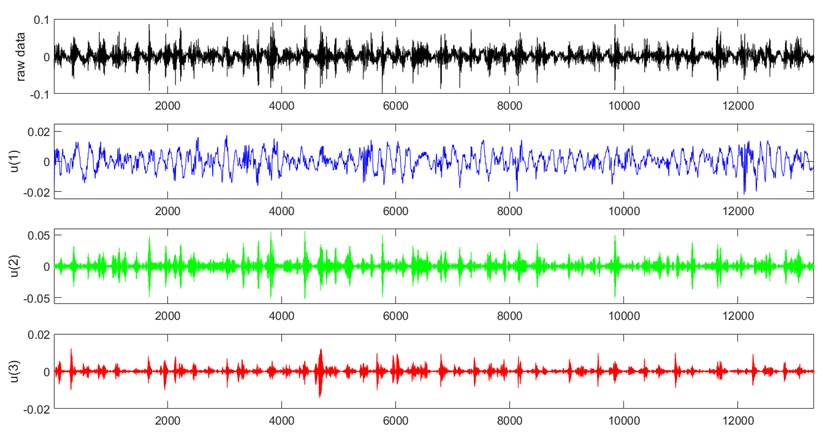
Then, the MSE value was extracted under each mode to form the eigenvector. In this case, a three-dimensional array as feature vector were generated for diagnosis. For healthy and faulty status, 225 eigenvectors were obtained respectively, and totally 450 eigenvectors were obtained.
400 eigenvectors as the training data to train the classifier based on adaboost. The label of the 200 healthy eigenvectors was set to 1 and the label of the 200 faulty eigenvectors was set to 1. The classifier based on dynamic threshold was selected as the weak classifier in the adaboost algorithm. Fig. 3 shows the classification error of training data. As the number of iterations increases, the classification error decreases gradually, and finally becomes to 0. This shows that after training, the adaboost algorithm improved the classification accuracy. A strong classifier is constructed based on multiple weak classifiers.
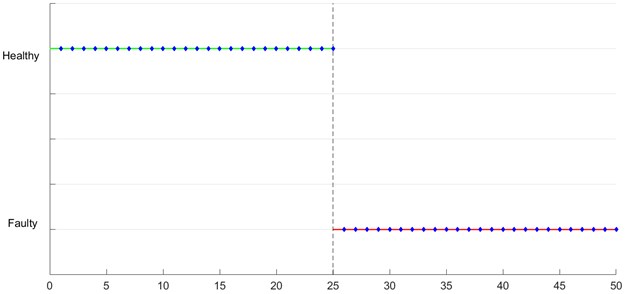
Finally, the other 50 feature vectors as testing data were sent to the classifier improved by adaboost. As shown in the Fig. 4, there are no testing sample of the miss-judgement based on the trained classifier among the 50 testing samples. The diagnosis accuracy was 100 %.
Fig. 3Classification error versus number of weak classifier
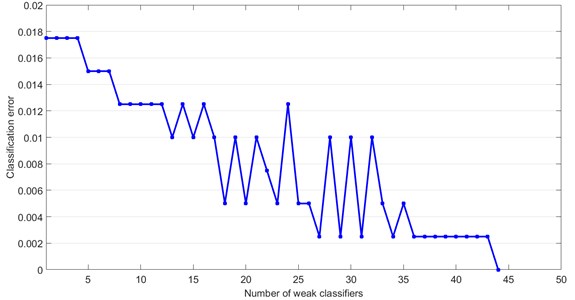
Fig. 4The results of fault diagnosis
4. Conclusions
This paper introduced a methodology for gearbox diagnosis. The methodology involves the signal processing method by VMD, which has high-robustness, and the feature extraction method by MSE. A classifier based on adaboost algorithm is presented as well, and the classifier is applied for fault diagnosis. The methodology was validated by the gearbox data from 2009 PHM Conference Data Analysis Competition.
In the future work, the VMD and MSE algorithm can be improved to optimize the selection of parameters. At the same time, using the framework of adaboost, choose different weak classifier adapt to different situations to improve the performance of classifier.
References
-
Dragomiretskiy K., Zosso D. Variational mode decomposition. IEEE Transactions on Signal Processing, Vol. 62, Issue 3, 2014, p. 531-544.
-
Zhang M., Jiang Z., Feng K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mechanical Systems and Signal Processing, Vol. 93, Issue 460, 2017, p. 460-493.
-
Costa M., Goldberger A. L., Peng C. K. Multiscale entropy analysis of complex physiologic time series. Physical Review Letters, Vol. 89, Issue 6, 2002, p. 68102.
-
Michael, Busa A., Richard, et al. Multiscale entropy: A tool for understanding the complexity of postural control. Journal of Sport and Health Science, Vol. 5, Issue 1, 2016, p. 44-51.
-
Guo H., Li Y., Li Y., et al. BPSO-Adaboost-KNN ensemble learning algorithm for multi-class imbalanced data classification. Engineering Applications of Artificial Intelligence, Vol. 49, 2015, p. 176-193.
-
Nayak D. R., Dash R., Majhi B. Brain MR image classification using two-dimensional discrete wavelet transform and AdaBoost with random forests. Neurocomputing, Vol. 177, 2016, p. 188-197.
Cited by
About this article
This study is supported by the Fundamental Research Funds for the Central Universities (Grant Nos. YWF-17-BJ-J-42 and YWF-16-BJ-J-18) and the National Natural Science Foundation of China (Grant Nos. 51605014 and 51575021), as well as the Technology Foundation Program of National Defense (Grant No. Z132013B002).
