Abstract
Vibration suppression of face gear drives is always one of study focuses of face gear dynamics. Thus, in the study, a solution of active vibration suppression associated with web structures on face gear drives is proposed, and an example case of face gear drives associated with the proposed solution is simulated. The results indicate effects of the proposed solution on face gear dynamic behaviors are significant. These contributions would benefit to improve face gear vibration suppression studies.
1. Introduction
Face gear dynamics is focused by many scholars, due to operating conditions of first-stage gear drives in helicopter main gear boxes. There are a vast of lectures discussing dynamic behaviors of face gear drives in the past few years [1-8]. However, the solutions of active vibration suppression on face gear drives are not constructed. Thus, in the study, a solution of active vibration suppression associated with web structures on face gear drives is proposed, and dynamic behaviors of an example case of face gear drives associated with the proposed solution are simulated. The results indicate the fidelity of the proposed solution of active vibration suppression of face gear drives could be accepted. These contributions would be helpful to improve vibration suppression studies of face gear drives in the future.
2. Web structures
Based on a viewpoint, namely, the rotation of the wheel body being an important factor on flexibilities of gear teeth [9], namely, mesh stiffness and STE (Static Transmission Error) being affected by gear wheel body flexibility sharply, a solution of active vibration suppression associated with web structures on face gear drives, as shown in Fig. 1, is proposed.
Fig. 1The proposed vibration active control solution
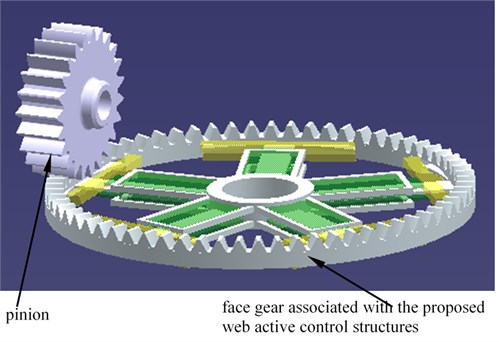
a) A face gear drive associated with web active control structures
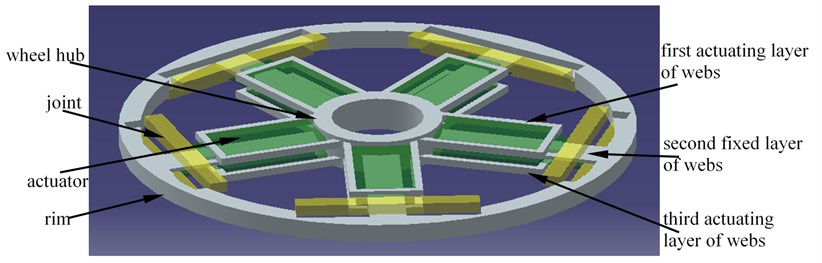
b) The local view of web active control structures
As illustrated in Fig. 1, a face gear web could be divided into two version layers. one is an actuating layer, such as the first and the third layers, namely, the layer associated with actuators and not contacted with rims at initial states, the other is a fixed layer, such as the second layer, meaning, the layer without actuators and contacted with rims at initial states.
3. Dynamic model
In order to assess effects of the proposed solution on face gear dynamic behaviors, employed the lumped-mass method, a four DOFs dynamic model of face gear drives, as shown in Fig. 2, is established, and the active control is introduced into the dynamic model by STE.
Fig. 2A four DOF dynamic model of face gear drives
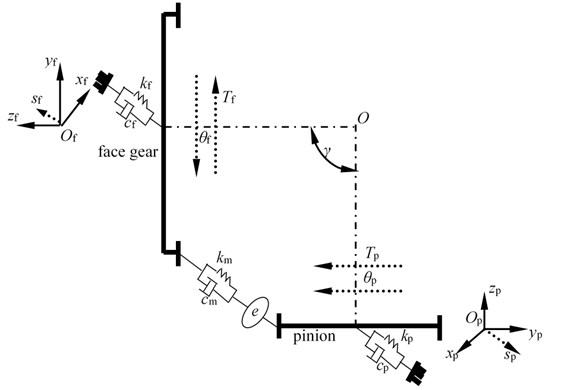
As illustrated in Fig. 2, is a torsion DOF, is a bending DOF. is a torsion, is a bending stiffness, is a bending damping, subscript and express face gears and pinions, respectively, is a mesh stiffness of face gear drives, is a mesh damping of face gear drives, is a shaft angle of face gear drives, and is a STE, which could be defined as:
where is a error caused by complex tooth deformations, and is a error caused by rotation deformations of wheel bodies of face gear drives.
Based on Fig. 2, the mathematic equations of the dynamic model could be derived by:
where is a quality, is a radius of basic circles, is a moment of inertia, and could be deduced as:
4. Simulation and analysis
In order to assess effects of the proposed active vibration suppression on dynamic behaviors of face gear drives, parameters of an example case of face gear drives associated with web structures are listed in Table 1.
Table 1Parameters of an example case of face gear drives
Types | Symbol Name | Values | Unit |
Geometry parameters | Modulus | 2 | mm |
Pressure angle | 25 | ° | |
Pinion tooth number | 23 | – | |
Face gear tooth number | 67 | – | |
Face gear inner radius | 64 | mm | |
Face gear external radius | 70 | mm | |
Shaft angle | 90 | ° | |
Material parameters | Elastic modulus | 210000 | MPa |
Poisson ratio | 0.3 | – | |
Shear modulus | 80 | MPa | |
Operating conditions | Power | 15 | kW |
Input rotation speed | 3000 | r/min | |
Web structure parameters | Layer number | 3/5 | – |
Actuator number | 5/3 | – | |
Web thickness | 8 | mm | |
50 | mm | ||
10 | mm | ||
35 | mm | ||
20 | mm |
According to Table 1, Eqs. (1-3) and two version active control methods, namely, STE key point active control (the first version) and STE procession active control (the second version), the dynamic behaviors and the dynamic mesh forces of the example case are simulated, as shown in Fig. 3 and Fig. 4, respectively.
In Fig. 3, compared Fig. 3(a) with Fig. 3(b), the forms are similar, the amplitudes are reduced, and the escape quantities of the small rings are reduced. Meanwhile, compared Fig. 3(a) with Fig. 3(c), the forms are not similar, due to the added rings in the big cycles, the amplitudes are still reduced, and the escape quantities of the small rings are increased.
As illustrated in Fig. 4, after the first version active control method, the spectral distribution form of the dynamic mesh force is not changed, and the amplitudes versus frequencies are almost reduced. While, after the second version active control method, the spectral distribution form of the dynamic mesh force is changed.
Fig. 3Dynamic behavior simulations of the example case
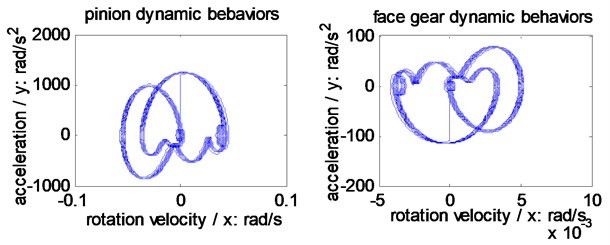
a) Without any active control
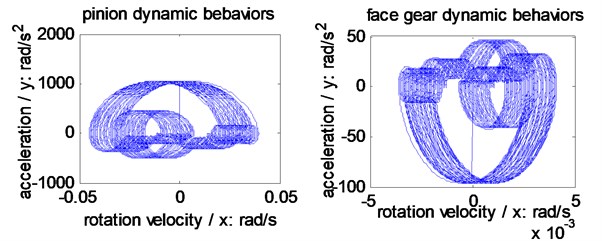
b) The first active control method
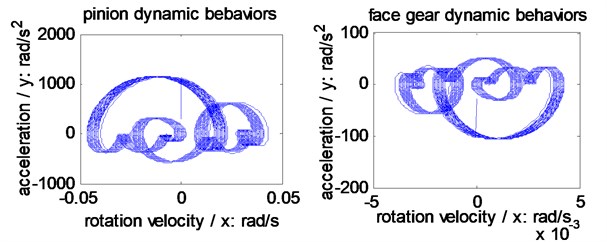
c) The second active control method
Fig. 4Dynamic mesh force simulations of the example case
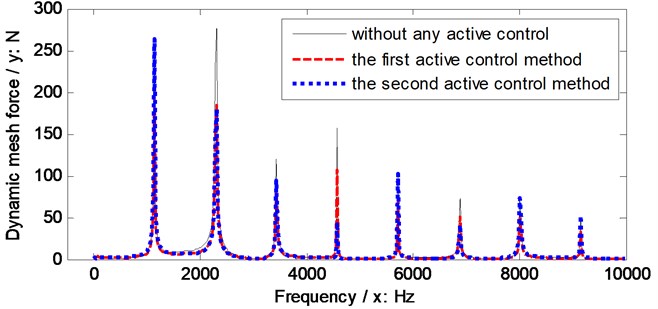
5. Conclusions
In the study, two works can be extracted as follows:
1) A solution of active vibration suppression associated with web structures on face gear drives is proposed.
2) Vibration suppression effects of face gear drives are significant by the proposed solution.
These contributions would be helpful to improve vibration suppression studies of face gear drives in the future.
References
-
Hu Z. H., Tang J. Y., Chen S. Y., Lei D. C. Effect of mesh stiffness on the dynamic response of face gear transmission system. Journal of Mechanical Design, Vol. 135, Issue 7, 2013, p. 1-7.
-
Wang Z., Chen Q., Lin J. C., Yang L. L. Study of the dynamic behavior of face gear transmission system. Applied Mechanics and Materials, Vol. 268, 2013, p. 1063-1066.
-
Jin G. H., Zhu R. P., Bao H. Y. Nonlinear dynamical characteristics of face gear transmission system. Journal Central South University, Vol. 5, Issue 41, 2010, p. 1807-1813, (in Chinese).
-
Yang Z., Wang S. M., Fan Y. S., Liu H. X. Vibration characteristics of face-gear transmission system with parametric excitation. Journal of Chongqing University, Vol. 35, Issue 1, 2011, p. 26-35, (in Chinese).
-
Yang Z., Wang S. M., Fan Y. S., Liu Bifurcation H. X. characteristics of face-gear transmission system. Journal of Harbin Institute of Technology, Vol. 3, Issue 43, 2011, p. 107-110, (in Chinese).
-
Li X. Z., Zhu R. P., Li Z. M. Q., Jin G. H. Influence of frictional coefficient on vibration characteristic of face gear transmission system. Journal of Vibration Engineering, Vol. 27, Issue 4, 2014, p. 584-588, (in Chinese).
-
Zhang L., Zhu R. P., Li Z. M. Q. Research on natural frequency of torsional vibration of torque-split face gear transmission system. Jiangsu Machine Building and Automation, Vol. 41, Issue 5, 2012, p. 21-24, (in Chinese).
-
Li Zhengminqing, Liu Shuang, Zhu Rupeng, Xiu Xiaodong Investigations of dynamic behaviors of face gear drives associated with pinion dedendum fatigue cracks. Shock and Vibration, 2016, https://doi.org/10.1155/2016/3173860.
-
Zhu X. L., E. Z. K. Analysis of Load Capacity of Gears. Higher Education Press, Beijing, 1992, (in Chinese).
About this article
The authors are grateful for the financial support provided by the National Natural Science Foundation of China under No. 51775264. In addition, the authors declare that there is no conflict of interests regarding the publication of this article.
