Abstract
Conventional reliability demonstration test (RDT) based on statistical method is widely used in industry as it is simple and convenient to apply. But for products with high reliability and long life, this test method fails to satisfy the demand for short cycle and low cost, and is liable to cause the phenomenon of over-test and short-test. This paper gives a method to determine the accelerated stress profile for RDT under multiple stresses and mechanisms, making it faster to make decision of accept or reject. By raising the levels of sensitive stresses that the product would experience, the test time can be cut down remarkably. We can derive the overall acceleration factor based on the narrow reliability bounds theory. Then we choose the test plan referring to GJB 899A. Furthermore, combined with the reliability qualification test (RQT) profile, the accelerated test profile is acquired. An example is given to illustrate the superior performance of the proposed method over traditional methods.
1. Introduction
The problem of reliability demonstration of a new product using existing test methods is well known in manufacturing industry. RDT is composed of the test plan and decision rules, and as the total test time of this test type is pre-determined, time-censoring (type-I censoring) is commonly used in the engineering applications [1]. However, for advanced products with high reliability and long lifetime, test duration and sample size become time and cost prohibitive [2]. The difficulty is overcome by accelerated test where test units are subjected to higher stress levels than normal for rapid failures [3]. Moreover, traditional statistical method cares nothing about the individuality of products, but need massive test samples [4]. As the failure is always caused by multiple mechanisms, there is no guidance on what the environmental and operational stresses should be applied during the RDT, and how the mean time to failure (MTBF) related to environment profile and sensitive stresses. So, it is significant to develop a new method to determine the accelerated stress profile for the long-life electronic products.
Many researchers pay attention to accelerated demonstration testing. Willis derives a modified sequential probability ratio test (SPRT) using a simple Gaussian Markov process for pipeline leak detection [5]. Kang synthesizes risks from life distribution and model selection and finds the equivalent dispersion of system level acceleration factor (AF), then the system level verification testing with one sample has been designed [6]. Yadav facilitates the development of reliability test plan by bring three-dimensional understanding of the product design while utilizing existing information and knowledge [7]. Milena designs the accelerated sequential testing to demonstrate product’s reliability regarding its expected operational and environmental stresses with the required confidence in the test result [8]. David considers the step-stress model under time-censoring when the different risk factors have s-independent generalized exponential lifetime distributions [9]. Most of the relative literatures focus on time-censoring, failure-censoring, or SPRT under constant or step-stress accelerated stress, and little attention has been devoted to the determination of the accelerated test profile under multiple stresses and mechanisms.
In this study, we propose a method to design reliability demonstration test profile based on statistical approach as well as physics of failure (PoF), which significantly shortens the test time and effectively cuts the cost. Sensitive stress and main failure mechanism are determined by failure mode, mechanism and effect analysis (FMMEA). After determining the acceleration factors and choosing the statistical plan in GJB 899A, we establish the accelerated demonstration test profile. A case example is made to present the procedure, stating the proposed method is better than traditional statistical method, and it can also avoid the phenomena of over-test and short-test in verification.
2. Determination of sensitive stress and main failure mechanism
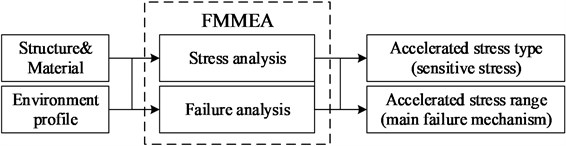
Stress and failure analysis based on PoF aim at providing an approach for determining the main sensitive stresses which lead to a certain failure mechanism of a component for specific function [10]. FMMEA methodology is used to identify and classify known or potential failure modes and mechanisms based on the physical or functional points of view, to prioritize all the mechanisms to determine the main failure mechanisms and their related operating conditions and environment parameters, and to provide information for making risk management decisions [11]. Fig. 1 illustrates the flow chart for determining accelerated stress range and type, including stress sensitivity analysis and failure effect analysis.
First of all, we build the typical environment profile for the product based on mission profile. Then combined with products’ structure and material information, we can analyze sensitive stress and main failure mechanism by according to risk priority number (RPN): severity (S), occurrence (O) and detection (D). Finally, the accelerated stress type and range are determined.
Fig. 1Flow chart for stress and failure analysis based on PoF
3. Formulation of test profile of accelerated demonstration test
For most electronic products, temperature and vibration are the primary environment stresses leading to failure. So, we take thermal cycling, thermal dwell and vibration for example to show the use of acceleration models. Based on the narrow reliability bounds theory, we can calculate the overall AF analogously, and then we choose an appropriate time-censoring statistical test plan from GJB 899A [12]. Combined with the stress profile in RQT, the accelerated demonstration testing profile is acquired.
3.1. Calculation of AF for each sensitive stress
1) Thermal cycling. According to JESD94A [13], the thermal cycling follows Norris-Landzberg model:
where , are thermal amplitudes, , are temperature ramp rates, , are highest exposure temperatures.
2) Thermal dwell. For simplicity, the product is exposed to only a high temperature. Acceleration model of thermal dwell follows Arrhenius model [14]:
where , are exposure temperatures, is activation energy (eV), is Boltman’s constant = 8.617×10-5eV/K.
3) Vibration. According to reliability methodology for electronic systems of FIDES [15], the AF for random vibration is given by:
where is root mean square vibration amplitude in the environment considered, and is reference vibration amplitude.
3.2. Determination of overall acceleration factor and accelerated stress level
It is important to notice the standard practice of multiplying all of the acceleration factors, which would provide an overly estimated overall test acceleration. It is intuitively apparent that this standard practice acceleration is extremely unrealistic and may lead to grossly erroneous reliability conclusions [16]. According to the narrow reliability bounds theory [17], the overall AF can be calculated analogously. As the computing method of overall AF is very complicated, independence assumption and weakest-link model are usually used to simplify calculations. The more complete the information about the life distribution, the tighter the bounds can be made. Actually, different operational and environmental stresses that the system is exposed to are surely related to each other, and the overall AF changes continuously with the degree of correlation. Then the continuous process can be simply divided into five stages with different formulas based on their relevancy. If the system is expected to be encountered types of stresses, AF for each stress is , ,…, , and satisfy . Therefore, the overall AF mathematical model based on narrow reliability bounds theory is expresses as:
The correlation of the system’s sensitive stresses is affected by structure, material, failure mechanisms and failure modes, etc. By analyzing the practical situation, and we can determine the corresponding formula.
3.3. Determination of parameters in accelerated test profile
As the required test duration is apparently time prohibitive, each of the expected environmental stresses to be applied in test should be accelerated. By raising stress level in the condition of unchanging failure mechanism of the product, the test time for each environment stress can be calculated. Select specimens randomly from the same batch of products to carry out accelerated life test (ALT).
After the statistical test plan is determined, the total test time accumulated on all of the test units is . The test time of a cycle in RQT is , then the total cycles of the RQT are:
1) Number of test cycles. Convert the cycle number in RQT into accelerated conditions, and the number of test cycles is equal to number of thermal cycles. Thus, the number of accelerated stress profile cycles is:
where and are the accelerated and normal stress profile cycle number respectively.
2) Thermal dwell duration in a cycle. For stress synergism and determining thermal dwell at the high temperature, we combine thermal exposure with the thermal cycling, distributing the thermal exposure over the high temperature of the thermal cycling. In a cycle of RQT, the thermal dwell duration for each cycle in accelerated condition is given by:
3) Vibration duration in a cycle. The vibration duration for each cycle in accelerated condition is given by:
4) Duration of a test cycle. The duration of an accelerated cycle is expressed as:
where is the duration of low temperature, which should make sure the product is completely cold during the low temperature stage, and is the total duration of temperature change.
5) The test time of the accelerated test. The total duration of the step-stress accelerated test is expressed as:
4. Case example
In the section, we illustrate the proposed test plan with a dedicated time-frequency device of a vehicle military communication equipment, whose lifetime follows exponential distribution. The reliability goal is given by MTBF ≥ 9000 h, namely 9000 h.
By FMMEA on the equipment, the main failure stresses are temperature and vibration. Therefore, the accelerated stresses are thermal dwell, thermal cycling and vibration. Moreover, the main failure mechanisms are fatigue leading to capacitor’s short circuit, and electromigration resulting in resistor’s open circuit. Combined with the operating limits of products and the load capacity of the test equipment, the accelerated temperature stress should not exceed 85 ℃ and vibration stress should below 12 grms.
GJB 899A-2009 provides time-censoring, failure-censoring and sequential test plans, and we select the 17th statistical plan, of which the normal time-censoring test parameters and decision criterion are shown in Table 1.
According to the environment profile and analysis of sensitive stresses and main failure mechanism, the test profile of RQT is shown in Fig. 2. Required vibration can be translated into 30 min per axis vibration at 6 grms. The total test time of RDT is: 38700 h. A cycle time under normal condition is: 568 min. Then the numbers of RDT cycles are: 4088.
Table 1Statistical plan of RQT
No. of plans | Decision making risks | Discrimination ratio | Test time () | Decision failures | ||||
Nominal value | Actual value | |||||||
Rejection (≤) | Acceptance (≥) | |||||||
17 | 20 % | 20 % | 17.5 % | 19.7 % | 3.0 | 4.3 | 3 | 2 |
Fig. 2Test profile of RQT for the equipment

We choose 80 °C and 12 grms as the typical accelerated stresses, and assume 0.8eV. Then we calculate AF for each stress, which are shown in Table 2. To determine overall acceleration factor, it will be assumed that vibration and thermal cycling are stresses that would accelerated the same failure modes. That is to say they have strong correlation with each other, and they have weak correlation with thermal dwell. Therefore, the overall AF is calculated and a more realistic overall acceleration factor is achieved, that is 35.46.
Table 2Accelerated stress level and AFs of the device
Stress level | (°C) | (°C) | (°C/min) | (grms) | Thermal cycling | Thermal dwell | Vibration | Overall AF |
S0 | 55 | 90 | 5 | 6 | – | – | – | – |
SA | 80 | 115 | 10 | 12 | 2.5773 | 7.423 | 8 | 35.46 |
Table 3Comparison of non-accelerated RDT to the step-stress accelerated RDT
Stress type | No. of test cycles | Thermal dwell duration (min) | Vibration duration (min) | duration of a cycle (min) | Total test time (h) |
Non-accelerated | 4088 | 480 | 30 | 568 | 38700 |
Accelerated | 116 | 2279 | 132 | 2362 | 4567 |
Results and test comparison are presented in Table 3, where 11.5 min, 60 min. Obviously, the test time is significantly shortened by accelerating the multiple environmental stresses from 38700 h to 4567 h. The reliability demonstration test is then to be designed for the above MTBF. However, the test will not have to demonstrate the very high required MTBF = 9000 h, but the MTBF about 8.5 times lower MTBF. The accelerated test would have a duration of 4567 h compared to the non-accelerated test that would need a duration of 38700 h. And the reliability demonstration test profile is shown in Fig. 3.
Fig. 3Test profile of accelerated reliability demonstration test

5. Conclusions
In this paper, a methodology to determine the accelerated RDT profile for assembly level products under multiple environment stresses is proposed. A new method is established to determine comprehensive acceleration factor based on the narrow reliability bounds theory. Then the accelerated reliability demonstration plan and test profile combine conventional statistical demonstration method with PoF, which helps in focusing on sensitive environmental stresses and makes it faster to demonstrate the product’s reliability goal. The detailed process on the establishment of accelerated test profile under multiple stresses and mechanisms was illustrated with a case example, revealing it can remarkably cut down the test time and cost.
References
-
Jiang Tongmin Reliability and Life Test. National Defense Industry Press, Beijing, 2012, p. 230-240.
-
Nelson W. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis. Wiley, New York, 1990.
-
David Han Time and cost constrained optimal design of constant-stress and step-stress accelerated life tests. Reliability Engineering and System Safety, Vol. 140, 2015, p. 1-14.
-
Chen Yunxia, Jing Hailong, Liao Xun, Kang Rui Methods to determine stress profile in ALT based on theoretical life models. Chinese Journal of Aeronautics, Vol. 28, Issue 3, 2015, p. 729-736.
-
Willis A. J. Design of a modified SPRT for pipeline leak detection. Computers and Chemical Engineering, Vol. 35, 2011, p. 127-131.
-
Kang Rui, Wang Wenyu, Ma Xiaobing, Chen Qinfeng System level accelerated demonstration tests design: approach and application. Reliability and Maintainability Symposium, Vol. 94, Issue 23, 2014, p. 1-6.
-
Om Prakash Yadav, Xing Zhuang Reliability demonstration test planning: a three dimensional consideration. Reliability Engineering and System Safety, Vol. 91, 2006, p. 882-893.
-
Milena Krasich Realistic reliability requirements for the stresses in use. Reliability and Maintainability Symposium, 2003, p. 13-16.
-
David Han, Debasis Kundu Inference for a step-stress model with competing risks for failure from the generalized exponential distribution under type-I censoring. IEEE Transactions on Reliability, Vol. 64, Issue 1, 2015, p. 31-43.
-
Rosmaini A., Shahrul K., Ishak A. A., Indra P. A. Failure analysis of machinery component by considering external factors and multiple failure modes – a case study in the processing industry. Engineering Failure Analysis, Vol. 25, 2012, p. 182-192.
-
Giardina M., Castiglia F., Tomarchio E. Risk assessment of component failure modes and human errors using a new FMECA approach: application in the safety analysis of HDR brachytherapy. Journal of Radiological Protection; Vol. 34, 2014, p. 891-914.
-
Reliability Qualification Test and Reliability Acceptance Test. GJB899A, 2009.
-
Application Specific Qualification Using Knowledge Based on Test Methodology. JESD94A, 2008.
-
Luis Escobar A., William Meeker Q. A review of accelerated test models. Statistical Science, Vol. 21, Issue 4, 2006, p. 552-577.
-
Reliability Methodology for Electronic Systems. FIDES Guide 2009 Edition A.
-
Methods for Product Accelerated Testing. Edition 1, IEC 62506, 2013.
-
Ditlevsen O. Narrow reliability bounds for structural system. Journal of Structural Mechanics, Vol. 7, Issue 4, 1979, p. 453-472.
About this article
This work is supported by the National Natural Science Foundation of China (No. 61703391), and Technology and Engineering Center for Space Utilization (No. CSU-QZKT201714)
