Abstract
At present, the control of vibration problem of many engineering equipment can be simplified as a study on transverse vibration of axially traveling string system. In this paper, transverse vibration control and energy dissipation of axially traveling string system is investigated by using a boundary viscous damper. By analyzing the nature frequencies of the fixed length and the variable length of the string system, the resonance frequency of the external concentrated force is obtained. The amplitude and the energy reflection ratio of reflected wave to incident wave is investigated respectively by the force equilibrium principle and the energy equation at the boundary. According to amplitude and the energy reflection ratio, the range and the optimal value of damping coefficient are obtained. The effect of vibration dissipation with a viscous damper and an external concentrated force at the left boundary is investigated respectively by the numerical simulation.
1. Introduction
In the present paper, the transverse control study of axially traveling string system using the nature frequency, the boundary force equilibrium principle and the energy equation. This model can be used to study the transverse vibration problems of engineering equipment, such as conveyor belt, band-saws, tape, elevator, tethered satellite, etc. The vibration control of axially traveling string systems have been studied for many years, it is though still of great research interest due to their theoretical importance and application. For instance, Chung [1] and Tan [2] researched an exact, closed-form expression for the transverse response of the controlled system, consisting of the flexible structure, the wave controller, and the sensing and actuating devices, was derived in the frequency domain, the feedback controller and the active control law were established by employing the idea of wave cancellation showed effectively. The vibration characteristics of the traveling string with the free support of both ends, Ram [3] found that the high frequency vibration problem occurs when the string boundary was fixed. Shahruz [4] studied the nonlinear control and the vibration of the axially traveling string with the reflected speed at the boundary, but its boundary control is the negative feedback of the transversal velocity of the string at one end. The natural frequencies and vibrations control of a fixed-length string system have been studied extensively, and the study of the variable length string was extended. Galerkin’s procedure with a time-dependent basis function was used to obtain a discrete system, the natural frequencies of the string tend to decrease, while the unstable regions are shifted toward the lower frequency direction with increasing string length was researched by Fung [5]. And Chen [6] found that the stiffness in the load system tends to increase the natural frequencies of the traveling string, while the inertia tends to decrease the natural frequencies. The energy and stability of axially traveling string system with varying length were studied, and the factors that affect the stability of the system were analyzed by Zhu [7, 8]. Based on the characteristics of wave propagation, the nature frequencies and energy about its vibration were studied by Lee [9, 10], when the string length is varied, the natural frequencies and vibration energy were not constant. String tension and nonzero instantaneous transverse velocity at the moving boundary results in energy variation. Based on the Hamilton’s principle, an active vibration control and an adaptive boundary control in the right end of the axially traveling string were investigated by Chang [11] and Ngo [12]. The variable length transverse displacement response and energy problem were studied through the Hamilton's principle, and Sandilo [13] showed that the Galerkin’s truncation method cannot be applied in all cases to obtain approximations valid on long timescales. Chen [14] used the Lagrange equation and finite element method to establish the model of an axially traveling string system with a damper at one end, investigated the problem of its free vibration response and energy dissipation.
In contrast to the previous work on the vibration control of axially traveling string system based on energy change and boundary feedback which requires many complex calculations, the present work focuses on using the characteristics of wave propagation to study the boundary damping control and to analyze the natural frequencies of the string system can effectively simplify the calculation process and the result is obvious. Then the factors for the variation of the amplitudes and the energy of the string vibration are analyzed after calculating the amplitude ratio and the energy ratio of the incident wave to the reflected wave, as well as the natural frequencies of the string system. The optimal value of the boundary damping coefficient is obtained in this work. This paper is organized as follows. Section 2 introduces the vibration model of a travelling string with variable length and a viscous damper at its left end. In Section 3, we use the characteristics of traveling wave to obtain two opposite direction waves and calculate the natural frequencies of the string system with constant or variable length. In Section 4, according to the boundary force equilibrium principle, the ranges of the damping coefficient in which the vibration of the string is reduced are obtained and the optimal value of the damping coefficient is given analytically. Then numerical simulations are presented to prove the effectiveness of the proposed method. Section 5 provides the main conclusions finally.
2. The model of axially traveling string
The model shown in Fig. 1 is an axially traveling string with variable length and a various damper at its left end, which is established based on the following assumptions: the line density and tension remain constant during the motion; the longitudinal vibration is neglected and the elastic deformation caused by transverse vibration is smaller than the length of axially traveling string.
Fig. 1Simplified model of axially travelling string system with damping device
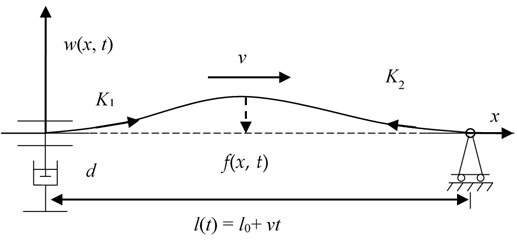
In Fig. 1, is the transverse displacement of the string at time and at position , is the initial string length, is the string length at time and is the velocity of traveling string. Here, two cases concerning the string length are considered: one is the constant length case, i.e. and so ; the other is the linearly changing length case, i.e. , and so . is damping coefficient of the viscous damper, is the external concentrated force, and are the traveling waves to the left end and to the right end of the string respectively.
The motion equation of a travelling string will be obtained by applying the Hamilton’s principle in the following form [15]:
where is a variation in a function, is the virtual energy, is the Lagrangian function which requires the kinetic energy and the potential energy given by:
where, and are the first order partial derivative of with respect to and , respectively. The virtual energy has the following form:
where, is the damping force which is . Substituting Eqs. (2), (3) and (4) into Eq. (1), one can obtain:
Taking the variation with respect to and in Eq. (5), the expression becomes:
According to Hamilton’s principle, the time end conditions are satisfied, i.e.:
Applying integration by parts to the two terms in the integral in the Eq. (6) and Eq. (7), one can obtain:
where, is the second order partial derivative of with respect to time , is the second order partial derivative of with respect to x and respectively and is the second order partial derivative of with respect to .
Since the variation over the interval is arbitrary, Eq. (8) can be satisfied only when the individual terms of Eq. (8) are equal to zero:
Eq. (9) represents the boundary condition while Eq. (10) denotes the equation of motion. Substituting the free wave propagation speed:
Into Eq. (10), one can obtain the equation of motion:
3. Natural frequencies of travelling string
A one-dimensional travelling wave is in the form [16, 17]:
where, is the amplitude, is angular frequency and is the wave number.
Based on the characteristics of traveling wave, the traveling wave solution can be represented by two independent traveling waves:
where, , are the amplitude and wave number of the incident wave ; , are the amplitude and wave number of the reflected wave . Substituting the one-dimensional travelling harmonic wave Eq. (13) into the wave Eq. (12) yields the values of the wave numbers and as follows:
According to [18], we obtain the wave number:
where, represent the modal order of the string system. The wavelength in the th mode of the string is:
Then the relationship between the string length and wavelength in the axially moving string system can be obtained by Eq. (17) and (18). Fig. 2 shows the first 4 modes of a string:
Assuming that: it takes time for the wave to travel from 0 to and time for the wave to return to 0. Then the motion cycle corresponding to the -order natural mode is:
Fig. 2Relationship between wavelengths and length of axially travelling string
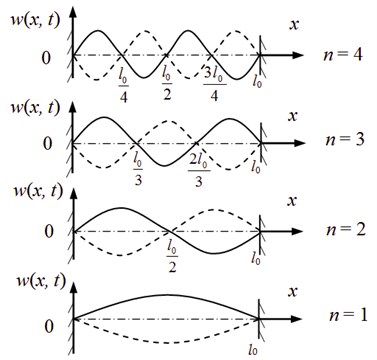
3.1. Constant length string
In the case of constant length string, we have . When the travelling speed 0, , then the -order motion cycle is:
According to the relationship between the motion cycle and the natural frequencies, the nature frequencies is obtained as follows:
Similarly, when , one has:
Substituting Eqs. (23), (24) into Eq. (20), the -order vibration cycle and nature frequencies are:
3.2. Variable length string
In the case of variable length string, we have , that the length of the string changes linearly. When the wave moves from 0 to the boundary , where is the time it takes in this duration, one has the following equation:
From Eq. (27), the time is obtained:
When the wave is reflected at the boundary and moves back to the other boundary 0, the time it takes in this duration and length of the string at the time are as follows:
Then the first motion cycle is:
Repeating the same process, one can obtain the th motion cycle and its nature frequencies , which are:
4. Boundary damping vibration control
4.1. Amplitude attenuation
As shown in Fig. 1, the viscous damper is added at the boundary ( 0) and the force equilibrium principle in the transverse direction at the end point ( 0) of the string is obtained as follow:
where:
By substituting Eqs. (35) and (36) into Eq. (34), one can obtain the amplitude ratio of reflected wave and incident wave:
In order to analyze the influence of the damping coefficient on amplitude ratio , we take a derivative of with respect to with the assumption that the tension , the mass density and the velocity remain constants and we have:
From Eq. (38), the reflected wave amplitude at the left end ( 0) decreases with the increasing of damping coefficient . Furthermore, in order to inhibit the vibration, the amplitude ratio of is needed to satisfy:
According to Eqs. (37) and (39), we can obtain the range of damping coefficient of the damper at 0 which can attenuate the amplitude of vibration effectively:
4.2. Energy dissipation
To study the energy dissipation for the viscous damper set at one end of the string ( 0), the explicit expressions for the energy contained in one wavelength of the incident wave and the effected wave in the end with a damper are studied. Firstly, we give the energy contained in one wavelength for a one-dimensional traveling harmonic wave . Since the time is arbitrary, we select 0, then the energy expression is:
where:
Substituting the imaginary parts of Eqs. (42) and (43) into Eq. (41), one has:
Remark that , the integration can easily be obtained by using variable substitution yielding:
Substituting Eqs. (45), (11) and (16) into Eq. (44), we have the energy expression finally:
Then substituting Eqs. (15) and (16) into Eq. (46) respectively, one can obtain the expressions of energy for the incident wave and the reflected wave as follows:
Here, we can obtain the energy ratio of the incident wave and the reflected wave as follows:
In order to dissipate the vibration energy by the damper effectively, the energy ratio will satisfy the condition as follows:
By substituting Eq. (49) into Eq. (50), we obtain the range of the boundary damping coefficient:
4.3. Scope of boundary damping coefficient and the optimal value
In this subsection, we consider the scope of boundary damping coefficient. The amplitude ratio and the energy ratio of reflected wave and the incident wave in axially moving string system should satisfy both Eqs. (39) and (50). Incorporate the conditions given by Eqs. (40) and (51), note that:
Then we obtain the range of boundary damping coefficient for energy dissipation as follows:
Here, is the critical value of when 1 and . When the damping coefficient is within the scope of Eq. (40), the damper can reduce transverse vibration of the axially moving string. When no energy is reflected from the end of the string with damper, that is:
It means that all the incident energy is dissipated by the damper completely, the viscous damping coefficient should satisfy Eq. (54). Substituting Eqs. (37) and (49) into Eq. (54), the optimal value of damper can be obtained:
The optimal value of damper in this paper is consistent with the one in [16] using the definition of mechanical impedance, whose result is that the optimal value of damper is equal to the downstream impedance, which has the value of when the damper is placed at the right end of the string, i.e. . In this paper, the damper is placed at the left end of the string, i.e. 0, so the optimal value of damper is equal to the upstream impedance, i.e. , accordings to the results in [16].
4.4. Numerical simulation and analysis
Consider an initial condition chosen to be:
The parameters of axially travelling string system are selected as follows: the initial string length is 18 m, the initial displacement amplitude of string is 0.01 m and the mass density of string in mass per unit length is 0.01 kg/m. To study the amplitude ratio and the energy ratio between different working conditions, which have different parameters, 16 sets of parameters for tension , mass density and traveling speed v are given in Table 1. According to Eqs. (37) and (49) and using the 16 sets parameters, we can obtain the amplitude ratio and the energy ratio of transverse wave for constant length string, which are shown in Fig. 3 to Fig. 6.
Table 1Parameters of axially travelling string system
/ (N) | / (kg/m) | / (m/s) | |||
10 | 0.01 | 0 | –2 | –4 | –6 |
10 | 0.01 | 0 | 2 | 4 | 6 |
20 | 0.01 | 0 | –2 | –4 | –6 |
20 | 0.01 | 0 | 2 | 4 | 6 |
Fig. 3 to Fig. 7 show that the amplitude ratio and energy ratio for the damping boundary at 0 with different tensions and traveling speeds v given in Table 1. Some points will be discussed as follows:
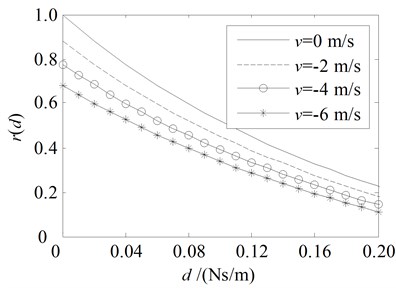
It is clear that the amplitude ratio decreases monotonically with the increase of damping coefficient while the energy ratio has a minimum value, i.e. 0 when is equal to the optimal value .
When the traveling speed v is negative value, namely the string traveling upstream, one can see from Fig. 3(a), Fig. 5(a) and Fig. 7(a) that, the amplitude ratio and the energy ratio are always less than 1 even no damping, i.e. 0. It means that the energy is reduced for the traveling wave reflected at the upstream end ( 0) when the string travels upstream () even no damping due to the negative work done by the fixed boundary.
When the traveling speed v is positive value, namely the string traveling downstream, one can see from Fig. 4(a), Fig. 6(a) and Fig.7(b) that, the amplitude ratio and the energy ratio are always large than 1 when 0, i.e. no damping at the upstream end. It means that the energy will increase for the traveling wave reflected at the upstream end ( 0) without damping when the string travels downstream () due to the positive work done by the fixed boundary.
The theoretical values for the optimal damping coefficient and the critical damping coefficient list in Table 2 are agree well with the values in the curves shown in Figs. 3-6, which proves the accuracy of this method.
Comparing Fig. 3(b) with Fig. 4(b), one can see that the optimal value decreases with the increase of when while increases with the increase of when . It is clear that a downstream traveling string with higher speed need more damping force to reduce the energy while an upstream traveling string with higher speed need less damping force to reduce the energy. This suggests that we should install the damper at the downstream end of the string to reduce its vibration effectively.
Comparing Fig. 4(b) with Fig. 6(b), one can see that with the increase of tension , the optimal damping coefficient increases, which is agree with Eq. (55).
Table 2The values of dopt and dcri corresponding to Table 1
(Ns/m) | (Ns/m) | ||||||
0.32 | 0.30 | 0.28 | 0.27 | × | × | × | × |
0.32 | 0.34 | 0.36 | 0.39 | × | 0.02 | 0.04 | 0.06 |
0.45 | 0.43 | 0.41 | 0.39 | × | × | × | × |
0.45 | 0.47 | 0.49 | 0.52 | × | 0.02 | 0.04 | 0.06 |
Fig. 3Amplitude ratio rd and energy ratio Rd for the damping boundary at x= 0 with the parameters in the first line in Table 1
a) Amplitude ratio
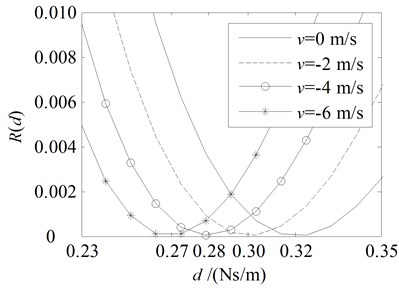
b) Energy ratio
Fig. 4Amplitude ratio rd and energy ratio Rd for the damping boundary at x= 0 with the parameters in the second line in Table 1
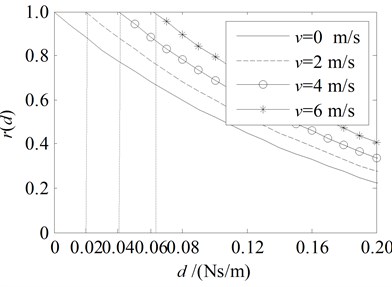
a) Amplitude ratio
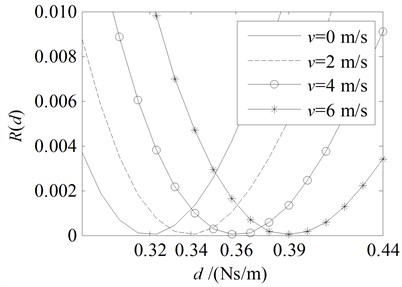
b) Energy ratio
Fig. 5Amplitude ratio rd and energy ratio Rd for the damping boundary at x= 0 with the parameters in the third line in Table 1
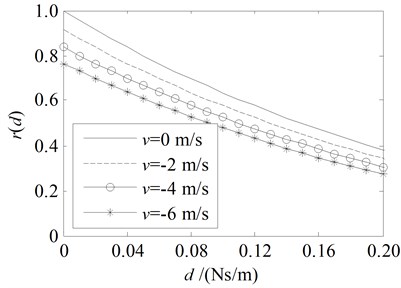
a) Amplitude ratio
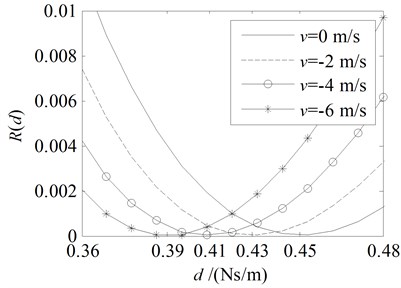
b) Energy ratio
Fig. 6Amplitude ratio rd and energy ratio Rd for the damping boundary at x= 0 with the parameters in the 4th line in Table 1
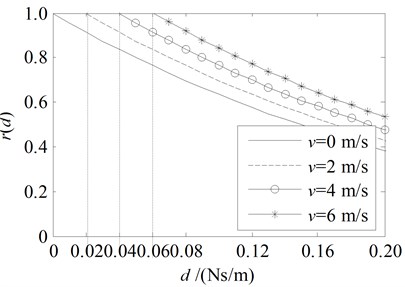
a) Amplitude ratio
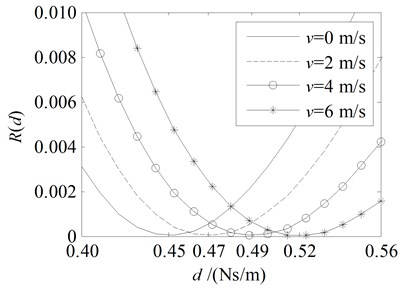
b) Energy ratio
Fig. 7Energy ratio Rd for the damping boundary at x= 0 with the parameters in the third line and the 4th line in Table 1
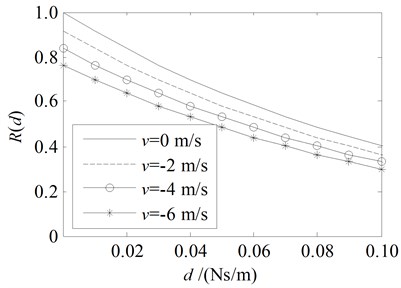
a)
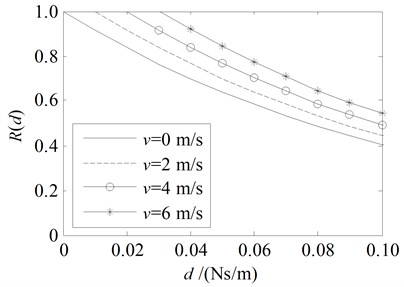
b)
In order to study the change of total energy of a string with different damping, velocity and tension, some numerical examples are given below. The free vibration of the string is carried out due to the initial condition given by Eq. (56). The parameters are selected in Table 3, so we can obtain the total energy by using Eq. (41) with variable damping coefficient. Then we can know whether the transverse vibration of the string system can be effectively controlled by the boundary damping. is the initial system energy.
Table 3Parameters of variable damping coefficients (x= 0)
/ (N) | / (m/s) | / (kg/m) | / (Ns/m) | ||||
10 | 0 | 0.01 | 5.0 | 1.0 | 0.32 (optimal value) | 0.10 | 5.5 |
20 | 0 | 0.01 | 5.0 | 1.0 | 0.45 (optimal value) | 0.10 | 7.8 |
10 | –2.0 | 0.01 | 5.0 | 1.0 | 0.30 (optimal value) | 0.10 | 5.5 |
10 | 2.0 | 0.01 | 5.0 | 1.0 | 0.34 (optimal value) | 0.10 | 5.5 |
Fig. 8The total energy change with variable damping coefficient
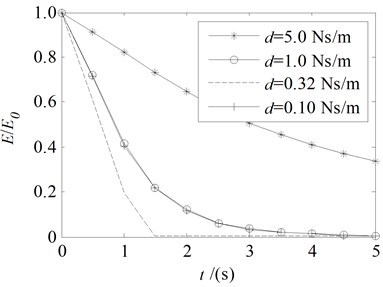
a) 10 N, 0 m/s, 0.32 Ns/m
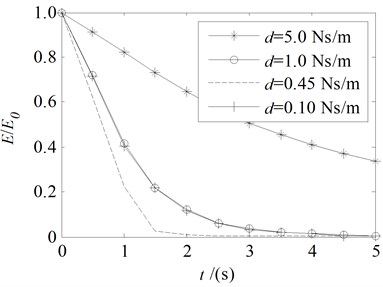
b) 20 N, 0 m/s, 0.45 Ns/m
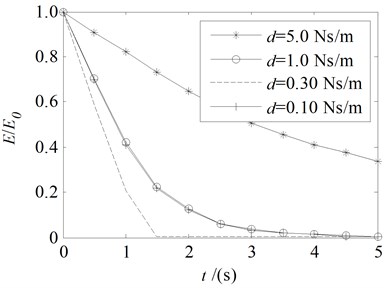
c) 10 N, –2.0 m/s, 0.30 Ns/m
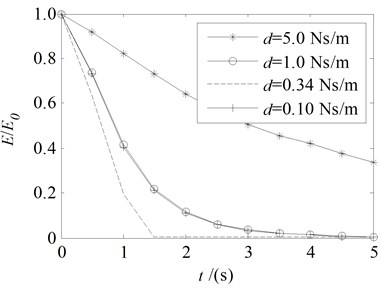
d) 10 N, 2.0 m/s, 0.34 Ns/m
In Fig. 8, one can see that the dissipation of energy is larger with the increase of tension , but it has a little impact with the positive and negative of . The system energy can be effectively dissipated by the boundary damping. Compared to be other values of damping coefficient, the energy is rapidly reduced to zero when the damping coefficient is the optimum value.
In the above, the analysis of the energy dissipation is based on the boundary damping control. Now, we add an external concentrated force at the midpoint of the string, , where is chosen to be the first order natural frequencies given by Eq. (26). The transverse vibration displacement responses at midpoint for fixed length string are considered and obtained as follows according to the parameters in Table 3.
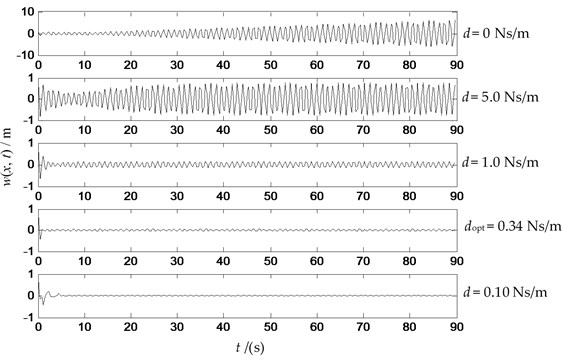
From the Figs. 9-12, one can see that: when there is no damping, resonance is caused by external concentrated force f at the midpoint whose frequency is equal to the first order nature frequencies of the string system. The damping set at the upstream end of the string with the given damping values within the scope defined by Eq. (53) can effectively inhibit the transverse vibration displacement. The vibration energy is dissipated obviously when the boundary damping coefficient is equal to the optimum value.
Fig. 9The transverse vibration displacements at the midpoint with variable damping (P= 10 N, v= 0 m/s, f= sin (5.5 t)) N
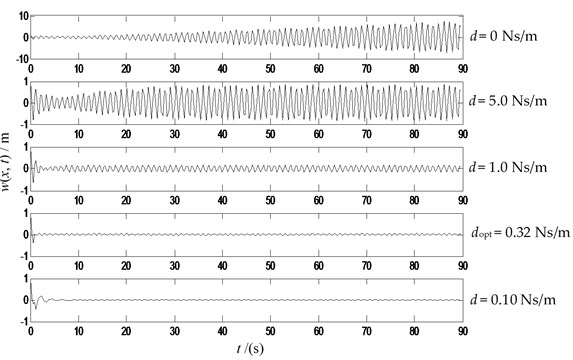
Fig. 10The transverse vibration displacements at the midpoint with damping (P= 20 N, v= 0 m/s, f= sin (7.8 t)) N
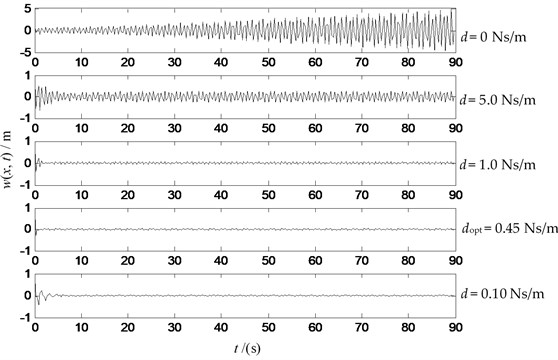
Fig. 11The transverse vibration displacements at the midpoint with variable damping (P= 10 N, v= –2 m/s, f= sin (5.5 t)) N
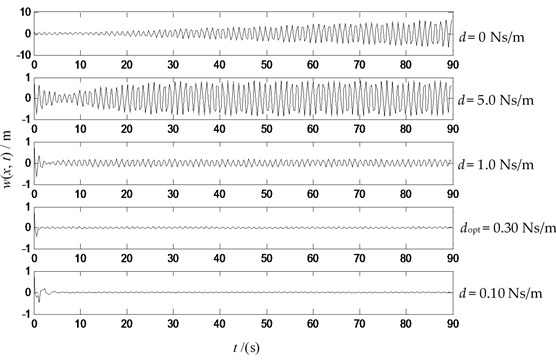
Fig. 12The transverse vibration displacements at the midpoint with variable damping (P= 10 N, v= 2 m/s, f= sin (5.5 t)) N
5. Conclusions
1) Based on Hamilton principle and Lagrangian function, a model of axially traveling string is built and the natural frequencies of a traveling string with constant and variable length is given analytically using the reflection of wave propagation at the boundary of a string.
2) The amplitude ratio and the energy ratio of the reflected wave to the incident wave based on the force equilibrium principle for a damping set at the upstream end of a traveling string. The scope of the damping coefficient for the vibration dissipation is obtained and the optimal value for no energy is reflected at the damping boundary is given analytically.
3) Numerical examples for a boundary damping traveling string system with free vibration and forced vibration by external concentrated force are studied and the theories proposed are proved, which can provide some theoretical support for the actual project about transverse vibration control of string system.
References
-
Chung C. H., Tan C. A. Active vibration control of the axially traveling string by wave cancellation. Journal of Vibration and Acoustics, Vol. 117, Issue 1, 1995, p. 49-55.
-
Tan C. A., Ying S. Active wave control of the axially traveling string: theory and experiment. Journal of Sound and Vibration, Vol. 236, Issue 5, 2000, p. 861-880.
-
Ram Y. M., Caldwell J. C. The free vibration of a string with traveling boundary conditions by the method of distorted images. Journal of Sound and Vibration, Vol. 194, Issue 1, 1996, p. 35-47.
-
Shahruz S. M., Kurmaji D. A. Vibration suppression of a non-linear axially traveling string by boundary control. Journal of Sound and Vibration, Vol. 201, Issue 1, 1997, p. 145-152.
-
Fung R. F., Chu J. J., Huang J. S. Dynamic stability of an axially travelling string/slider coupling system with traveling boundary. Journal of Sound and Vibration, Vol. 211, Issue 1, 1998, p. 689-701.
-
Chen J. S. Natural frequencies and stability of an axially-traveling string in contact with a stationary load system. Journal of Vibration and Acoustics. Vol. 119, Issue 2, 1997, p. 152-157.
-
Zhu W. D., Ni J. Energetics and stability of translating media with an arbitrarily varying length. Journal of Vibration and Acoustics, Vol. 122, Issue 3, 2000, p. 295-304.
-
Zhu W. D., Ni J., Huang J. Active control of translating media with arbitrarily varying length. Journal of Vibration and Acoustics, Vol. 123, Issue 3, 2001, p. 347-358.
-
Lee S. Y., Lee M. A new wave technique for free vibration of a string with-varying length. Journal of Applied Mechanics, Vol. 69, Issue 1, 2002, p. 83-87.
-
Lee S. Y., Jr C. D. M. Vibration control of an axially traveling string by boundary control. Journal of Dynamic Systems, Measurement, and Control, Vol. 118, Issue 1, 1996, p. 66-74.
-
Chang W. K., Hong K. S., Park H. Boundary control of an axially traveling string: Actuator Dynamics Included. Journal of Mechanical Science and Technology, Vol. 19, Issue 1, 2005, p. 40-50.
-
Ngo Q. H., Hong K. S., Jung I. H. Adaptive control of an axially moving system. Journal of Mechanical Science and Technology, Vol. 23, Issue 11, 2009, p. 3071-3078.
-
Sandilo S. H., Horssen W. T. V. On variable length induced vibrations of a vertical string. Journal of Sound and Vibration, Vol. 333, Issue 11, 2014, p. 2432-2449.
-
Chen E. W., Ferguson N. S. Analysis of energy dissipation in an elastic traveling string with a viscous damper at one end. Journal of Sound and Vibration, Vol. 333, Issue 9, 2014, p. 2556-2570.
-
Gaiko N. V., Horssen W. T. V. On the transverse, low frequency vibrations of a traveling string with boundary damping. Journal of Vibration and Acoustics, Vol. 137, Issue 4, 2015, https://doi.org/10.1115/1.4029690.
-
Lee S. Y., Jr C. D. M. A generalized treatment of the energetics of translating continua, part I: strings and second order tensioned pipes. Journal of Sound and Vibration, Vol. 204, Issue 5, 1997, p. 717-734.
-
Lee S. Y., Jr C. D. M. Traveling wave dynamics in a translating string coupled to stationary constraints: energy transfer and more localization. Journal of Sound and Vibration, Vol. 212, Issue 1, 1998, p. 1-22.
-
Singiresu S. R. Mechanical Vibrations. 4th Edition, Prentice Hall, U.S.A, 2004.
Cited by
About this article
The authors are greatly indebted to the National Natural Science Foundation of China (Grant No. 51675150 and Grant No. 51305115) for the support of this research.
Enwei Chen and Jun Wang worked on the theory derivation of natural frequencies and boundary damping control; Jun Wang and Kai Zhong were in charge of programming; Yimin Lu and Haozheng Wei analyzed the data; finally, Enwei Chen wrote the paper.
