Abstract
Sand-rubber mixtures has characteristics of light weight, cheap and environmental-friendly, thereby it has a great potential to be used in geotechnical engineering for sustainable development. Dynamic properties (i.e. shear modulus and damping ratio) of sand-rubber mixtures in a small range of shearing strain amplitudes (i.e. 10-6-10-4) were investigated in this study through a series of resonant column tests. The effects of shearing strain amplitude, confining pressure and rubber content on dynamic shear modulus (), maximum dynamic shear modulus (), damping ratio () and dynamic shear modulus ratio of the mixtures were also discussed. Based on the analyses of the relationship among confining pressure, rubber content and , an empirical formula for predicting considering the effects of confining pressure and rubber content was also proposed. The model prediction agreed with the experimental results very well.
1. Introduction
With a rapid development of national economy, the number of cars is increased considerably, which leads to the proliferation of waste tires and other rubber byproducts. As reported [1], the annual output of tire in the world is up to 9 million tons. The need of recycling waste automobile tires for environmental protection lead civil engineering research community on contriving ways to reuse these materials in an innovative manner [2]. Recycled rubber tires or mixed with granular soils have been used as backfill, drainage or thermal-isolation materials in the last several years for geotechnical applications [3]. Recycled tires in granulated or shredded form exhibit frictional behavior, low unit weight of solids, low bulk density, and high elastic deformability [4].
Sand is raw material, and rubber shred is considered as light material in sand-rubber mixtures. It has the advantages of light weight, high strength, high permeability, short construction period, waste recycling and environmental protection, resulting in a wide range of application in foundation engineering in developing countries particularly for earthquake protection [5]. The mixtures works as a cushion between the subgrade soils and foundation (as shown in Fig. 1(a)). Thus, it is very essential to study dynamic properties of this material. Evidences have already been shown in the simulations presented in the form of Fourier Amplitude Spectra (FAS) in Figs. 1(a) and (b), from which significant reduction in amplitudes could be observed in high-frequency range. It is therefore believed that seismic isolation using rubber-soil mixture (RSM) should be a feasible method, considering the excellent energy absorption capability of rubber.
Mixtures of soils with relatively low to medium rubber content (< 35 % per weight or < 55 % per volume) exhibit a reduction of void ratio with the increasing rubber content, that is a denser fabric of the soil-rubber solid matrix with relatively high shear strength and low to medium compressibility [6, 7].
Fig. 1a) Schematic drawing of the proposed seismic isolation method using a layer of rubber-soil mixture (RSM) – the cushion [5], b) The Fourier Amplitude Spectra (FAS) of the horizontal and vertical ground accelerations; and the corresponding normalised horizontal and vertical ground acceleration time histories for the Reference scenario. [5]
![a) Schematic drawing of the proposed seismic isolation method using a layer of rubber-soil mixture (RSM) – the cushion [5], b) The Fourier Amplitude Spectra (FAS) of the horizontal and vertical ground accelerations; and the corresponding normalised horizontal and vertical ground acceleration time histories for the Reference scenario. [5]](https://static-01.extrica.com/articles/18279/18279-img1.jpg)
a)
![a) Schematic drawing of the proposed seismic isolation method using a layer of rubber-soil mixture (RSM) – the cushion [5], b) The Fourier Amplitude Spectra (FAS) of the horizontal and vertical ground accelerations; and the corresponding normalised horizontal and vertical ground acceleration time histories for the Reference scenario. [5]](https://static-01.extrica.com/articles/18279/18279-img2.jpg)
b)
Work related to the dynamic properties of sand-rubber mixtures had been reported in literatures. For example, Feng and Suttter [8] and Anastasiadis et al. [9] investigated shear modulus and damping ratio of granulated rubber/sand mixtures using torsional resonant column tests. Nakhaei et al. [10] conducted large-scale consolidated undrained cyclic triaxial tests on granular soils mixed with granulated rubber. The effects of rubber content and confining pressure on dynamic properties of mixtures were also assessed. Moreover, Nakhaee and Marandi [11] also studied the dynamic properties of rubber-soil mixtures, and its application in making slopes behind retaining wall. It is indicated that the earth pressure acting on the wall caused by earthquake can be significantly reduced using rubber-soil mixtures. In addition, Zhong et al. [12] studied the potential application of rubber-modified asphalt in railroad track beds by measuring its shear modulus and damping ratio. Christ et al. [13] addressed the potential use of granulated rubber-sand as backfill material for buried pipelines in cold regions. In order to solve the environmental problem caused by the discarded waste tire rubber, dynamic properties of sand-rubber mixtures (i.e. dynamic shear modulus and damping ratio) in a small range of shearing strain amplitudes (10-6-10-4) was studied by resonant column test in this study. The effects of shear strain amplitude, confining pressure and rubber content on the maximum dynamic shear modulus (), damping ratio and dynamic shear modulus ratio () of the sand-rubber mixtures were discussed. In addition, based on the analyses of the relationship between confining pressure, rubber content and , an empirical formula for predicting considering the effects of confining pressure and rubber content was proposed. The dynamic shear modulus ratio , the relationship between the damping ratio and the shearing strain of the mixtures were obtained as well.
2. Materials and methods
2.1. Materials
A silica sand and tire shred were selected to perform laboratory tests in this study. Material properties and photos of sand and rubber shred are shown in Table 1. The particle size distribution curves of sand and rubber shred are shown in Fig. 2. According to ASTM D2487 [14], the sand is classified as poorly graded sand (SP) with a median grain size () of 0.30 mm, and a specific gravity () of 2.64. The rubber shred is made of crushed waste tire, with a median grain size () of 1.52 mm, and specific gravity () of 1.15 which is much less than that of the sand.
Table 1Material properties of sand and rubber shred
Property | Sand | Rubber shred |
2.64 | 1.15 | |
(mm) | 0.30 | 1.52 |
0.88 | – | |
0.62 | – | |
(g/cm3) | 1.60 | 0.52 |
2.50 | 1.91 | |
1.11 | 1.05 | |
Photo |  |  |
2.2. Sample preparation
In the experiments, sand-rubber mixtures were prepared according to the following procedures: (1) Dry sand and rubber shred were first thoroughly mixed in certain proportions with rubber content ranging from 0 %, 5 %, 10 %, 15 % to 20 % by dry weight; (2) Dry mixture was then mixed with predetermined weight of water thoroughly. The target degree of saturation of specimen was 0.97; (3) The mixture was compacted in five equal layers in a mold of a height of 80 mm and an inner diameter of 39.1 mm. The schematic of sample preparation is shown in Fig. 3; (4) The mold was then separated, and the completed sand-rubber mixture sample with different rubber contents is shown in Fig. 4.
Fig. 2Particle size distribution curves of sand and rubber
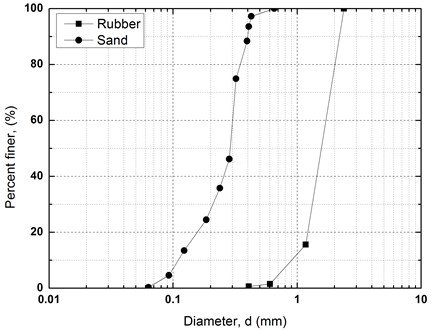
Fig. 3Schematic of sample preparation
Fig. 4Photo of sand-rubber mixture samples with different rubber contents (Note: R refers to rubber content)

0 %

5 %

10 %

15 %

20 %
2.3. Experimental setup
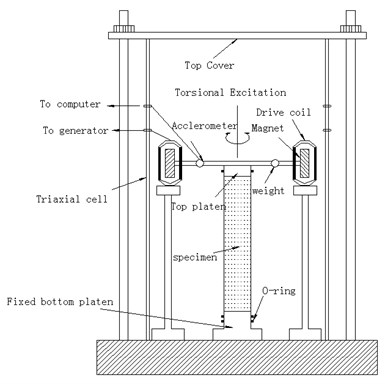
The experimental setup, i.e. GZZ-50-type resonant column instrument, used in this study is shown in Fig. 5(a) and (b). In the experiments, confining pressures were set as 100 kPa, 200 kPa, 300 kPa and 400 kPa, respectively. At each confining pressure, the excitation force was increased gradually during the test. The acceleration and self-vibration frequency of self-vibration at all levels of pressure were measured by the computer. The whole test process is generally divided into twelve steps regarding the excitation process. The attenuation waveform is displayed after each afterburner for observation by the experimenter. Once the previous vibration test is completed, the computer automatically increases the torque by a specified multiple (about 1.3 times) until twelve loads are finished. When the shear strain reaches 5×10-4, the test is stopped automatically.
Fig. 5Sketch and photo of resonant column experimental setup
a)

b)
3. Results and discussion
3.1. Dynamic shear modulus ()
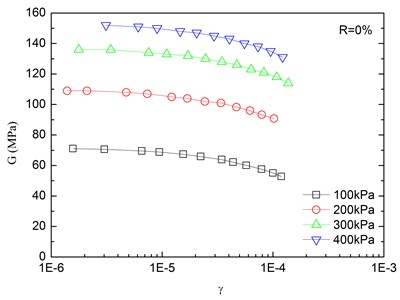
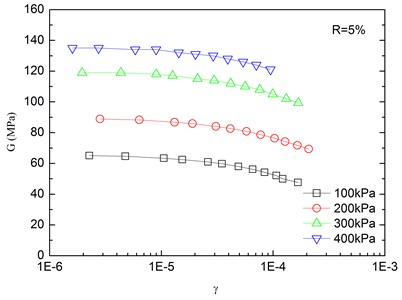
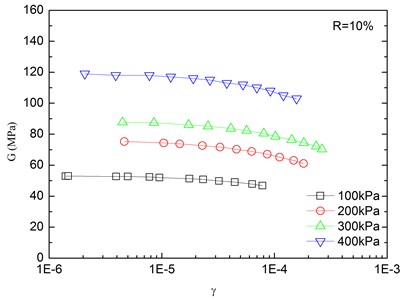
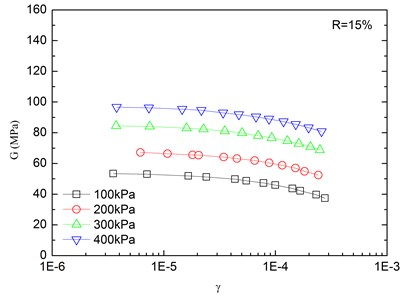
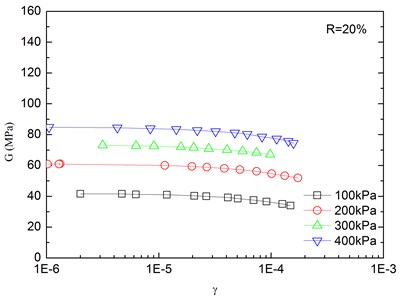
The relationships between the dynamic shear modulus () and the shear strain () of sand-rubber mixtures under different confining pressures are shown in Fig. 6. The rubber content is ranged from 0 %, 5 %, 10 %, 15 % and 20 %. It is indicated that the - relationships of the mixtures exhibited non-linear characteristics when the shear strain exceeded 10–5, regardless of the rubber content and level of the confining pressure. It is also found that the shapes of the - curves of the mixtures were similar for different rubber contents. With an increase in shear strain, the dynamic shear modulus tended to be decreased. When the shear strain was in the range of 10-5-10-4 (i.e. dynamic elastic deformation regime), the dynamic shear modulus decreased with an increase in the dynamic shear strain. When the shear strain was greater than 10-4, the increase of the shear strain led to the greater the rate of attenuation of the dynamic shear modulus.
The effect of confining pressure on dynamic shear modulus was also investigated as shown in Fig. 6. At the same shear strain level, a larger confining pressure led to a larger dynamic shear modulus. It is because that the increase of confining pressure reduces the void ratio of sand-rubber mixtures, and increases amount of inter-particle physical contact points and relative density of the mixtures. As a result, the mixture become denser, and the dynamic shear modulus is increased. Due to the relatively high elastic modulus of the rubber, the increase of volume fraction of rubber particles reduces the nonlinear characteristic of the - curves of the mixtures. It is also found that the dynamic shear modulus of mixtures with 20 % rubber content was almost linearly varied with the shear strain.
Fig. 7 presents relationships between dynamic shear modulus and shear strain at varying rubber contents. Under the same shear strain condition, the increase of rubber content reduced the dynamic shear modulus of the sand-rubber mixtures, so it can be used for vibration isolation. Additionally, the dynamic shear modulus curve tended to be gradually varied with shear strain, which is mainly because the rubber particles are highly elastic material as compared to the sand. Moreover, the increase of rubber content leads to an increase of structure weak surface of the mixtures, and reduces the structure integrity. The strength of the mixtures is decreased as a result. On the other hand, the increase of rubber content also leads to a greater elasticity of the mixtures. The mechanical properties of the mixtures are gradually changed from more sand-like material to more rubber-like material.
Fig. 6Relationships between shear modulus and shear strain at varying confining pressures (Note: R refers to rubber content)
a)
b)
c)
d)
e)
3.2. Damping ratio
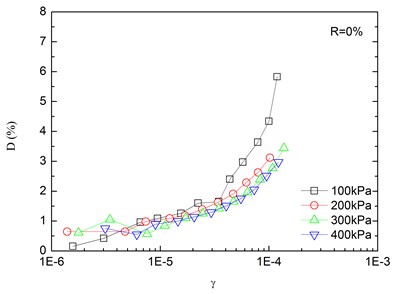
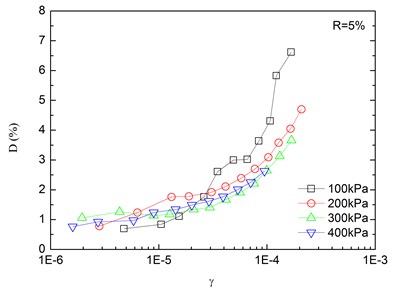
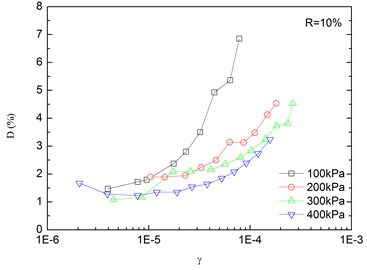
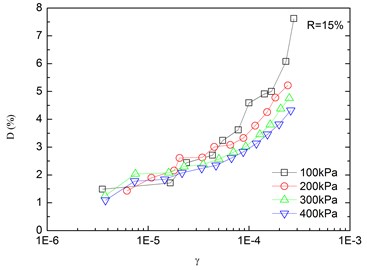
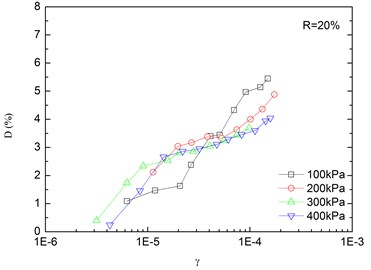
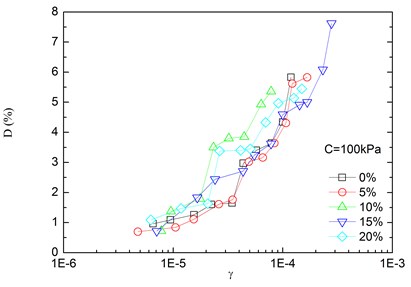
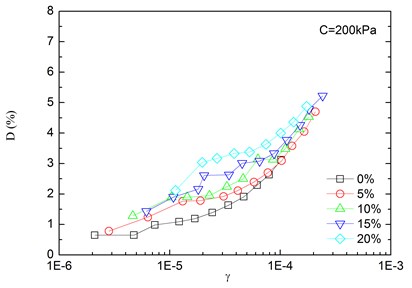
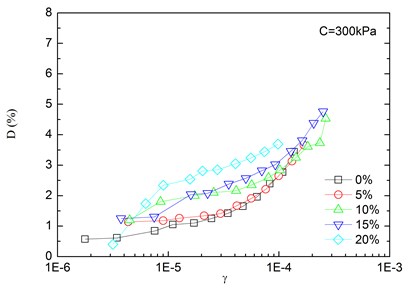
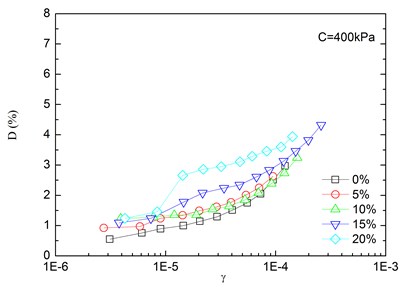
Variation of damping ratio of sand-rubber mixtures with shear strain was obtained in resonant column tests. Fig. 8 presents the relationships between damping ratio and shear strain at varying confining pressures. The damping ratio of the mixtures generally increased with the increase of shear strain. In addition, the obtained damping ratio under different confining pressures had a similar trend. When the shear strain was greater than 10-5, the damping ratio of the mixtures started to increase non-linearly and rapidly with the shear strain. It is also indicated that the effect of confining pressure on the damping ratio was not significant. It is because that the stress of the mixture is small when the strain is in a low range, thereby the change of damping ratio caused by the change of confining pressure is not prominent. However, it is observed that the damping ratio was tended to decrease slightly with increasing confining pressure. Similarly, Fig. 9 presents the relationships between damping ratio and shear strain at varying rubber contents. It is found that the increase of rubber content caused an increase in peak value of damping ratio of sand-rubber mixtures under the same confining pressure. Moreover, the increase of damping ratio was obvious when the shear strain was greater than 10-5.
Fig. 7Relationships between shear modulus and shear strain at varying rubber contents (Note: C refers to confining pressure)
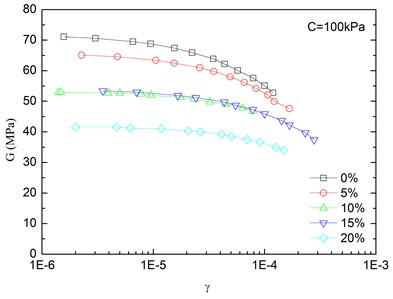
a)
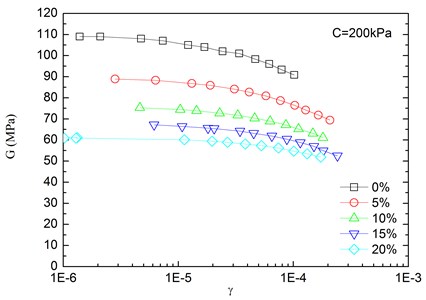
b)
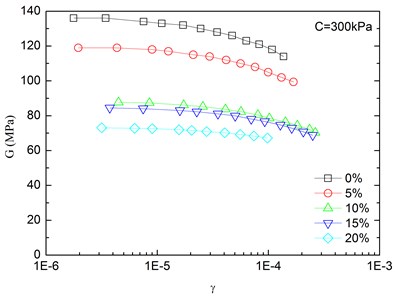
c)
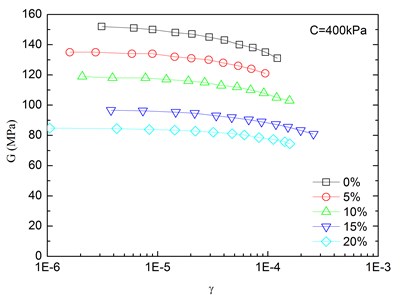
d)
3.3. Maximum shear modulus ()
The maximum dynamic shear modulus is one of the most important soil parameters for dynamic analyses and design in geotechnical engineering. When the soil deformation is in a relatively small range of shearing strain, the linear elastic properties of soils and the small strain behavior do not show hysteresis effect. It also reveals that the stress characteristics of soil is elastic, the process of no energy dissipation, deformation or shear deformation can be fully restored. The maximum dynamic shear modulus () is the shear modulus at which the shearing strain tends to be zero, and the shear modulus is the maximum dynamic shear modulus in a small range of shearing strain.
The ideal method to measure the maximum dynamic shear modulus of soils is to adopt the resonant column test method. The resonant column device can perform the test in a small range of shearing strain amplitude (i.e. 10-6-10-4) under different conditions of dynamic shear modulus. In addition, the effects of confining pressure and rubber content on the maximum dynamic shear modulus can be investigated as well.
Fig. 8Relationships between damping ratio and shear strain at varying confining pressures (Note: R refers to rubber content)
a)
b)
c)
d)
e)
Table 2Summary of calculated Gmax
Confining pressure (kPa) | Rubber content (%) | ||||
0 | 5 | 10 | 15 | 20 | |
100 | 80.36 | 67.66 | 51.59 | 46.55 | 36.38 |
200 | 116.64 | 89.59 | 82.44 | 63.69 | 59.14 |
300 | 148.39 | 113.32 | 102.36 | 83.94 | 72.37 |
400 | 167.59 | 137.08 | 110.19 | 91.76 | 81.46 |
According to the relationship between the reciprocal of the dynamic shear modulus and the hyperbolic model, the analytical calculation can be fitted according to the equation . When , , the maximum dynamic shear modulus can be calculated. Table 2 presents the calculated maximum dynamic shear modulus of sand-rubber mixtures with different rubber contents at different confining pressures.
Fig. 9Relationships between damping ratio and shear strain at varying rubber contents (Note: C refers to confining pressure)
a)
b)
c)
d)
Fig. 10 depicts the relationships between the maximum dynamic shear modulus () of the sand-rubber mixtures and confining pressure. It is found that the greater the confining pressure was, the higher the maximum dynamic shear modulus () of the mixtures was. This is because the elevated confining pressure causes more bonding among sand particles in mixtures, resulting in an increase of friction at the contact area among particles. It is also indicated that the increase of confining pressure increased the peak value of the maximum dynamic shear modulus () of the mixtures. Additionally, the maximum dynamic shear modulus () of the sand-rubber mixtures was approximately linearly varied with the confining pressure at different rubber contents.
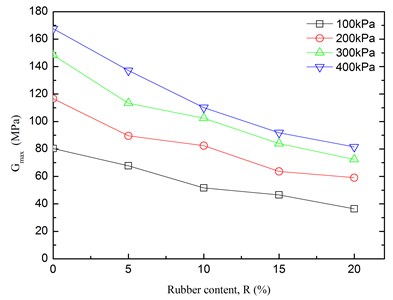
Fig. 11 depicts the relationships between the maximum dynamic shear modulus () of the sand-rubber mixtures and rubber content. It is found that the greater the rubber content was, the smaller the maximum dynamic shear modulus was. Moreover, the was approximately linearly decreased with the rubber content. And the elevated confining pressure caused the increase of the maximum dynamic shear modulus (), which is due to the low rigidity and high damping characteristics of the rubber material. As the rubber content increased, the sand content decreased in mixtures. The rubber particles increased the weak bonding at the interface between the rubber particles and the sand particles. The bonding between the sand particles was greatly reduced, and the strength of the mixtures was decreased. As a result, the overall stability of the mixtures was decreased, the stability of the mixture was destroyed by relatively small bonding force. Hence, the maximum dynamic shear modulus () of sand-rubber mixtures was reduced.
Fig. 10Relationships between Gmax and confining pressure
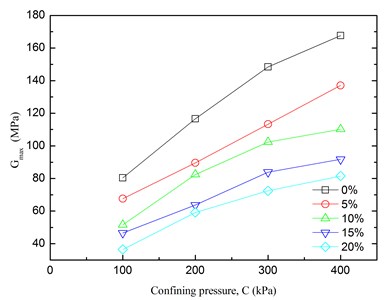
Fig. 11Relationships between Gmax and rubber content
3.4. Analytical expression of
There are usually two ways to determine the maximum dynamic shear modulus () of soils. The first method is to establish an empirical relationship based on laboratory tests, while the second way is to use in-situ shear wave velocity test results. According to the above analyses, it is found that the confining pressure and rubber content are the two main influence factors for . Fig. 12 presents three-dimensional relationship among confining pressure, rubber content and . As shown in Fig. 12, the matrix network that was composed of the three factors was approximated as an oblique surface in three-dimensional space. The relationship between the maximum dynamic shear modulus and confining pressure and rubber content is proposed:
where is the rubber content, %; is the confining pressure, kPa; is the atmospheric pressure, kPa; , , , are the fitting parameters. According to the regression analyses, the fitting parameters were obtained as 0.27, 0.41, 0.66, 0.53. The comparison of between predicted values by Eq. (1) and experimental results is shown in Fig. 13. It is found that the predicted values were in a very good agreement with the experimental results.
Fig. 12Relationship among confining pressure, rubber content and Gmax
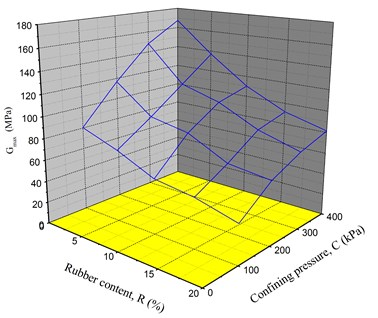
Fig. 13Comparison of Gmax between predicted values and experimental results
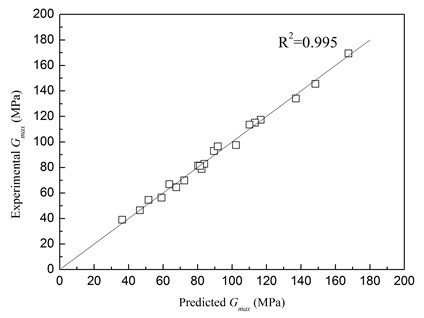
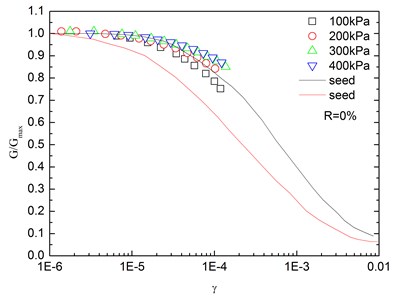
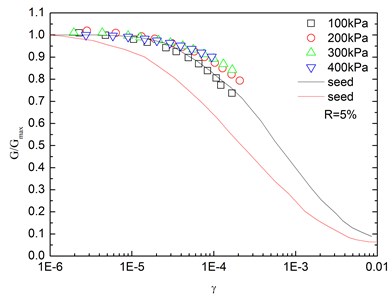
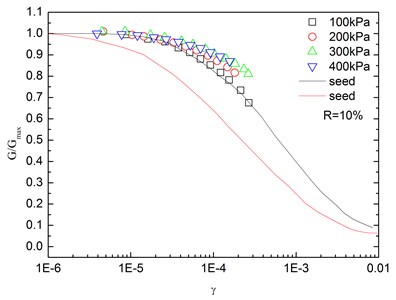
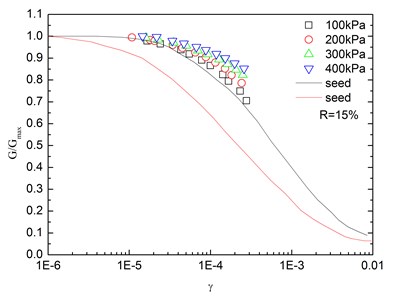
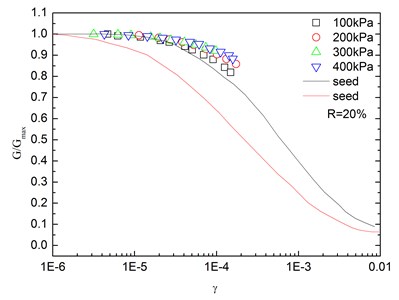
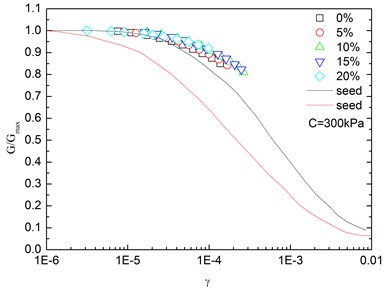
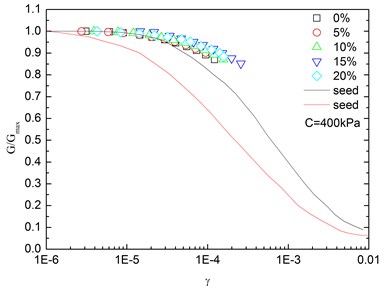
Fig. 14Relationships between G/Gmax and shear strain at varying confining pressures (Note: R refers to rubber content)
a)
b)
c)
d)
e)
3.5. - characteristics
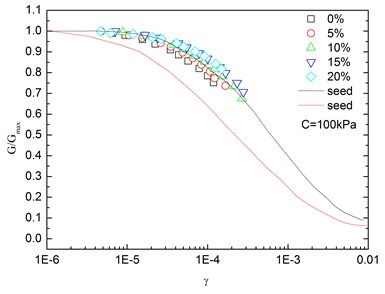
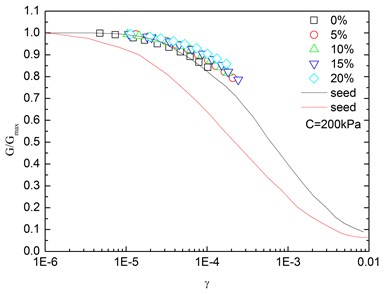
Fig. 14 presents the relationships between and shear strain () at varying confining pressures. It is indicated that the - curves at different confining pressures were concentrated in a very small band with little discretization, and the effect of confining pressure on - relationship was not prominent. Moreover, the increased confining pressure caused a slight increase in in the entire test range of shearing strain amplitude. The values of the sand-rubber mixtures were in the vicinity of the upper envelope of the - curves of sands proposed by Seed and Idriss [15]. It is also indicated that the test results were very close to the upper envelope of - curves suggested by Seed and Idriss [15]. Similarly, Fig. 15 presents the relationships between and shear strain at varying rubber contents. It is found that the rubber content had a small effect on .
Fig. 15Relationships between G/Gmax and shear strain at varying rubber contents (Note: C refers to confining pressure)
a)
b)
c)
d)
4. - characteristics
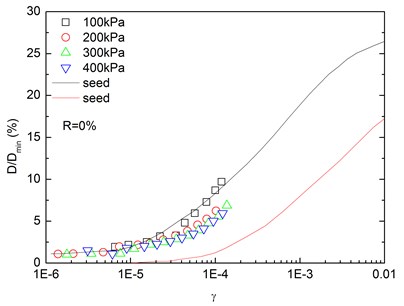
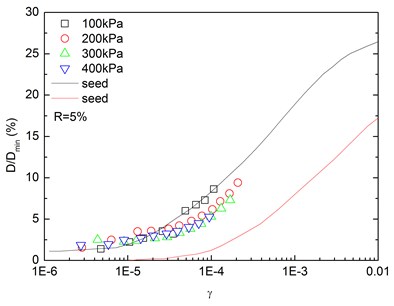
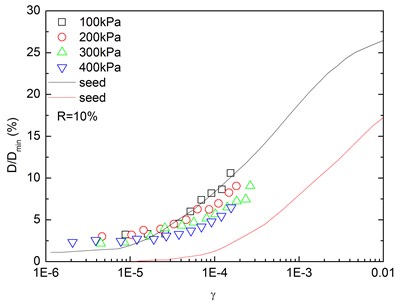
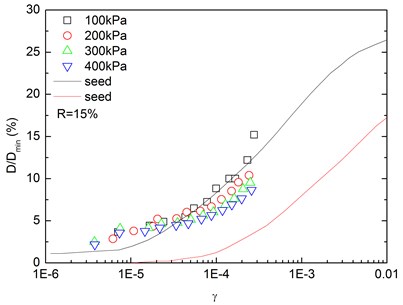
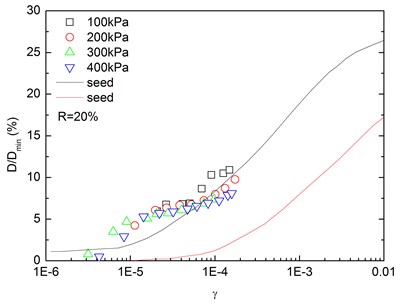
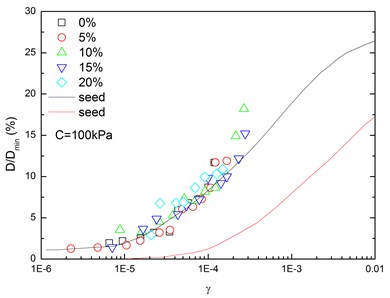
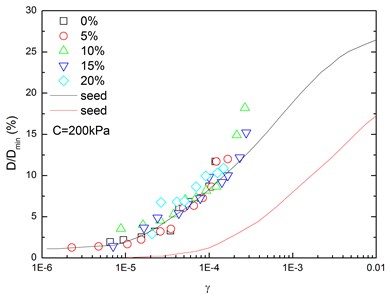
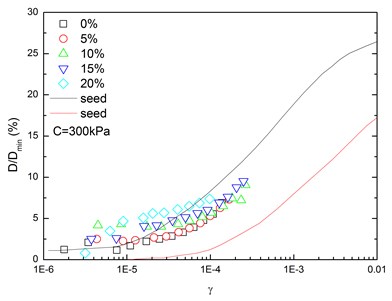
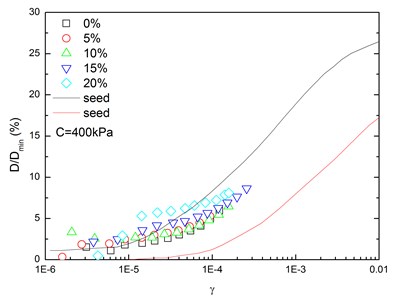
Fig. 16 presents the relationships between normalized damping ratio () and shear strain () at varying confining pressures. At the same confining pressure, the normalized damping ratio of sand-rubber mixtures was concentrated in a narrow strip-shaped region, and the discrepancy of the experimental value of normalized damping ratio between different confining pressures was small. It is also found that the normalized damping ratio of the mixtures was located near the upper envelope of - curve proposed by Seed and Idriss [15]. The higher the confining pressure was, the smaller the peak value of normalized damping ratio was. In addition, the effect of confining pressure on normalized damping ratio of the mixtures was not obvious. Similarly, Fig. 17 presents the relationships between normalized damping ratio () and shear strain () at varying rubber contents. It is indicated that the increased rubber content led to a slight increase of peak value of the normalized damping ratio. The experimental normalized damping ratio of the mixtures was located near the upper boundary suggested by Seed and Idriss [15].
Sand-rubber mixture has characteristics of light-weighted, high strength, and excellent anti-seismic ability, thereby it has a great potential to be used as construction materials in civil/geotechnical engineering [5, 11]. The resource utilization of waste rubber materials also reduces the increase in waste tire and beneficial to environmental protection. However, the engineering applications of sand-rubber mixtures is still rare because of the uncertainty of its dynamic and mechanical behavior, and the effect of rubber content on those properties. Long-term performance of this material regarding the settlement, and compaction issue that might be encountered in construction stage are still less understood. Hence, further study will be conducted on this topic, and it will be presented in a companion manuscript.
Fig. 16Relationships between normalized damping ratio and shear strain at varying confining pressures (Note: R refers to rubber content)
a)
b)
c)
d)
e)
Fig. 17Relationships between normalized damping ratio and shear strain at varying rubber contents (Note: C refers to confining pressure)
a)
b)
c)
d)
5. Conclusions
In this study, the dynamic properties of sand-rubber mixtures in a small range of shearing strain amplitude (10-6-10-4) were studied by a series of resonant column tests. The effects of shearing strain, rubber content and confining pressure on the dynamic properties (i.e. dynamic shear modulus, damping ratio, maximum dynamic shear modulus) of the mixtures were also investigated. The major conclusions resulting from this study can be drawn as follows. The increase of shear strain reduces the maximum dynamic shear modulus, but increases the damping ratio of the sand-rubber mixtures. As the dynamic shear modulus of the mixtures increases, the damping ratio decreases with an increase in confining pressure. As the dynamic shear modulus decreases, the damping ratio increases with an increase in rubber content. The confining pressure has a significant effect on the maximum dynamic shear modulus of the mixtures. Based on the experimental results, the empirical formulas of the maximum dynamic shear modulus considering the effects of confining pressure and rubber content are proposed. The normalized dynamic shear modulus are concentrated in the narrow strip area, and the discrepancy is small between different confining pressures. All the experimental values of are near the upper boundary of the - curves proposed by Seed and Idriss [15]. As the confining pressure increases, the - curve approaches upward, indicating that the degree of attenuation is reduced. The normalized dynamic shear modulus is increasing with the increase in rubber content. When the rubber content is small, it is closer to the upper boundary of the - curve, which shows that the dynamic behavior of mixtures is more like sand material.
References
-
Wen C., Xu H. S. Review of resource utilization of waste tires. Resources Economization and Environmental Protection, Vol. 22, Issue 3, 2006, p. 7-9, (in Chinese).
-
Senetakis K., Anastasiadis A., Pitilakis K. Dynamic properties of dry sand/rubber (SRM) and gravel/rubber (GRM) mixtures in a wide range of shearing strain amplitudes. Soil Dynamics and Earthquake Engineering, Vol. 33, Issue 1, 2012, p. 38-53.
-
Edil T. B., Bosscher P. J. Engineering properties of tire chips and soil mixtures. Geotechnical Testing Journal, Vol. 17, Issue 4, 1994, p. 453-464.
-
Foose G. J., Benson C. H., Bosscher P. J. Sand reinforced with shredded waste tires. Journal of Geotechnical Engineering, Vol. 122, Issue 9, 1996, p. 760-767.
-
Tsang H. H., Sheikh M. M., Lam N. Rubber-soil cushion for earthquake protection. Australian Earthquake Engineering Society Conference, 2007, p. 1-8.
-
Zornberg J. G., Viratjandr C., Cabral A. R. Behaviour of tire shred-sand mixtures. Canadian Geotechnical Journal, Vol. 41, Issue 2, 2004, p. 227-241.
-
Humphrey D. N., Manion W. Properties of tire chips for lightweight grouting soil, improvement and geosynthetics. ASCE, Geotechnical Special Publication, Vol. 30, 1992, p. 1344-1355.
-
Zheng Y. F., Sutter K. G. Dynamic properties of granulated rubber/sand mixtures. Geotechnical Testing Journal, Vol. 23, Issue 3, 2000, p. 338-344.
-
Anastasiadis A., Senetakis K., Pitilakis K. Dynamic behavior of sand/rubber mixtures. Part I: Effect of rubber content and duration of confinement on small-strain shear modulus and damping ratio. Testing and Specification of Recycled Materials for Sustainable Geotechnical Construction, ASTM International, Vol. 9, Issue 2, 2012, p. 1-19.
-
Nakhaei A., Marandi S. M., Kermani S. S., Bagheripour M. H. Dynamic properties of granular soils mixed with granulated rubber. Soil Dynamics and Earthquake Engineering, Vol. 43, 2012, p. 124-132.
-
Nakhaee A., Marandi S. M. Reducing the forces caused by earthquake on retaining walls using granulated rubber-soil mixture. International Journal of Engineering-Transactions B: Applications, Vol. 24, Issue 4, 2011, p. 337-350.
-
Zhong X. G., Zeng X., Rose G. Shear modulus and damping ratio of rubber-modified asphalt mixes and unsaturated subgrade soils. Journal of Civil Engineering, Vol. 14, Issue 6, 2002, p. 496-502.
-
Christ M., Park J. B., Hong S. S. Laboratory observation of the response of a buried pipeline to freezing rubber-sand backfill. Journal of Materials in Civil Engineering, Vol. 22, Issue 9, 2010, p. 943-950.
-
ASTM D2487-11. Standard Practice for Classification of Soils for Engineering Purposes, Unified Soil Classification System, ASTM International, West Conshohocken, PA, 2011.
-
Seed H. B., Idriss I. M. Soil Moduli and Damping Factors for Dynamic Response Analyses. EERC, No. 0-10, 1970.
Cited by
About this article
This research was financially supported by the Natural Science Foundation of Jiangsu Province (Grant No. BK20161311) and Six Major Talent Peak in Jiangsu Province in China (Grant No. 2015-JZ-011).
Zhaoyu Wang is the leader of this paper. Nan Zhang is responsible for English writing and editing. Yong Jin, Qi Li, Xiaohui Chen are the students who conducted lab tests and summarize the test results.
