Abstract
The evolution of mechanical parameters, a factor affecting the mechanical reliability, has gathered more attention nowadays. However, studies on time varying uncertainty can hardly be found. A new method based on evolution-based uncertainty design (EBUD) is applied to the design of gear in this paper. Considering the wear evolution over the lifetime, a tooth wear’s time-varying uncertainty model based on the continuous-time model and Ito lemma is established. Drift and volatility functions dependent on the drift rate and volatility rate of rotational speed and torque are used to express the time-varying uncertainty of tooth thickness. The method can predict the reliability and provide an instruction in reliability improving, maintenance and repair of the gear system.
1. Introduction
Gear transmission is the most important and widely used transmission form in mechanical systems. Almost all of the mechanical systems, from mechanical watch to nuclear power station, contain the gear transmission systems. The gear transmission system is mainly responsible for the transferring torque and power of the mechanical system. Once a failure occurs, it will lead to the collapse of the entire mechanical system. And there are various forms of gear failure. Process, materials and other factors may reduce reliability of gear. Therefore, it is particularly important to ensure the reliability of gear.
At present, there are a lot of literatures on the reliability analysis of gear. Ryazantsev A. A. [1] presented A method to prolong the life and improve the reliability by using the surface quenching of the open gear on the spherical ore-pulverizing mills. Starzhinsky, Victor E. [2] considered the employment of different statistical distribution parameters for gear reliability prediction, and described a method of predicting gearing reliability as a relation of the acting and permissible stress distributions. Netpu, Samroeng [3] analyzed the failure mechanism of gear from the aspect of material impurity, and improved the reliability of the gear from the aspect of material processing. Most of the existing literature focuses on reliability analysis, but there is little research on the method of reliability design of gears. Alemayehu, Fisseha M. [4] presented a novel probabilistic multibody dynamic analysis (PMBDA) that enhances the deterministic design practice of gears and gear systems, and implemented an advanced mean based on fast probability integration method to perform a reliability analysis. However, most of existing literatures focus on reliability analysis. there is little research on the method of reliability design of gears, and the influence of time factor on the reliability of gear is seldom considered. So far, the essence of gear design method is safety factor method. In order to ensure safety, the value of safety factor is always higher than the requirement. So, it can get an optimum gear. As the service time increasing, fatigue, wear, aging and other factors result in mechanical parameters changes, which should be paid more attention in mechanical design. It is necessary to use Evolution-based uncertainty design (EBUD), which is proposed in reference [5-7], in the key gear of mechanical system to predict and extend the life, predict and improve reliability of mechanical systems.
In this paper, the compare between the practical and the allowable value of tooth thickness is used as the failure criterion. Considering time effects on the system uncertainties, the integrated wear model is employed in the calculation of spur gear reliability, using the gear wear as the time varying uncertain parameter. As we can see from the work below the new method literally improves the reliability and the life of the gear. The method can also be used in the design of bevel gear, helical gear, and face gear.
2. Mathematical model of EBUD
For general system, the system performance index or variables used in the describing system status can be modeled as a stochastic process. The system uncertainty (or probability under some conditions, or reliability) at any time can be solved by the probability model which is the inequality relation about the value of real system performance and the value of the system required to achieve.
In order to model the general probability expression of evolution-based uncertain individual design method of the system, based on the references [5], the system status is expressed by the system individual performance output and individual allowable performance output function [6-9].
System evolution-based uncertain with individual data: the risky (or safety) existing in the system, in which the system performance should satisfy the regulated requirement (expressed by the inequality relationship of performance output and allowable performance output) under the specified environmental conditions at the regulated time. It can be described by the uncertainty (unreliability), or can be calculated by the certainty (or reliability). Considering the time-dependent uncertain characteristic of the system, the EBUD mentioned in this paper is to give the feasible design solution under the acceptable risk or reliability of the system.
The quantitative expression of system evolution-based uncertain is reliability, which means the probability of the system meeting the allowable performance output under the stated environmental conditional at the regulated moment. The math expression of the system meeting the performance output is the inequality relationship between the performance output and allowable performance output . It is general expression can be described as Eq. (1):
If the system required that the performance output greater than or equal to the allowable performance output, those two output all multiply by –1:
The normalized form is:
According to the above definition, the system reliability over a time interval for the evolution-based uncertainty analysis can be written as Eq. (4) or (5):
According to the theory of EBUD, assumed the parameters (or ) obeys Geometric Brownian Motion. is drift rate of and volatility rate:
Then, according to the Ito Lemma [10]:
Which means that the random variable conforms logarithmic normal distribution.
On the basis of the extension of the Ito Lemma which aims at multiple random process, or (use to express) obeys Ito process:
The mean and variance are:
If the system requires , the system reliability must be:
If the requirement of system reliability is given, the original value of design variable must satisfy the Eq. (11):
3. Tooth wear evolutionary model
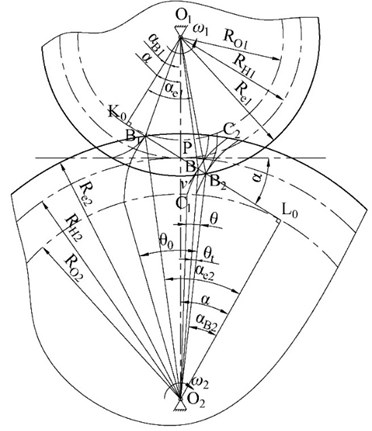
As is shown in Fig. 1, gear 1 and gear 2 are engaged. gear 1 is driving gear, and gear 2 is driven gear. B1 is the point which the tooth enters the meshing process, and B2 is the point which the tooth exit. In a pair of teeth meshing process, meshing time:
3.1. Calculation of wear rate parameters
Using the integrated wear model, the wear rate is considered to be related to the contact stress p and the relative sliding speed . The wear rate:
is wear coefficient, which is related to material and lubrication condition.
Relative sliding velocity of meshing point:
where , is meshing point’s radius of curvature. When the tooth profile is ideal involute, , :
Fig. 1Gear meshing contact stress at meshing point
Normal force of gear contact point :
Meshing point contact stress (calculated in accordance with Hertz formula):
3.2. Calculation of time varying wear thickness calculation:
Wear thickness in a pair of teeth meshing process:
Tooth contact is considered as tow cylinder contact approximately. Width of contact deformation:
Contact time:
mesh thickness ’s Natural logarithm:
In the actual situation, comparing with other parameters, the rotational speed and torque of the input vary largely with time’s changing. So, they can be considered as time-varying parameters. According to Eq. (7):
According to the Eq. (10):
conform to logarithmic normal distribution, whose expectation is:
And variance is:
The Edgeworth series method is used to approximate the normal distribution of the logarithm normal distribution when calculating the total wear [11]. That is:
– standard normal distribution function:
– Standard normal distribution probability density function:
is order Hermite orthogonal polynomials:
: standard deviation of log normal distribution.
: third-order moments of lognormal distribution.
: fourth-order moments of lognormal distribution.
After the substitution, the original equation can be regarded as the normal distribution. The expectation of total wear thickness is , the variance is . Time varying tooth backlash obeys normal distribution whose expectation is , and variance is approximately.
4. EBUD of gear
The conditions of gear transmission are as follows. Transmission ratio is required ranging from 2.5-3, center distance ranging from 150-200 mm. The rotational speed 400 r/min when smooth running. The torque 110 N·m, this gear system works 8 h every day, 260 days a year. The failure criterion is that the tooth thickness of root circle is less than 90 % of initial tooth thickness. the material is steel and the lubrication condition is well, that is 3×10-4. The wear reliability is required not less than 97.5 % after 8 years. Assumed that drift rate and volatility rate of rotational speed and torque is 2×10-11, 1×10-10.
Table 1The parameters of standard gear pairs
Small gear | Big gear | |
Modulus ( / mm) | 3 | 3 |
Number of teeth () | 35 | 95 |
Pressure angle ( / °) | 20 | 20 |
Center distance ( / mm) | 195 | |
Pitch diameter ( / mm) | 105 | 285 |
Addendum circle diameter ( / mm) | 111 | 291 |
Root circle diameter ( / mm) | 97.5 | 277.5 |
Base circle diameter ( / mm) | 98.67 | 267.81 |
Tooth width ( / mm) | 110 | 105 |
Tooth thickness of pitch circle ( / mm) | 4.71 | 4.71 |
Tooth thickness of root circle ( / mm) | 5.91 | 7.07 |
Rotational speed when running smoothly (/ (r/min)) | 400 | 147.6 |
Elastic modulus (/ MPa) | 200 | 200 |
Poisson ratio | 0.3 | 0.3 |
Transmission ratio | 2.71 | |
The parameters of gear are determined after analyzing the gear’s failure mode and determining design criterions as is shown in Table 1.
According to the rotational speed and torque, a pair of teeth in the meshing frequency of the whole life cycle is 8×260×8×60×400 = 3.2×109.
(1) Determining the meshing time in a pair of teeth meshing process.
According to Fig. 1 and Table 1, 0.425, 0.308, so [0,7.6×10-3]
(2) Calculation of wear rate parameters.
According to Table 1 and Eqs. (13), (14), (16), (17), the wear thickness of small gear is shown in Fig. 2.
Fig. 2The function image of wear rate and time of one pair of teeth meshing
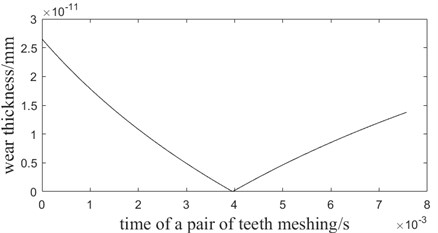
As is shown in Fig. 2, when 0, the wear thickness of root is 2.6513×10-11 mm.
(3) Calculation of time varying wear thickness calculation.
According to Eq. (21), (22), (23), and the time varying parameters of rotational speed and torque, conform to logarithmic normal distribution, whose expectation is 0.0890, and variance is 0.0728. The allowable wear thickness 5.91×10 %0.591 mm, so the reliability:
The reliability cannot meet the requirements.
In order to satisfy the requirement of wear, positive correction should be used on designing the small gear. Modification coefficient 0.2. So, the modification coefficient of big gear is –0.2. The root circle diameter of small gear 97.5+2×0.2×3 98.7 mm, tooth thickness of root circle change to 6.35 mm. After modification, the wear thickness of small gear is shown in Fig. 3. When , the wear thickness of root is 1.9290×10-11 mm
Fig. 3The function image of wear rate and time of one pair of teeth meshing after modification
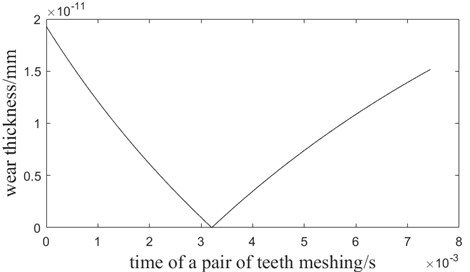
The allowable wear thickness6.35×10 % = 0.635 mm. conforms to logarithmic normal distribution, whose expectation is 0.0648, and variance is 0.0728. The allowable wear thickness5.91×10 % = 0.591 mm, so the reliability:
The reliability can meet the requirements. Compared with original scheme, the tooth thickness changes from 5.91 mm to 6.35 mm, and the reliability improves from 97.06 % to 98.21 %.
5. Conclusions
The method of EBUD for gear systems is proposed in this paper considering the evolution and uncertain characteristics existing in the system. The drift function and the volatility function of the tooth thickness, the time varying parameters, are determined by the drift rate and the volatility rate of the rotational speed and torque. So, the tooth thickness is regarded as performance output, the allowable tooth thickness being the allowable performance output. They can reflect the uncertainty and evolution characteristics of the system. The gear system reliability model expressed in EBUD, inequality relationship of performance output and allowable performance output, is established on the basis of Ito Lemma and Ito Process. It can be calculated at any time by using the data of the system variables. By using EBUD, the reliability of gear increased by 1.15 %. This paper presents a new method for reliability design of gears, which has practical engineering significance.
References
-
Ryazantsev A. A. Analysis of means of reliability and service life growth for open gear drive of ore-pulverizing mills. Metallurgical and Mining Industry, Vol. 6, Issue 4, 2014, p. 6-22.
-
Starzhinsky Victor E., Soliterman Yuri L., Goman Arcadi M. Reliability prediction of gear transmissions. Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, New York, 2008, p. 165-172.
-
Netpu S., Srichandr P. Failure of a helical gear in a power plant. Engineering Failure Analysis, Vol. 32, Issue 9, 2013, p. 81-90.
-
Alemayehu F. M., Ekwaro-Osire S. Uncertainty considerations in the dynamic loading and failure of spur gear pairs. Journal of Mechanical Design, Transactions of the ASME, Vol. 135, Issue 8, 2013, p. 084501.
-
Shi B. Q., Duan G. C., Shen Y. H., et al. Evolution-based uncertainty design for complex mechanical systems. Journal of Xi’an Jiaotong University, Vol. 49, Issue 3, 2015, p. 80-86.
-
Shi B. Q., Yan Y. Y., Fan H. F., et al. Mechanical design method with uncertain evolution. Journal of University of Science and Technology Beijing, Vol. 30, Issue 9, 2008, p. 1050-1054.
-
Yan Y. Y., Shi B. Q. Time dependent reliability analysis under uncertainty. Journal of Xi’an Jiao Tong University, Vol. 41, Issue 11, 2007, p. 1303-1306.
-
Li S. Lubrication and contact fatigue models for roller and gear contacts. The Ohio State University, 2009.
-
Miryam B. S., Miguel P., Jose I. P. Calculation of tooth bending strength and surface durability of internal spur gear drives. Mechanism and Machine Theory, Vol. 95, 2016, p. 102-113.
-
Ruey S. Tsay Analysis of Financial Time Series. Posts and Telecom Press, Beijing, 2010.
-
Cramer H. Mathematical Methods of Statistics. Princeton University Press, New Jersey, 1964.
