Abstract
A fully automatic washing machine with vertical pulsator and 10 kg load capacity has most violent shake and or vibration, and worst dynamic stability, which result in maximum noise in dehydration. The mechanisms of noise generation and motions at stage of dehydration are analyzed. Dynamic impacting excitation is firstly clarified as the most important dominant factor in understanding acoustic behavior of the washing machine at the stage. A new damper is developed and designed on the basis of improving the degree of harmonics (DOH) of dynamic impacting force, which is employed as the critical criterion for damper design. Applying the damper developed reduces the washing machine noise 2.2 dB(A) and 4.7 dB(A) under conditions of normal and worst unbalance respectively.
1. Introduction
In home-appliance industry, marketing competition forces product performances coming up higher and higher level of dynamic product quality, including stricter specifications, limitation on noise and vibration level, and dynamic stability [1]. For washing machines, conventional investigations concentrated on vibro-behaviors [2], there came out different sorts of developments, such as analysis on dynamic characteristics [3, 4], damping vibro-reduction [5, 6], and structural designs [7-10], etc. Some effects of noise and vibration reduction were achieved to different extent. A washing machine generates maximum noise, resulted from heavy vibration and dynamic instability during dehydration [11], especially for large volume products with vertical pulsator. Solving such dynamic quality problem in dehydration is an important issue. Where, design dynamic performance of the key part “damper” in the suspension system of “out-case and tub” plays critical role. There were a number of patents [12-17] and researches [18-20] on it. However, they focused on improving the transient stability of the tube and whole machine in dehydration. In fact, the dampers directly affect the vibration and noise of whole product in steady state. Improper damper design may increase product noise and vibration. Therefore, developing new damper system to keep either better transient stability or low noise and vibration is a significant topic.
Most of existing investigations on dynamic behaviors of a fully automatic washing machine are focused on vibration reduction and thus reducing noise. The conventional techniques include damping, vibration insulation, sound absorption and dynamic design of structures. They make the noise and vibration reduction of most current washing machines to different extent. For the washing machine with vertical pulsator and 10kg load capacity, which is investigated in this paper, its noise level is currently in the range of 50-55 dB(A), depending on cloth load condition and speed pattern.
In this paper, the interactions between out-tub assembly and out-case of the washing machine in dehydration is explained with description on mechanism of vibration and noise generation. It is firstly put forward that the interaction is a periodical impacting process in essence and washing machine noise depends on the impacting force, especially its spectrum. In view of that, a new damper with two-stage of damping function is developed to reduce the washing machine noise. Its application makes the washing machine noise reduced 2.2 dB(A) and 4.7 dB(A) respectively for normal and worst unbalance condition, with keeping the original vibratory response in dehydration. Some simulating and experimental results were also shown with relevant explanations.
2. Noise generation and motions of the washing machine
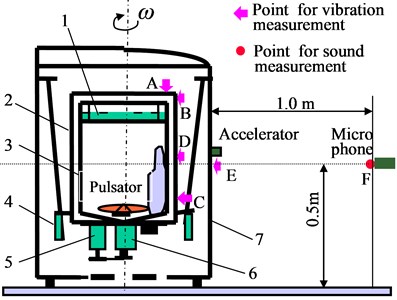
A vertical fully automatic washing machine consists mainly of 3 components: out-tub (O/T) assembly, suspension system, i.e., dampers, and out-case (O/C). Where, O/T-assembly is the major body of motions in the washing machine, which consists of motor as power source, clutch, inner-tub (I/T) with auto-balancer and O/T-shell. Fig. 1 shows its scheme.
Fig. 1Scheme of fully automatic washing machine and measurement points: 1 – auto balancer, 2 – out-tub (O/T), 3 – inner-tub (I/T), 4 – damper, 5 – motor, 6 – clutch, 7 – out-case (O/C)
3. Noise Generation
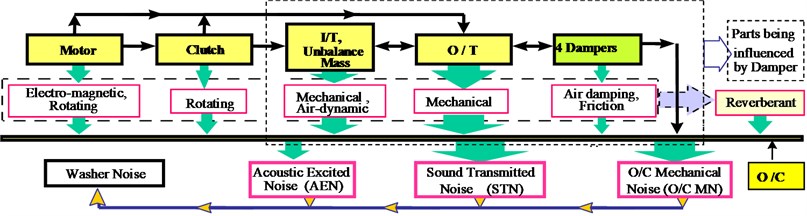
Usually, strong vibration and noise in process of dehydration represent dynamic performances of the washing machine. Fig. 2 shows the interactions between different components in the operating process. The I/T is driven by motor-clutch to rotate at speed with fixed pattern. Under the force action of unbalance mass formed by clothes, O/T-assembly will be excited by the I/T with unbalance mass periodically, and thus it acts on O/C by dampers. Each components generates their own noise: electro-magnetic noise from motor, rotating noise from motor and clutch, air-dynamic noise from I/T and damper, mechanical or structural-bone noise from I/T, O/T shells and O/C. There is also reverberant effect in O/C and acoustic excitation on O/C. The washing machine noise thus consists of 3 parts: O/C mechanical noise, sound transmitted noise and acoustic excited noise, see Fig. 2.
Fig. 2Noise generation of fully automatic washing machine
In all the noise radiations, if motor-clutch is designed perfectly, noise from them will be low enough to be omitted, especially when the strong mechanical noises in Fig. 2 are excited by very large unbalance mass in rotation with I/T. Fig. 3 shows the noise spectrums at point F in Fig. 1, under excitation of equivalent unbalance mass 0.75 kg, say it ‘worst unbalance condition’, in steady stage of dehydration with rotating speed 750 rpm. It shows that, washing machine noise has good coherence with vibration of O/T and O/T shell, and it is mainly contributed by mechanical sound radiation (including acoustic excitation effect) of O/C at low frequency, and by that of O/T-assembly at mid-high frequency.
If the and are constants, the washing machine noise will depend mostly on the performance of dampers which influence noise generations of all parts in the block with dot-line in Fig. 3. Therefore, four dampers in the washing machine are very important key parts to dynamic behaviors, both vibration and noise.
Fig. 3a) Noise spectrum at F in worst case, b) vibrational response at E on O/C, c) coherence between noise at F and vibration at D(O/T) and E(O/C)
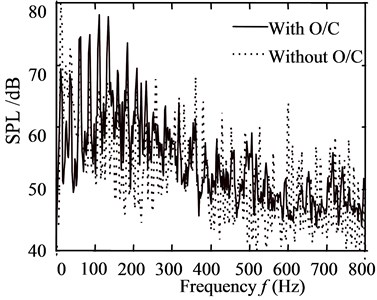
a)
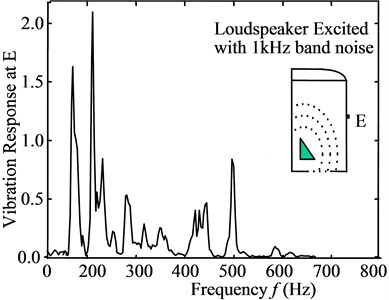
b)

c)
4. Modes of O/T-assembly motion
As mentioned above, O/T-assembly moves under excitation of unbalance mass rotating periodically. If it is considered as a rigid body, and O/T shell and motor-clutch are jointed rigidly with I/T and auto-balancer, the motions of O/T-assembly can be determined by the following equations:
where:
and , , are respectively driving torque of clutch for I/T, unbalance mass and eccentricity radius, , , are rotating inertia in -, -, -axis (). Symbols , , , , , , and are shown in Fig. 4, and is equivalent damping coefficient of damper. Gyro effect is also taken into account. Three modes of motion with Eq. (1) can also be seen in Fig. 4. They are flat motion, rotation and twist. The motion of O/T-assembly can be considered as linear composition of the 3 coupled modes. The horizontal vibration at point N and vertical vibration at top of O/T in Fig. 4(a) can be obtained as:
Fig. 4Three modes of O/T assembly motion
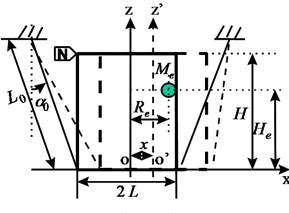
a) Flat motion
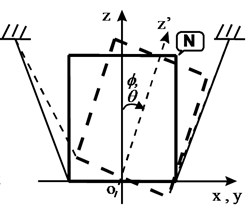
b) Rotation
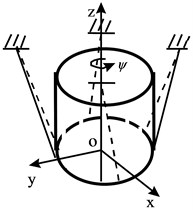
c) Twist
It can be proved that and have also periodical characteristics. Their numerical solutions are shown in Fig. 5. It seems that the 1st mode and 2nd mode have the most important contribution to the transient response of O/T-assembly. With the rotating speed increases, the motion tide eventually into steady stage in which washing machine noise depends on the sum of vertical and horizontal vibration of the assembly.
5. Impacting process and force
5.1. Impacting excitation
In the modes described in Section 2, the flat motion (1st mode) of gravity center of the assembly and rotation (2nd mode) around - or -axis play an important part respectively in horizontal and vertical vibration respectively in transient response. Under the periodical excitation by rotating unbalance mass, vibration of O/T-assembly in steady stage of dehydration is mainly composed of them. While, the 3rd mode, twist, can be omitted in this situation. Such a composed vibration can be understood as an impact process, that is, in each cycle of rotation, the 1st and 2nd mode of motion make O/T-assembly impacting O/C once by path of the four dampers. That forms the periodical impact process between the assembly and O/C. In general, impact action between mechanical structures generates two types of mechanical noise: accelerate noise and velocity noise which is so called self-ring noise. The former comes from medium, air excited by dramatic speed variation of impacted bodies, say, O/T-assembly and O/C. It depends mostly on impact time and structural dimensions, volume . Its maximum sound pressure level can be described by [22, 23]:
where , and are respectively initial impacting speed, distance of calculated point to impacted bodies and sound speed in air, and is a constant. If normalized impact time , the impact process is of soft impact for which the accelerate noise will be too small to be omitted. For the washing machine described in this paper, 1/12.5 Hz 0.08 s, 0.184 m3, thus 47.842. Therefore, the accelerate noise of washing machine in steady dehydration can be considered as very small. The velocity noise can be also estimated by the following formula in principle:
where, , , , and are respectively impacting force spectrum, imaginary part of impacting vibratory response, efficiency of sound radiation, damping loss factor and thickness of impacting structures. is also a constant. Obviously, if the structures of O/T-assembly and O/C have been designed with a certain size, materials, shapes, etc., , , and will be determined. And the velocity noise will depend only on the impacting force , which is to be explained in next section.
5.2. Impacting force
In the periodical impact process acting on both O/T-assembly and O/C, impacting force is the dynamic force in dampers. It consists of two components, spring force and damping force . That is:
where, is stiffness of the spring. To reduce the velocity noise, the effective 2 ways are: (1) Reducing the magnitude of impacting force , which can be realized by reducing unbalance mass, such as the existing auto-balancer; (2) Modifying the spectrum to make its most energy existing in such frequency ranges that of the impacted structures is relative low. It requires perfect design of impacting force for practical product.
As mentioned in section 3.1, in transient stage of dehydration, the O/T-assembly has usually very large displacement response, which makes probably the assembly striking O/C sometimes. Thus the dampers in suspension must have enough damping instant force to prevent from the striking. Therefore, dampers in most of existing washing machines use dry friction force as the damping force, see Fig. 6(a). Because of tapered angle of damper cab, the friction force is somewhat vary with time. The forces can be described as:
Fig. 6a) Old damper and b) new damper
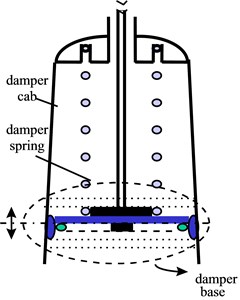
a)
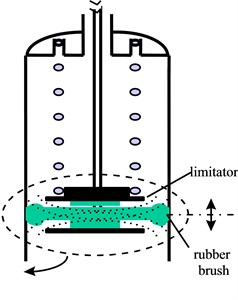
b)
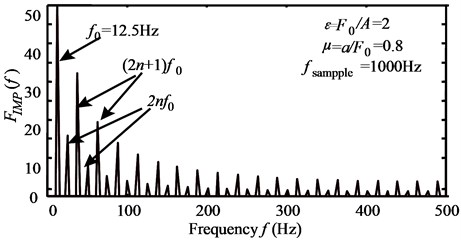
Fig. 7a) Impacting force (T=1/f0= 0.08 s, μ=a/F0= 0.08) and b) spectrum of impacting force
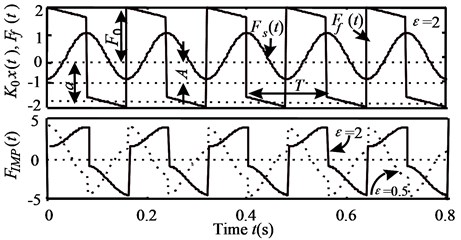
a)
b)
The parameters in Eq. (6) can be seen in Fig. 7(a). Fig. 7 shows such a impacting force in time and frequency domain. It can be seen that, the spectrums with peak values are of harmonics of fundamental . More-over, the magnitudes at are much larger than that of . Under excitation of this impacting force, there will be two types of vibratory response of O/T-shell and O/C: one is rigid modes vibration with the same spectrum of the force, the other is flexible modes which depend on structural flexible modal response and sound radiation coefficient, . They compose together into the resultant washing machine noise. Fig. 8 gives a group of such results tested on the real washing machine. And the tested impacting force can be also seen in Fig. 9(a). Fig. 8(a) shows that there are rich acoustic responses to the impact excitation on O/T-shell and O/C by testing hammer. And the tested vibratory responses of the washing machine in operating agree with this analysis well.
Fig. 8a) Force-acoustic response of O/T & O/C, and b) vibration of O/T & O/C in dehydration, (Vr= 750 rpm)
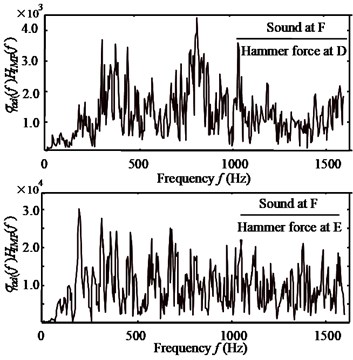
a)
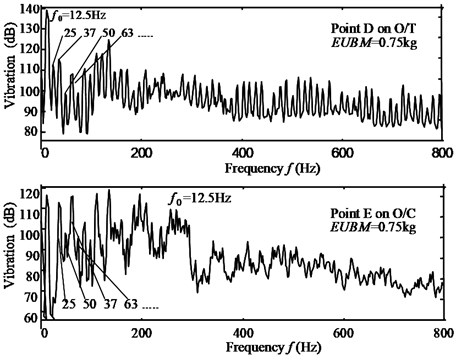
b)
6. Damper redesign and its performances
In order to improve the impact force spectra of the old damper shown in Fig. 6(a), current damping force has to be modified mainly to suppress harmonics in the spectra. Here, degree of harmonics () is defined as a new parameter for assessment on impacting force of the damper:
That is the energy ratio between harmonics and fundamental of force spectrum. The lower is, the less harmonics in impacting force. The existent probability of excited vibratory responses and or its magnitudes will be afterwards smaller, both for rigid modes and flexible modes. If 0, there is only fundamental – the ideal situation. For the old damper, Fig. 6(a), its impact force, Fig. 8(a), has high value, 175 %. But the large vibratory response in transient stage needs to be suppressed by enough instant damping force, as mentioned before, such as friction force. A new damper with 2-stage functions, as shown in Fig. 8(b), has been designed and developed. In principle, there is friction force when the vibratory response is large enough in transient stage. The friction damping reduces as the steady stage coming and the response being small. In this stage, there comes the structural damping due to the bending brush. The impact force excites the harmonic vibration at low .
Fig. 9 compares the transmitted forces, tested by load cells under worst condition 0.75 kg, and noise spectra when the old and new dampers is used. It shows that the new damper is effective for washing machine noise reduction, 4.7 dB(A) lowered. of the new damper is 34 %, much lower than old damper. In addition, the other results are (1) Noise reduction by the new damper as is 0.3 kg, 0.4 kg at upper and lower positions is 2.2 dB(A); (2) The new damper has no influence on the transient vibration, 21 mm, 12 mm; (3) The damping coefficient of the new damper at the simulating steady stage is 62.3 Ns/m, doubled the old damper (27.7 Ns/m). Therefore, the new damper dynamic performances are satisfied for noise reduction and practical requirements.
Fig. 9a) Transmitted force, and b) noise reduction by new damper
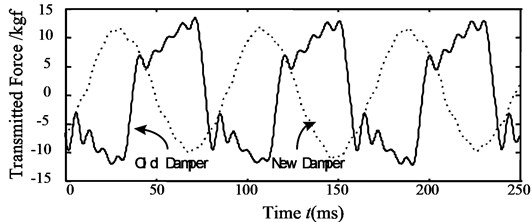
a)
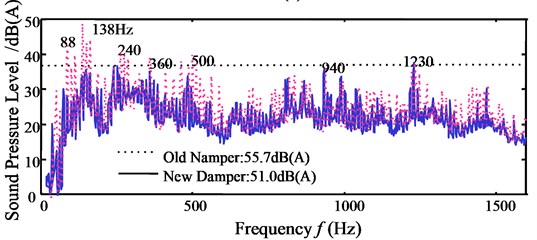
b)
7. Conclusion
In a fully automatic washing machine with vertical pulsator, the interaction in dehydration between out-tub assembly and out-case can be understood as a periodical impact process via the suspension dampers, under the excitation of rotating unbalance mass. The dampers affect the washing machine vibratory and acoustic responses. Improving the spectra of impact forces in dampers is a feasible and effective scheme to suppress impact excitation on the components generating noise, thus the washing machine noise can be reduced correspondingly. The new damper developed has good performances to improve the dynamic behaviors of the washing machine, especially on noise reduction, 2.2 dB(A) and 4.7 dB(A) lower under normal and worst unbalance conditions respectively in dehydration.
References
-
Liu S. Current state and strategies of home-appliances. Commercial Products and Quality, Issue 2, 2012, p. 307-307.
-
Song J. N. Specifications for “vibro-performances of washing machines” – guides for vibration reduction. Home Appliances, Issue 1, 2012, p. 37-37.
-
Wang Z. W., Wu H. H. Analysis and simulation on dynamic characteristics of top-loading washing machine. China Mechanical Engineering, Vol. 13, Issue 23, 2002, p. 2033-2035.
-
Chen S. T., Yue J. S., Xu Z. G. Detailed explanation on testing data of noise and vibration for washing machines. Technology of Home Appliances, Issue 7, 2015, p. 34-36.
-
Zheng H. M., Liu Z. S., Li Z. Y. Experimental study on vibro-analysis and vibration reduction of new type of slant axial washing machine. Experimental Mechanics, Vol. 19, Issue 4, 2004, p. 477-482.
-
Xu C., Zhuo Y. Y., Li X. C. Vibration and noise control of drum washing machine. Environmental Engineering, Vol. 26, Issue 1, 2008, p. 57-60.
-
Zheng H. M., Liu L., Jia W. Y. Application of WBS to noise reduction of washing machine. Light Industrial Machines, Vol. 25, Issue 1, 2007, p. 122-124.
-
Gu Q. K., Zhang S. P., Li C. Y., et al. Development on washing machine with low vibration and noise. Noise and Vibration Control, Issue 5, 2003, p. 42-44.
-
Liu B., Feng T., Wu X., et al. Analysis on working deformations and noise at low frequencies of slant drum washing machine. Noise and Vibration Control, Issue 3, 2010, p. 50-54.
-
Gu C. L., Zhou F. C., Xiang H. Y. Analysis on vibrational and noise issues of drum washing machines. Proceedings of National Conference on Home-appliances, Ningbo, Zhejiang, China, 2014, p. 386-391.
-
Xu Z. G., Lu J. G., Zhao W. B., et al. Investigation on Criterions in grades of vibro-performance tests for washing machines. Electric Equipments, Supplement, S1, 2011, p. 238-241.
-
Assembling Structure of Dampers for Washing Machine. LG Electronics, Inc., Patent No. 200410031382.0, 2004.
-
Dampers of Washing Machine. LG Electronics, Inc., Patent No. 200410043167.2, 2004.
-
Dampers and its Control Method of Washing Machine. LG Electronics, Inc., Patent No. 200510006555.8, 2005.
-
Damper Components of Drum Washing Machines. Lejin Electronics (Tianjing) Co., Patent No. 200410018886.9, 2004.
-
Damper Used for Washing Machine. Hitachi Production Co. Ltd., Patent No. 200510076213.3, 2005.
-
Hydraulic Damper of Drum Washing Machine. Lejin Electronics (Tianjing) Co., Patent No. 200510013753.7, 2005.
-
Masiro K. T. Noise reduction of fully automatic washing machine. Home Appliances, Vol. 65, Issue 4, 1991, p. 39-42.
-
Tatsmi H., Ito M. Vibration control methods of automatic washing machines. Noise Control, Vol. 9, Issue 1, 1985, p. 29-33.
-
Wu H. X., Dong G. Z., Qin L. G., et al. Modification of spider gear back to uniform the stress and improve the anti-wear performance of a real thrust washing machine. Engineering Failure Analysis, Vol. 60, 2016, p. 107-116.
-
Nashif A. D., Jones D. G. Vibration Damping. A Wiley-Inter-Science Publication, 1985.
-
Sun J. C. Principle of Mechanical Noise Control. Northwestern Polytechnology University Press, 1993.
About this article
The authors acknowledge gratefully the National Natural Science Foundation of China for supporting the researches of Project No. 51475211, including the study of this paper.
