Abstract
Mechanical assembly is important process affecting product dynamic quality. To completely inspect assembly quality, dynamic characteristic analysis is necessary. Based on substructuring dynamic analysis, this paper theoretically analyzes the changes of dynamic characteristics due to assembling process. Assembly coupling dynamic stiffness computed by inverse substructuring analysis is considered as a critical measure on the changes. The results obtained have been well validated by a lumped-parameter model for two-level of substructures.
1. Introduction
A mechanical assembly process is an important process in manufacturing electromechanical products. Its quality inspection and control are currently concentrated in “static quality”, such as shaping and positioning tolerances, size coordinations, etc., according to relevant technical standards and specifications [1]. The static quality is however incomplete for its dynamic property. It results in poor theoretical and thus technical guidance for dynamic quality inspection and control. To improve product dynamic quality further, Analysis on dynamic property of mechanical assembly further in detail is necessary in technology.
A mechanical assembly can be modeled as two-level of substructures. It is convenient to analyze the assembly dynamic property by use of substructuring dynamic analysis [2] and newly-developed inverse substructuring dynamic analysis. Where, Frequency Response Function (FRF) is often employed for structural dynamic analysis [3]. The spectral-based FRF inverse substructuring dynamic analysis has been well developed [4] theoretically and applied in automotive [5]. The first author of this paper [6] also applied the inverse substructuring analysis to analyze dynamic properties of a transportation packaging system.
This paper applies substructuring dynamic analysis to explain dynamic characteristics of a mechanical assembly process, based on relationship of FRFs of substructures and assembly system. Then, affects of the process on dynamic characteristics of either assembling substructures or assembly unit system are analyzed theoretically. Finally, a critical measure to quantitatively estimate dynamic property of a mechanical assembly process is determined to be assembly coupling dynamic stiffness, on the basis of inverse substructuring dynamic analysis. All analytical results have been validated on a lumped-parameter model set up in this study for two-level of substructures.
2. Substructuring dynamic analysis on mechanical assembly
Dynamic system of a mechanical assembly process can be analyzed by substructuring dynamic analysis with a two-level of substructures A and B shown in Fig. 1. Fig. 1(a) and Fig. 1(b) indicate the dynamic excitation-force (), displacement response (), and representative transfer-function () before assembling and after assembling, named as “FRF at component level” (without subscript ‘’) and “FRF at system level” (with extra subscript ‘’), respectively. Dynamic characteristics of the assembly connector is characterized by “coupling dynamic stiffness ()”. Lowercase , and indicate substructures A, B and their coupling interface, and and represents excitation-force input and displacement-response output, respectively. Thus and , e.g., represent the FRF at component level from the excitation on interface of side-A to the output response also on A, and the FRF at system level from the input excitation on side-B to the output response on A.
Fig. 1Transfer-functions on two-level of substructures before (a) and after (b) mechanical assembling
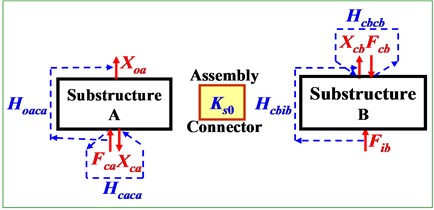
a) FRF at component level
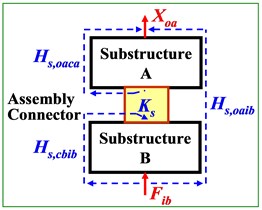
b) FRF at system level
According to substructuring dynamic analysis, the FRFs (e.g. ) can be analyzed and predicted by the FRFs at component level (e.g. , ) together with the known stiffness (). And the relations between the FRFs of a mechanical assembly process can be well explained by following equation [4]:
where:
Symbols +1, −1 for and , and +1, −1 for and , respectively. Eqs. (1) and (2) show that: (1) FRFs at system level (after assembling) can be explicitly expressed by that before assembling, and vice versa; (2) Matrix [], called here as “assembly coupling matrix”, represents dynamic coupling resistance in between components A and B. It characterizes synthetically the dynamic property of a mechanical assembly process; (3) Only the coupling dynamic stiffness [] in [] changes with assembly process. It is generally different from the stiffness [] before assembling.
3. Changes of dynamic characteristics due to assembling process
A mechanical assembly process has affects on dynamic property of either the substructures or the assembly unit system. These affects can be explained by the changes of dynamic characteristics, described by transfer-functions, FRFs, due to assembling. These changes can be described by differences () between FRFs at component level (before assembling) and FRFs at system level (after assembling). For the four representative FRFs before and after assembling, i.e., ( and on A, and on B), and ( and on A, and on B), the differences can be derived from Eqs. (1) and (2), for instances, as follow:
where [] is unit square matrix with the same size of matrix []. Theoretically, since [] [] and , thus Eqs. (3)-(5) show that, the FRFs ( and ) on A after assembling are less than the FRFs ( and ) on A before assembling, and FRF () after assembling is greater than the mathematical product of FRFs () and () before assembling. Similar results can be also obtained for the rest FRFs. That means a mechanical assembly process decreases the transfer-functions of the independent substructures but increases the functional product. Assembling process does change the dynamic characteristics of assembly system. To verify these analytical deductions, here set up a lumped-parameter model, as shown in Table 1 with listed parameters, of the two-level of substructures in Fig. 1.
Table 1Lumped-parameter model for two-level of substructures and its parameters
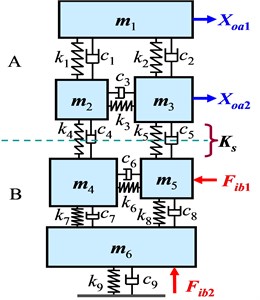 | Mass [kg] | Static stiffness [N/m] | Damping factor [sN/m] | |||
10 | 300 | 15 | ||||
3 | 500 | 20 | ||||
1 | 800 | 6 | ||||
3 | 600 | 5 | ||||
6 | 400 | 10 | ||||
12 | 1000 | 10 | ||||
500 | 25 | |||||
200 | 40 | |||||
1000 | 5 | |||||
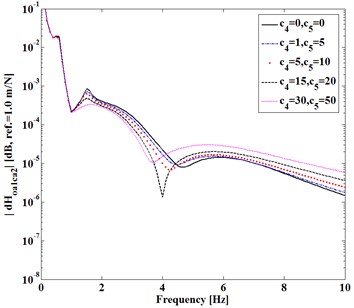
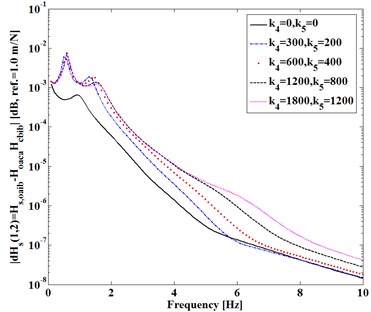
Here consider the first entry (1, 2) of FRF-differences expressed in Eqs. (3)-(5). Fig. 2 shows difference varying with (, ) of and in Fig. 2(a) and with (, ) in Fig. 2(b) as damping factors (, ) and (, ) keep constant, respectively. Fig. 3 shows difference varying with static stiffness (, ) , ). Fig. 4 shows difference as Fig. 2.
Fig. 2Difference |dHoaca(1, 2)| versus Ks
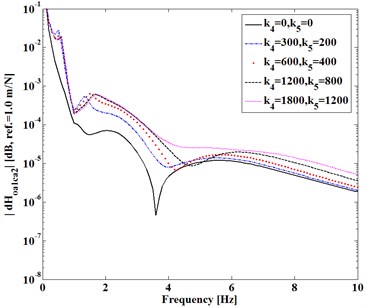
a) Versus (, )
b) Versus (, )
It can be seen from Figs. 2-4 that, (1) Dynamic transfer-functions before assembling have larger magnitudes than that after assembling, because both and are positive; (2) The differences increase with static stiffness of coupling dynamic stiffness []; (3) Dynamic transfer-functions after assembling is larger than the mathematical product of the associated transfer-functions of two substructures before assembling, because of positive (4) Increasing damping factors shows to reduce all the differences near natural frequencies of the assembling substructures and system but increase the differences at higher frequency.
All the trends shown in Figs. 2-4 are consistent with the analytical deductions from Eqs. (3)-(5), which indicate that dynamic characteristics of two independent substructures are explicitly changed by a mechanical assembly process. How to measure these changes due to the assembly is to be discussed next.
Fig. 3Difference |dHcaca(1, 2)| versus (k4, k5)
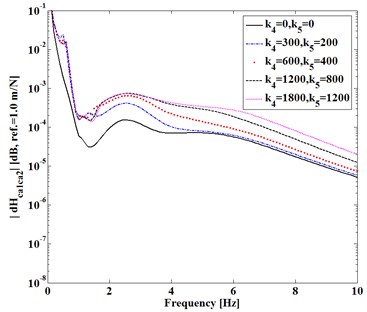
Fig. 4|dHoaib(1, 1)| versus Ks
a) Versus (, )
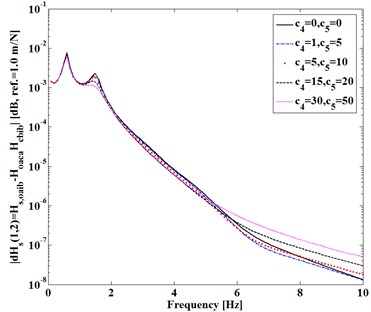
b) Versus (, )
4. Measuring dynamic characteristics changed by mechanical assembly
In fact, dominant factor of dynamic transfer-functions in Eqs. (3)-(5) is coupling dynamic stiffness [] in []. Because matrices [] and [] in [] are FRFs on either sides of substructures A and B before assembling, only [] can be considered as a critical measure of changes of dynamic characteristics due to mechanical assembly. It can be computed by [4]:
From Eq. (6), after testing three FRFs at system level on both sides of A-B interface, [] can be inversely computed. This belongs to “inverse substructuring dynamic analysis”. However in practice, it is often hard to implement tests on assembling interfaces, especially in cases of assembly connector with limited space, which generate non-negligible measurement errors for computing []. Next discuss how to determine [] without the difficulty. If choose the same number of testing points of “excitation-response” on both substructures A and B as that of coupling interface, then from Eq. (5), matrix [] can be derived to be computed by following ‘inverse’ substructuring analysis:
Fig. 5Comparing [Ks] computed by Eqs. (6) and (7) to given ones computed by Eq. (8)
![Comparing [Ks] computed by Eqs. (6) and (7) to given ones computed by Eq. (8)](https://static-01.extrica.com/articles/16294/16294-img9.jpg)
Only if testing four FRFs before assembling, [], [], [] and [], and one FRF after assembling, [], matrix [] can then be computed by either Eq. (7).
Target at the model of Fig. 2, Fig. 5 shows that the two diagonal entries of computed by Eqs. (6) and (7) are exactly the same as the given ones computed by:
where , , and is analytical frequency chosen to be 0-10 Hz.
5. Conclusions
To improve conventional quality inspections and estimations of mechanical assembly, this paper analyzes dynamic characteristics of the assembly process, based on substructuring and inverse substructuring dynamic analysis. Results obtained in this study are concluded as follow:
1) Dynamic transfer-functions of substructures before assembling are greater than that after assembling. While, dynamic transfer-functions of assembly unit system are greater than the product of transfer-functions of substructures before assembling.
2) Assembly coupling dynamic stiffness [] can be used as a critical measure to estimate dynamic characteristics change due to a mechanical assembly process.
3) Using Eqs. (6) and (7) to determine [] based on inverse substructuring analysis are effective. Especially, Eq. (7) developed in this study is more feasible in practical application.
References
-
Xu B. Technical Standards of Mechanical Assembly. China Light Industry Press, 2010.
-
Xiang S. H., Qiu J. B., Wang D. J. The recent progresses on modal analysis and dynamic substructure methods. Advances in Mechanics, Vol. 34, Issue 3, 2004, p. 289-303.
-
Lim T. C., et al. An improved numerical procedure for the coupling of dynamic components using frequency response functions. Proceedings of the 9th International Modal Analysis Conference, Florence, Italy, 1991, p. 902-908.
-
Zhen J. T., Lim T. C., Lu G. Q. Determination of system vibratory response characteristics applying a spectral-based inverse sub-structuring approach, part 1: analytical formulation. International Journal of Vehicle Noise and Vibration, Vol. 1, Issues 1-2, 2004, p. 1-30.
-
Zhen J. T., Lim T. C., Lu G. Q. Determination of system vibratory response characteristics applying a spectral-based inverse sub-structuring approach, part 2: motor vehicle structures. International Journal of Vehicle Noise and Vibration, Vol. 1, Issues 1-2, 2004, p. 31-67.
-
Lu G. G., Wang Z. W. Study on dynamic characteristics of product-packaging-carrier system. Packaging Engineering, Vol. 27, Issue 1, 2006, p. 115-118.
About this article
The authors acknowledge gratefully National Natural Science Foundation of China for supporting research of Projects No. 51475211 and 51205167, including the study of this paper.
