Abstract
A damage identification method was proposed recently, the essence of which resided in locally examining the dynamic equilibrium condition of different structural components under inspection. The singularities of the constructed damage indices were considered to provide effective indication of the location and size of damaged zones. The accuracy of the method, however, suffers from significant interference by measurement noise due to the involvement of high-order derivatives of structural dynamic deflection. Moreover, the applicability of the technique is largely limited, because a variety of baseline parameters of the tested structures, e.g., Young’s modulus and vibration frequencies, must be acquired as prior knowledge. In the present study, continuous wavelet transform (CWT) is first conducted based on the original damage index, yielding enhanced detection results capable of indicating multiple cracks in a beam component. The reliance of the method on the baseline parameters of the tested structure is effectively circumvented by developing a statistical estimation method in the spatial and scale domain, according to which the baseline information can be inversely estimated using only the measured data of structural vibration displacements. As a proof-of-concept investigation, the effectiveness of the newly established damage identification strategy is examined experimentally by identifying multiple cracks in an aluminum beam-like structure.
1. Introduction
Damage is considered as the local reduction or degeneration of the structural geometry of material properties. The occurrence and accumulation of damage seriously jeopardize the safety and efficiency of structural service, and thus timely detection of the existence of damage and evaluation of its severity are considered crucial in both research and engineering fields.
Examination of the changes of structural vibration signatures has proven to have the potential of fulfilling continuous and automated damage evaluation under structural operational states, and has attracted intensive study in recent decades [1, 2]. Changes in a variety of vibration signatures, for example, eigen-frequencies [3-5], mode shape or modal curvature [6-8], electromechanical impedance [9], flexibility matrix [10-12], and damping properties [13], can be well utilized to reflect the feature of damage. Applications of traditional vibration-based methods, however, have been largely hampered mainly because of their reliance on baseline signals captured from previously constructed benchmark structures. Furthermore, the sensitivity of most vibration-based methods to small damage has usually not been satisfactory.
A recently developed damage identification method based on examining the perturbation of structural local dynamic equilibrium was considered to be capable of overcoming the above issues associated with traditional vibration-based techniques, benefiting from its explicit physical implication [14-16]. Specifically, the expression of the damage index was derived based on the equation of motion (EOM) for different types of structural components. Then the location and size of damaged zones can be revealed by observing the singularities of the damage index occurring as a result of change in local dynamic equilibrium. While evincing high sensitivity to damage of small dimensions, particularly to the boundaries of damaged zones, the method also exhibited excessive sensitivity to measurement noise because of the high-order derivatives of vibration displacements involved in the EOM. On the other hand, although the method was free of any baseline signals and benchmark structures, some baseline information was still necessary for constructing the EOMs, namely parameters relating to structural material, geometry, and vibration frequency. Obtaining such information is a challenging, sometimes impossible, task in practical application.
Continuous wavelet transform (CWT) is a powerful tool of signal processing [17-19]. Relying on CWTs, a one-dimensional signal can be translated from the spatial domain to a two-dimensional space-scale domain, from which the scale signals can be interpreted and utilized to achieve various purposes such as singularity identification and noise reduction. In a previous study, CWT was implemented to enhance the noise immunity of the above mentioned damage identification method, and the effectiveness was demonstrated experimentally by identifying a single crack in a beam-like structure [20]. In the present study, multiple cracks were identified using the CWT-enhanced damage index. More importantly, to abolish the dependence of the damage identification method on baseline information that must be measured from an inspected structure, a statistical estimation method was developed based on structural local dynamic equilibrium in the spatial domain. According to this statistical method, optimal estimation of baseline information could be obtained.
As a proof-of-concept investigation, multiple cracks in an aluminum beam-like structure are identified experimentally based on the developed damage identification strategy integrating the implementations of CWT and the statistical estimation method.
2. The original dynamic-equilibrium-based method for damage identification
For an intact Euler-Bernoulli beam component, its EOM can be written as:
where is the vibration displacement of the beam at , , , , and are the Young’s modulus, density, moment of inertia, area of cross-section, and thickness of the beam component in its intact status, respectively; is the angular frequency of the vibration; is the density of external force applied on the component surface.
Without the presence of either damage or external force, Eq. (1) equals zero along the entire beam span because of the satisfaction of dynamic equilibrium. When damage exists, non-zero values will occur at the damaged zones due to the perturbation of equilibrium therein. Moreover, because of the discontinuity in material and geometry at the boundaries of the damaged zone, prominent singularities will be observed at the damage boundaries, according to which the location and size of instances of damage can be accurately identified [15].
Therefore, expression of the one-dimensional damage index (assuming the absence of external force) can be derived based on the left-side term of Eq. (1), as:
where:
It can be seen that by measuring the distribution of structural vibration displacement and the various baseline parameters that are included in , the distribution of the damage index, , can be computed using Eq. (2a), as schematically illustrated in Fig. 1. In a similar way, a two-dimensional damage index can be derived according to classic plate vibration theory.
Fig. 1One-dimensional illustration of the principle of the damage identification method based on the examination of structural dynamic equilibrium conditions
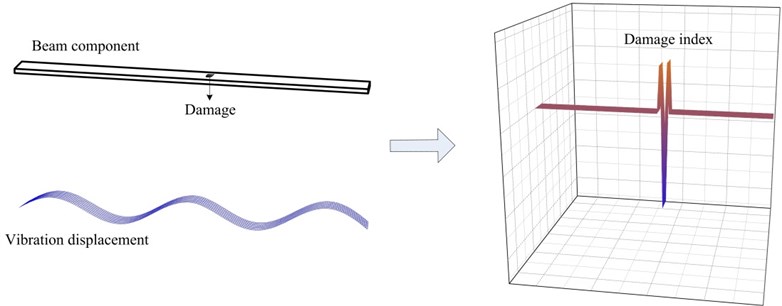
3. Development of the damage identification strategy free of structural baseline information
3.1. Enhanced damage index based on CWT
In ideal cases, in Eq. (2a) shows significant sensitivity to the locations, particularly to the boundaries, of damaged zones. However, because of the noise that cannot be entirely prevented in practical measurement, the identification result can be severely contaminated due to the drastically amplified noise level caused by the fourth-order derivation of vibration displacements included in Eq. (2a). To improve the identification accuracy, CWT is implemented based on Eq. (2a), expressed as:
where is the conjugate of the wavelet function satisfying the condition of ; is the scale parameter; and the asterisk denotes convolution between and , as:
where is the spatial range where the beam is located. According to convolution theorem, Eq. (3a) can be expanded based on Eq. (2a), as:
By using Eq. (3c), the damage index as expressed in Eq. (2a) is extended from the one-dimensional spatial domain to the two-dimensional wavelet domain, i.e., the space-scale domain. In the wavelet domain, the original signal of (in Eq. (2a)) has been decomposed into a series of scale signals. It can be easily understood that in (in Eq. (3c)), the features of measurement noise and the overall trend of the signal are mainly correlated with small and large scales, respectively, whereas the feature of structural damage is associated with intermediate scales and thus can be extracted from the scale spectrum.
3.2. Statistical estimation of structural baseline information
In practical applications, assuming there are measurement points where the vibration displacements are measured, and corresponding to a measurement point where no damage exists, Eq. (3c) becomes:
and can be easily derived to be:
At damaged zones, Eqs. (4a) and (4b) do not hold, and fluctuation of the value of will be seen. Moreover, if the influence of measurement noise is taken into account, will show even more unstable and dramatic variation along the entire beam span. However, it is believed that the values of , although showing large differences from one another, will converge to the exact value of in a statistical manner. To estimate the exact value of under a given scale parameter, the distribution of can be calculated along the beam span using Eq. (4b), the outliers (defined as values that are distant from others and are induced due to a few minimal values of denominator in Eq. (4b), damage, and measurement noise) are excluded from the entire signal and the remaining values are averaged to obtain the estimated .
It is also anticipated that the accuracy of estimating subject to different scales varies because of the different levels of noise influence involved at different scales. Specifically, a larger scale is likely to generate a more accurate estimation of than a smaller scale, since greater noise reduction can be achieved at the larger scale. Therefore, the statistical estimation method should be conducted at different scales to calculate the distribution of over the scale spectrum, from which the optimal estimation of can be ultimately determined.
4. Experimental validation
4.1. Setup
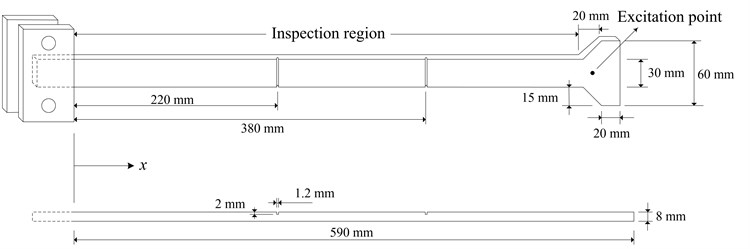
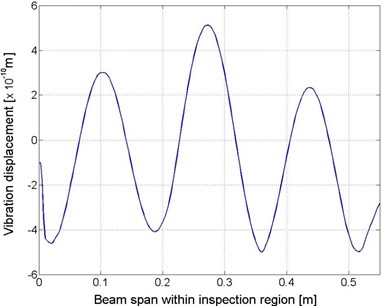
Experimental validation was carried out to evaluate the accuracy of the developed strategy, to identify multiple cracks in a cantilever beam-like structure, as sketched in Fig 2(a). The structure was made of aluminum 6061 with density of 2700 kg/m3 and Young’s modulus of 68.9 GPa. The irregular shape of the structure, i.e., the non-constant width near the free end, was intentionally designed to demonstrate the effectiveness of the strategy subject to complex structural boundary geometries. The defined inspection region, shown in Fig. 2(a), was 550 mm in length, with the constant width of 30 mm and uniform thickness of 8 mm, and contained two through-width cracks (1.2 mm×30 mm×2 mm), each accounting for 0.2 % of the beam span, 220 mm and 380 mm from the clamped end, respectively, as shown in Fig. 2(b). Near the free end of the structure, a harmonic excitation at 2000 Hz was applied on the beam with an electromechanical shaker (B&K®4809). A scanning Doppler laser vibrometer (Polytec®PSV-400B) was used to measure the vibration displacements at 212 measurement points (with a spacing interval of 2.6 mm) along the central line of the beam within the inspection region. The distribution of the vibration displacements is shown in Fig. 3.
Fig. 2a) Schematic of the damaged beam-like structure with multiple cracks, and b) image of the inspection region and the cracks
a)

b)
Fig. 3Distribution of vibration displacements of beam-like structure within the inspection region, subject to vibration frequency of 2000 Hz
4.2. Identification results
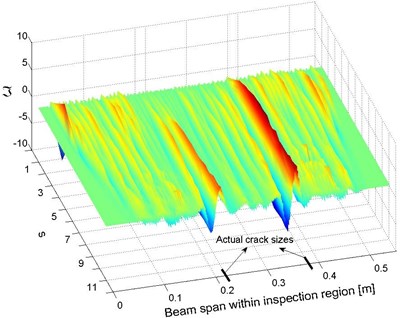
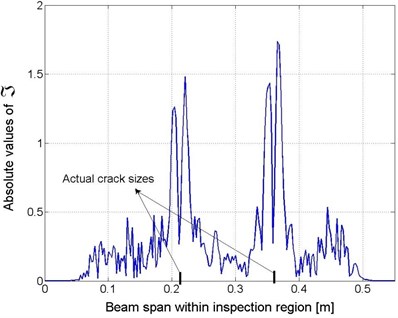
The two cracks were identified using the original method and the newly developed strategy, respectively. As seen from Fig. 4, when Eq. (2a) was applied, the identification result constructed depending on the original method included an excessively high level of noise interference, leading to a severely disturbed signal incapable of providing any information related to damage locations. The detection signal in the space-scale domain, i.e., as expressed in Eq. (3c), was constructed and is shown in Fig. 5(a), where the wavelet function, , was selected to be the first-order derivative of Gaussian function. It is evident that, given a properly selected scale, e.g., , prominent local variations of can be observed at the crack locations. Furthermore, by observing the absolute values of corresponding to , the locations of the cracks can be more clearly identified, as shown in Fig. 5(b).
It should be noted that the identification results shown in Fig. 5(a) and (b) still depended on baseline information from the inspected structure, including the various material and geometric parameters and the vibration frequency, as given in Section 4.1. The statistical estimation method given in Section 3.2 was implemented subsequently, with the aim of eliminating dependence on baseline information. Using the signal corresponding to as an example, the magnitudes of distributed along the beam span, calculated according to Eq. (4b), are shown in Fig. 6. It can be seen from Fig. 6 that the data show dramatic dispersion. Some abnormal values are therefore deemed outliers distributed outside a pre-defined bandwidth, and should be excluded before estimating . Considering the extreme local abnormalities induced due to a few minimal values of the denominator involved in Eq. (4b), as can be recognized from Fig. 6, a narrow bandwidth was set as 10 % of the standard deviation of the entire data, and was estimated as the mean value of the data within the bandwidth.
Fig. 4Result of damage identification based on the original method with damage index constructed using Eq. (2a)
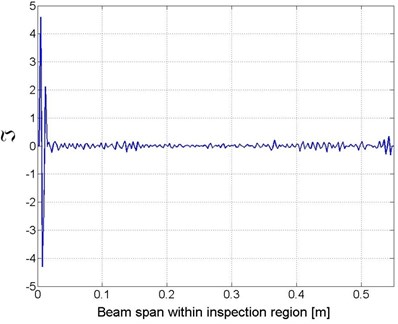
Fig. 5Identification results: a) space-scale domain and b) spatial domain (corresponding to s=11)
a)
b)
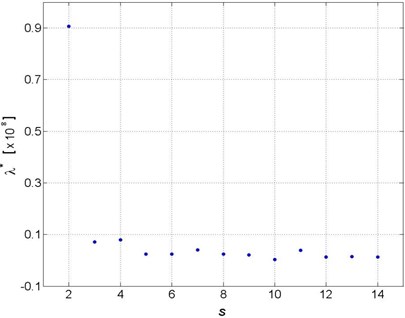
A series of were then estimated at different scales, and the distribution of the estimated is presented over the scale spectrum, from to 14, as shown in Fig. 7. The value of corresponding to was too distant from the other values, and thus is not plotted on the figure. It is obvious that the values of converge to a constant value along with the increase of the scale, because of the increasing reduction of noise influence as explained previously. The optimal was determined by averaging the values between and 15 in Fig. 7, so that the dramatic changes in at small scales, i.e., from to 5, were not taken into account. It was found that the optimally estimated is 2.4 % smaller than the exact value of , which can be easily calculated using the baseline parameters given in Section 4.1.
Fig. 6Distribution of λ * estimated using Eq. (4b) along the beam span subject to s=7
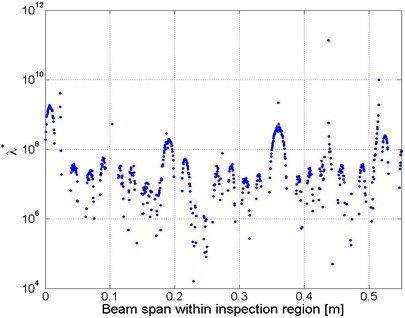
Fig. 7Distribution of estimated λ * over the scale spectrum from s=2 to 14
Relying on the optimal value of , the CWT-based damage index was reconstructed using Eq. (3c), giving rise to the identification results shown in Fig. 8 (a) and (b). It can be seen that the accuracy of the identification results based on the estimated baseline information can be considered equivalent to that relying on prior knowledge of the baseline parameters as shown in Fig. 5(a) and (b).
Fig. 8Identification results: a) space-scale domain and b) spatial domain (corresponding to s=11), constructed with no prior knowledge of structural baseline information
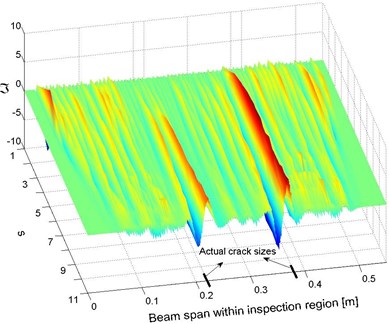
a)
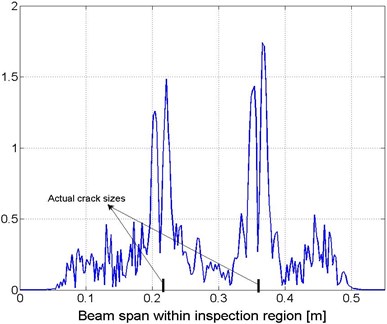
b)
5. Conclusions
CWT was implemented to improve the accuracy of a dynamic-equilibrium-based damage identification method in detecting multiple cracks in a beam-like structure. It was demonstrated by experimental results that, given proper selection of the scale parameter, the features of damage were successfully extracted, revealing the location and approximate size of two cracks. More importantly, a statistical estimation method was developed that eliminate the dependence of the original method on baseline information from the tested structure. The statistical estimation was established based on structural dynamic equilibrium, by integrating the information from spatial and scale domains. The estimation was found to be more stable and accurate associated with relatively large scale parameters, corresponding to which satisfactory noise reduction was achieved. The optimally estimated baseline information was proven to be basically the same as the exact values calculated based on pre-measured structural baseline parameters. When the estimation method was employed, the identification results constructed without baseline information showed equivalent accuracy to the results that depended on prior knowledge of the baseline parameters.
References
-
Farrar C. R., Doebling S. W., Nix D. A. Vibration-based structural damage identification. Philosophical Transactions: Mathematical, Physical and Engineering Sciences, Vol. 359, Issue 1778, p. 131-149.
-
Fan W., Qiao P. Vibration-based damage identification methods: a review and comparative study. Structural Health Monitoring: an International Journal, Vol. 10, Issue 1, 2011, p. 83-111.
-
Salawu O. S. Detection of structural damage through changes in frequency: a review. Engineering Structures, Vol. 19, Issue 9, 1997, p. 718-723.
-
Lee Y. S., Chung M. J. A study on crack detection using eigenfrequency test data. Computers and Structures, Vol. 77, 2000, p. 327-342.
-
Guo H. Y., Li Z. L. A two-stage method for damage detection using frequency responses and statistical theory. Journal of Vibration and Control, Vol. 18, Issue 2, 2011, p. 191-200.
-
Kim J. T., Ryu Y. S., Cho H. M., Stubbs N. Damage identification in beam-type structures: frequency-based method vs. mode-shape-based method. Engineering Structures, Vol. 25, 2003, p. 57-67.
-
Pandey A. K., Biswas M., Samman M. M. Damage detection from changes in curvature mode shapes. Journal of Sound and Vibration, Vol. 145, Issue 2, 1991, p. 321-332.
-
Cao M. S., Ostachowicz W., Bai R. B., Radzienski M. Fractal mechanism for characterizing singularity of mode shape for damage detection. Applied Physics Letters, Vol. 103, 2013, p. 221906.
-
Giurgiutiu V., Rogers C. A. Recent advancements in the electro-mechanical (E/M) impedance method for structural health monitoring and NDE. Proceedings of SPIE on Smart Structures and Materials, Vol. 3329, 1998, p. 536-547.
-
Pandey A. K., Biswas M. Damage detection in structures using changes in flexibility. Journal of Sound and Vibration, Vol. 169, Issue 1, 1994, p. 3-17.
-
Aoki Y., Byon O. Damage detection of CFRP pipes and shells by using localized flexibility method. Advanced Composite Materials, Vol. 10, 2001, p. 189-198.
-
Yan A. M., Golinval J. C. Structural damage localization by combining flexibility and stiffness methods. Engineering Structures, Vol. 27, 2005, p. 1752-1761.
-
Kawiecki G. Modal damping measurement for damage detection. Smart Materials and Structures, Vol. 10, 2001, p. 466-471.
-
Xu H., Cheng L., Su Z., Guyader J.-L. Identification of damage in structural components based on locally perturbed dynamic equilibrium. Journal of Sound and Vibration, Vol. 330, 2011, p. 5963-5981.
-
Xu H., Cheng L., Su Z., Guyader J.-L. Damage visualization based on local dynamic perturbation: theory and application to characterization of multi-damage in a plane structure. Journal of Sound and Vibration, Vol. 332, 2013, p. 3438-3462.
-
Xu H., Cheng L., Su Z., Guyader J.-L., Hamelin P. Reconstructing interfacial force distribution for identification of multi-debonding in steel-reinforced concrete structure using noncontact laser vibrometry. Structural Health Monitoring, Vol. 12, 2013, p. 507-521.
-
Cao M. S., Ostachowicz W., Radzienski M., Xu W. Multiscale shear-strain gradient for detecting delamination in composite laminates. Applied Physics Letters, Vol. 103, 2013, p. 101910.
-
Xu W., Radzieński M., Ostachowicz W., Cao M. S. Damage detection in plates using two-dimensional directional Gaussian wavelets and laser scanned operating deflection shapes. Structural Health Monitoring – An International Journal, Vol. 12, Issue 5-6, 2013, p. 457-468.
-
Cao M. S., Xu H., Bai R. B., Ostachowicz W., Radzieński M., Chen L. Damage characterization in plates using singularity of scale mode shapes. Applied Physics Letters, Vol. 106, 2015, p. 121906.
-
Cao M. S., Cheng L., Su Z., Xu H. A multi-scale pseudo-force model in wavelet domain for identification of damage in structural components. Mechanical Systems and Signal Processing, Vol. 28, 2012, p. 638-659.
About this article
The authors gratefully acknowledge the financial support provided by the Key Program of National Natural Science Foundation of China (Grant No. 11132003), Qing Lan Project and the Fundamental Research Funds for the Central Universities (Grant Nos. 2014B03914 and 2012B05814).
