Abstract
Collapsing vibration caused by demolition blasting of buildings has large effect on the buildings and underground structures nearby. Combined with the demolition blasting of a viaduct, numerical simulation was carried out to investigate dynamic response of subway tunnel subjected to collapsing impact load. The paper put forward composite protective structures of steel-rubber tires and makes safety checking calculation of the subway tunnel on the basis of composite protective measures by numerical simulation. In order to ensure the safety and stability of subway tunnel in the practical operation of demolition blasting of the viaduct, the composite protection system was further optimized, which may provide a good reference for the related engineering practices.
1. Introduction
Demolition blasting technology has a wide range of applications in municipal renovation and expansion project for the advantages of short construction period, low labor intensity and high efficiency. However, due to the relatively small geographical space of urban, demolition blasting brings inevitably a range of negative effects, among which the blasting seismic effect is considered the most serious [1]. The blasting seismic effect can be divided into blasting vibration and collapsing vibration according to the mechanism. A large number of engineering projects show that compared with the blasting vibration the frequency of collapsing vibration is quite similar to the natural frequency of buildings and structures, the amplitude is larger and the duration time is longer. So collapsing vibration of demolition blasting has larger effect on the surrounding buildings and structures than blasting vibration [2, 3]. Especially when the buildings and underground structures are very close to the blasting area, collapsing vibration easily poses a threat to these objectives. Therefore, the collapsing vibration has become a research focus in the effect on the underground structures and buildings nearby.
On the basis of experiments and engineering monitoring researchers studied propagation rule and influence mechanism of collapsing vibration. Zhou studied calculation formula of collapsing vibration velocity caused by blasting demolition [4] and the safe distance of buildings [5]. Wang analyzed the disintegration form of tall buildings, impact energy of tall buildings to the ground and stress wave propagation in the media on the basis of engineering evolution [2]. Tian analyzed the collapsing process of tall buildings in blasting demolishing and some measures of controlling and decreasing collapse vibration were presented [6]. With the deep understanding of the potential hazards of collapsing vibration, dynamic response of buildings and structures should be made qualitative and quantitative analysis, so that the technology of demolition blasting has a more scientific and controlled development. Currently, the seismic design of buildings and structures are studied on the basis of natural earthquake, but collapsing vibration has large difference with structural earthquake in terms of time-frequency characteristic [7]. So they are very necessary to ensure the security and stability of the protected target that making the theoretical analysis and safety assessment of surrounding buildings and structures subjected to collapsing vibration before blasting and making protection and reinforcement of unsafe target.
The paper studied dynamic response of the urban subway tunnel subjected to collapsing vibration of demolition blasting of a viaduct by numerical simulation. And the paper put forward composite protective structures of steel-rubber tires and makes safety checking calculation of the subway tunnel on the basis of composite protective measures by numerical simulation. In order to ensure the safety and stability of subway tunnel in the practical operation of demolition blasting of the viaduct, the composite protection system was further optimized, which may provide a good reference for the related engineering practices.
2. Engineering case
Demolition blasting of the viaduct is an important part of the rapid transformation of main road in a city. The surrounding environment of the main structure of the viaduct is shown in Fig. 1. The subway tunnel crosses under 14# pier of the viaduct and locates 12 meters under the ground. Red portion represents subway tunnel, yellow portion represents the main structure of the viaduct (13#-15# pier). The relative position of the subway tunnel and the viaduct is shown in Fig. 2. The subway tunnel is the key protected object in the demolition blasting project.
Fig. 1The surrounding environment of the viaduct

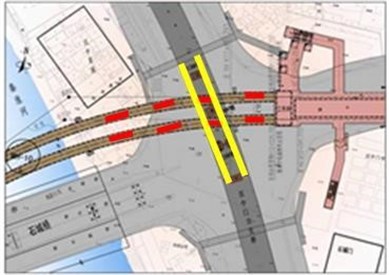
Fig. 2Relative position of subway tunnel and viaduct
3. Numerical simulation without protective measures
3.1. Model
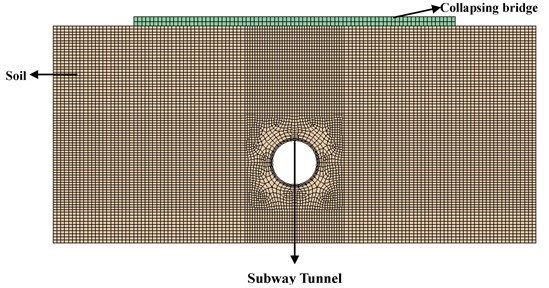
Ground vibration caused by the touchdown of the viaduct is a relatively complex mechanical process. In order to simply the problem, the following assumptions are made for the calculation model established:
1) Soil and concrete materials are continuous and homogeneous isotropic material.
2) The collapsing body of the viaduct impacts the ground vertically in free fall without considering other resistance factors.
The vibration wave generated by parts of the viaduct farther from the subway tunnel had little effect on the subway tunnel, so the study focused on the part of the viaduct above the subway tunnel between 13# pier and 15# pier.
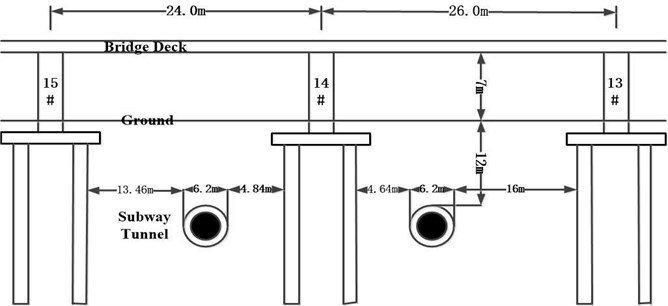
According to the actual size of the viaduct, the bridge model was set to 50 m×20 m×0.6 m, the height from the ground was 7 m. The material of the tunnel lining was C50 concrete and the thickness was 50 cm. The material of the viaduct was C35 concrete. Based on St.Venant principle, it is appropriate to take three times of the size of tunnel face for left and right part of the model to reduce the influence of boundary effects. The normal displacement and rotation of nodes on the symmetry plane were constrained. To further reduce the boundary effect, the calculation model in the left, right and bottom part, the non-reflecting boundary is taken as the boundary. The calculation model was divided into 163030 finite elements and 174106 nodes by Solid3D 164 element and finite element model was shown in Fig. 3.
Fig. 3Calculation model without protective measures
3.2. Material parameters
Constitutive model plays a crucial role in the accuracy of the numerical results. LS-DYNA program has several concrete material models of constitutive relations, such as Soil-and-Foam, Pseudo-Tensor, Oriented-Crack, Geologic-Cap and Concrete-Damage. The paper selected Concrete-Damage constitutive model. Material parameters of C30 and C50 concrete are presented in Table 1 according to the Code for Design on Tunnel of Railway [8]. And material parameters of the soil are presented in Table 2 according to the mechanical properties test of soil sampling. is density, is elastic modulus, is shear modulus, is Poisson ratio, is axial compressive strength, is axial tensile strength, is cohesion, is friction angle.
Table 1Parameters of C30 and C50
Media | (kg/m3) | (GPa) | (GPa) | (N/mm2) | (N/mm2) | |
C30 | 2300 | 31 | 13.3 | 0.2 | 20 | 2.2 |
C50 | 2500 | 35.5 | 15.3 | 0.2 | 33.5 | 3.1 |
Table 2Parameters of soil
Media | (kg/m3) | (MPa) | (MPa) | (KN) | (o) | |
Soil | 1560 | 27.4 | 11 | 0.45 | 20 |
3.3. Analysis and discussion of results
The spreading process of collapsing vibration and dynamic response of subway tunnel were studied by LS-DYNA software. The time of collapsing touchdown of the viaduct is the timing zero point, and the length of computing time was set to 80 ms. The spreading process of collapsing vibration wave in the soil and tunnel lining was shown in Fig. 4 and Fig. 5.
Fig. 4Collapsing vibration wave spreading in the soil

a) 0.2 ms

b) 2.0 ms
c)4.0 ms
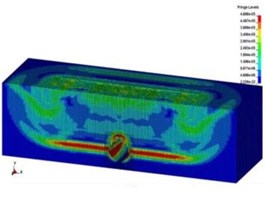
d)7.0 ms
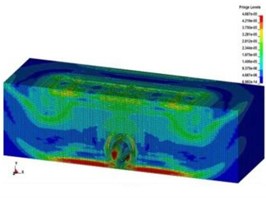
e)9.0 ms
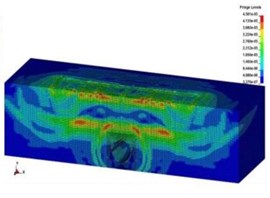
f)14 ms
Fig. 5Collapsing vibration wave spreading in the tunnel lining

a) 1.4 ms
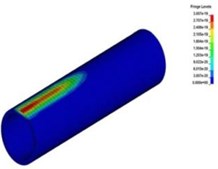
b) 2.8 ms
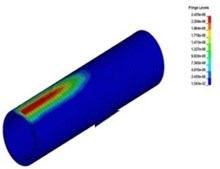
c)4.2 ms
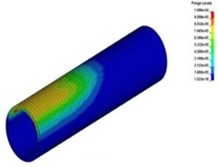
d)5.6 ms
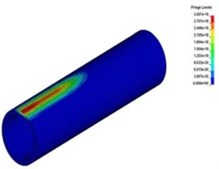
e)7.0 ms
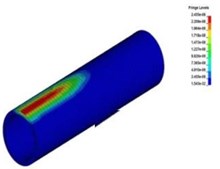
f)8.4 ms
Fig. 6Elements selected in the soil
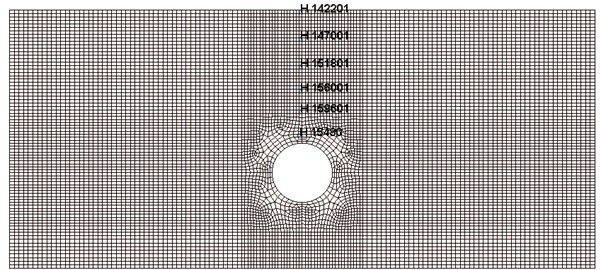
In order to study dynamic response of the soil and tunnel lining more directly, elements of the soil and tunnel lining different depths from the ground surface were selected, as shown in Fig. 6 and Fig. 7. The time-history curves of vibration velocity and stress of the elements were shown in Fig. 8 and Fig. 9.
Fig. 7Elements selected in the tunnel lining
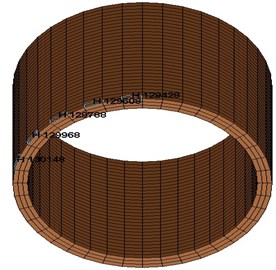
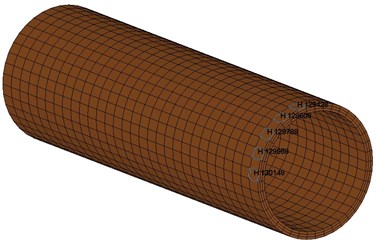
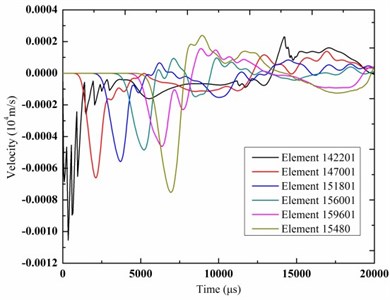
Fig. 8The time-history curves of vibration velocity
a) Soil
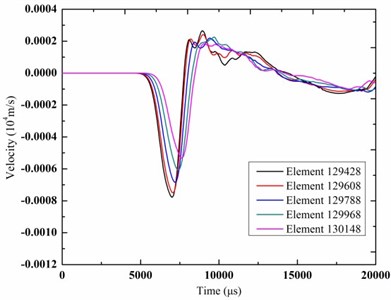
b) Tunnel lining
Fig. 9The time-history curves of stress
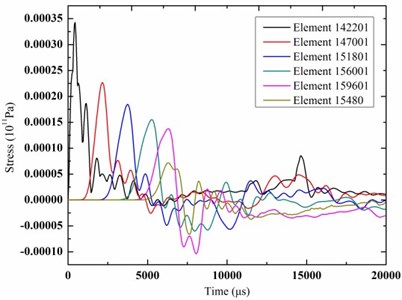
a) Soil
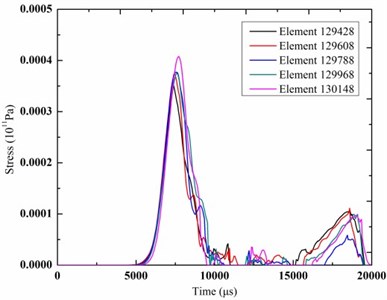
b) Tunnel lining
As shown in Fig. 8, with the depth increasing from the ground surface, the peak vibration velocity of elements in the soil and tunnel lining showed a gradual decreasing trend. The peak vibration of element 15480 was significantly more than element 159601 due to the presence of subway tunnel. The value of vibration velocity of elements increased at first then decreased and gradually reduced to zero. As shown in Fig. 9, with the depth increasing from the surface, the peak stress of elements in the soil showed a gradual decreasing trend, and the peak stress of elements in the tunnel lining showed a gradual increasing trend.
The follow conclusions can be conducted by the numerical simulation:
1) The impact load caused by the collapsing touchdown of the viaduct was firstly acting on the soil and then on the tunnel lining. Due to the radiative decay caused by the increasing wavefront area, absorption attenuation caused by viscous friction of the media and the attenuation caused by the permanent plastic deformation under impact vibration, the stress wave attenuated in the soil.
2) The peak vibration velocity was 7.9 m/s that occurred at the top of the tunnel lining. The peak value of effective stress was 41.6 MPa that occurred at the side of the tunnel lining.
3) In the case of the absence of protective measures, the vibration velocity and effective stress of tunnel lining were very large under the collapsing vibration, which could not meet the requirements of the safety threshold of tunnel lining. The subway tunnel was in the danger. So it was necessary to take measures of shock absorption and protection. For example, cushioning materials was laid on the collapsing area so as to absorb impact energy and reduce stress wave energy.
4. Numerical simulation with protective measures
Numerical results above showed that in the absence of protective measures the impact load caused by collapsing vibration of the viaduct might pose a threat to the stability of subway tunnel. So it was necessary to take measures of shock absorption and protection. The composite protective structure of steel-rubber tires was selected to absorb impact energy and reduce stress wave energy. The numerical simulation of dynamic response of subway tunnel under protective measures was conducted in order to check the damping effect of the protective measures.
4.1. Model
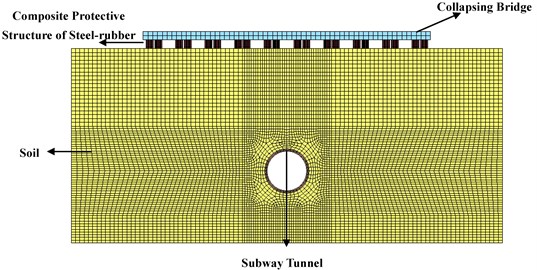
On the basis of the above assumptions the model under the protective measures was shown in Fig. 10. And the local amplification model of the composite protective structure of steel-rubber tires was shown in Fig. 11.
Fig. 10Calculation model of collapsing vibration with protective measures
4.2. Analysis and discussion of results
The time of the viaduct collapsing in contact with rubber tires is the timing zero point, and the length of computing time was set to 80 ms. Fig. 12 showed the spreading process of stress wave in the rubber tires and the deformation process of the rubber tires.
Fig. 11Model of the composite protective structure of steel-rubber tires
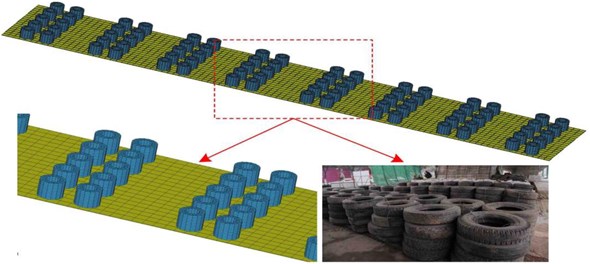
Fig. 12Spreading process of stress wave in the rubber tires and the deformation process of the rubber tires

a)1 ms
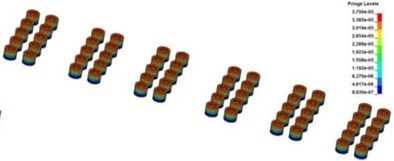
b) 3 ms

c)10 ms

d)25 ms
Fig. 13The spreading process of stress wave in the soil

a) 0.2 ms

b) 2.0 ms
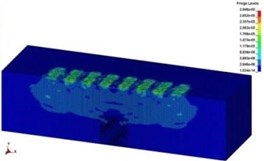
c)4.0 ms
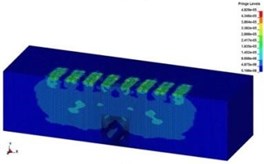
d)7.0 ms
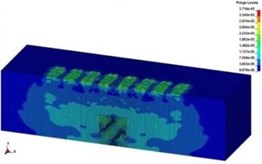
e)9.0 ms

f)14 ms
The deformation of the rubber tires had reached 17.46 cm under the impact at moment 25 ms. Therefore, due to the cushioning effect of the protective structures, the potential energy released by the collapse of the viaduct was partly converted into the deformation energy of rubber tires. Thereby the protective structure could weaken direct impact on the soil. As shown in Fig. 13, due to the buffer action of the composite protective structures, the impact energy of the collapsing body of the viaduct significantly attenuated in the soil in comparison to Fig. 4.
Fig. 14 showed the stress nephogram of tunnel lining. It could be found that the peak stress of tunnel lining from vault to the center of the side wall was lager and the duration was longer than the other parts. The main reason for this phenomenon was caused by the relative position between protective structures and subway tunnel. The more stress energy spreading through two groups of rubber tires above the side wall directly acted on the upper position of the side wall. Therefore, it was very important for the safety and stability of subway tunnel that the relative position between the arrangement of protective structures and subway tunnel were reasonable.
Fig. 14The spreading process of stress wave in the tunnel lining
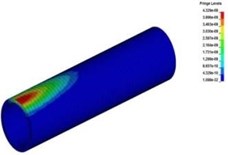
a)6.4 ms
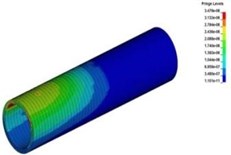
b)9.6 ms
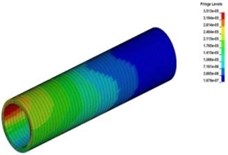
c)12.8 ms
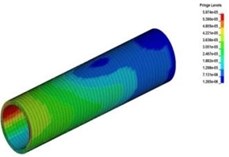
d)20 ms
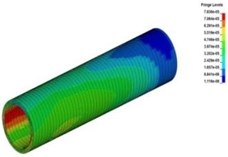
e)36 ms
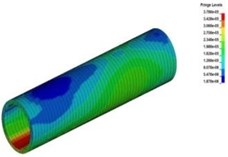
f)52 ms
Fig. 15The time-history curves of vibration velocity of the elements
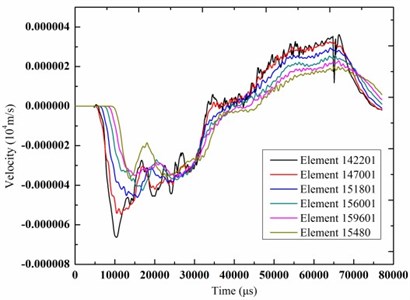
a) Soil
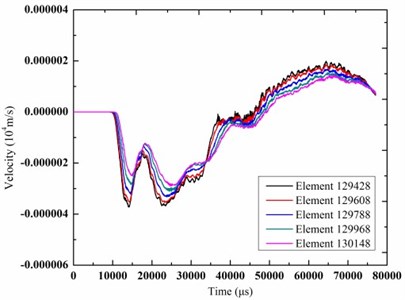
b) Tunnel lining
According to Fig. 6 and Fig. 7, the elements of the soil and tunnel lining at different depths from the ground surface were selected. The time-history curves of vibration velocity and stress were shown in Fig. 15 and Fig. 16.
As can be seen from the results, the rubber tires had a greater deformation and then a rebound phenomenon occurred after the collapsing bridge contacted the cushion that greatly buffed the impact. So the maximal stress of the subway tunnel support layer was only 8.7 KPa that was far below the safety threshold of the subway tunnel. And the maximal vibration velocity was reduced to 0.38 cm/s. The results showed that the cushion had a great damping effect. The stress and the velocity of the soil and the subway tunnel greatly decreased. The reason was that due to the high elastic modulus of the rubber, the vast majority of impact kinetic energy was transformed into the deformation energy of the rubber. So the cushion can play an important role in reducing the collapsing vibration so as to ensure the stability of the subway tunnel.
Fig. 16The time-history curves of stress of the elements
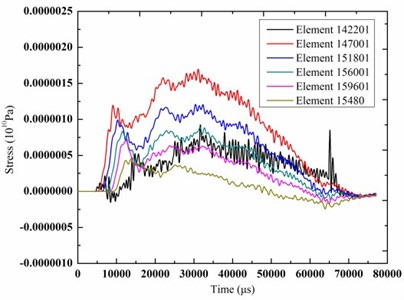
a) Soil
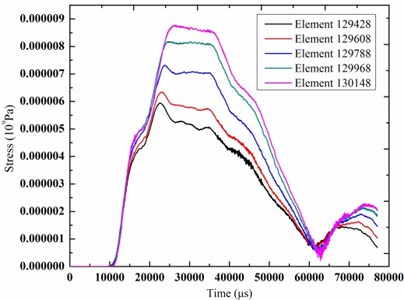
b) Tunnel lining
5. Optimization of protection measures
In order to ensure the safety and stability of subway tunnel in the practical operation of demolition blasting of the viaduct, the composite protection system was further optimized.
The flexible steel frame and sandbag walls were set aside the bridge pier 13# and 15# to reduce the dynamic loads caused by collapsing body of the viaduct. The shock absorber, mild steel damper and the composite protective structures of steel-rubber tires were set aside the bridge pier 14# in order to further attenuate impact energy and vibration load spreading to tunnel lining. The parts of composite protection system were shown in Fig. 17.
Fig. 17The composite protection system of collapsing vibration of the viaduct

a) Flexible steel frame and sandbag walls

b) Shock absorber

c) Mild steel damper

d) Composite protective structures of steel-rubber tires
The monitoring data of subway tunnel in the demolition blasting showed that the peak vibration velocity and the peak stress were respectively 0.45 cm/s and 0.07 MPa, which were smaller than the safety threshold of the subway tunnel. The subway tunnel and internal facilities were intact by the inspection and assessment of the professional sector. Therefore, the protective system had achieved expected effect.
6. Conclusions
Combined with the demolition blasting of the viaduct, numerical simulation was carried out to investigate dynamic response of subway tunnel subjected to collapsing impact load. The paper puts forward composite protective structures of steel-rubber tires and studied the dynamic response of subway tunnel by numerical simulation in comparison to the case without the protective structures. In order to ensure the safety and stability of subway tunnel in the practical operation of demolition blasting of the viaduct, the composite protection system was further optimized. On the basis of the analysis and discussion of the results above, the main conclusions are as follows:
1) In the case of the absence of protective measures, the peak vibration velocity and the peak stress of tunnel lining were very large under the collapsing impact load, which could not meet the requirements of the safety threshold of tunnel lining. The peak vibration velocity of tunnel lining was 7.9 m/s that occurred at the top of the pipe. The peak value of effective stress was 41.6 MPa that occurred in the side wall of tunnel lining. The subway tunnel was in the danger.
2) The composite protective structures could absorb impact energy and reduce stress wave energy to ensure the safety of tunnel structure by the numerical results comparison of two cases. The peak vibration velocity of tunnel lining was 0.38 cm/s that occurred at the vault, the peak effective stress was 8.7 KPa that occurred at the side wall, which reduced by 99.5 % and 99.97 % respectively in comparison with the corresponding values without the protective structures.
3) In order to ensure the safety and stability of subway tunnel in the practical operation of demolition blasting of the viaduct, the composite protection system was further optimized, which included the flexible steel frame, sandbag walls, shock absorber, mild steel damper and the composite protective structures of steel-rubber tires. And the protective system had achieved expected effect by the field monitoring. The peak vibration velocity and the peak stress of tunnel lining were smaller than the safety threshold of the subway tunnel.
References
-
Wang Xuguang, Yu Yalun Demolition blasting technology faced with the 21 century. Engineering Blasting, Vol. 6, Issue 1, 2000, p. 32-35, (in Chinese).
-
Wang Xizhi, Wang Zili, Long Yuan, Xu Quanjun A mathematical model collapse vibration in blasting demolishing tall buildings. Explosion and Shock Waves, Vol. 22, Issue 2, 2002, p. 188-192, (in Chinese).
-
Ye Zhouyuan, Ma Jianjun Harm analysis of collapse touchdown of tower buildings in demolition blasting and its control measures. China Safety Science Journal, Vol. 20, Issue 2, 2010, p. 150-154, (in Chinese).
-
Zhou Jiahan Discussion on calculation formula of collapsing vibration velocity caused by blasting demolition. Engineering Blasting, Vol. 15, Issue 1, 2009, p. 1-4, (in Chinese).
-
Zhou Jiahan, Chen Shanliang, Yang Yezhi, Dai Mingrong Study on the safe distance of vibration caused by blasting demolition. Blasting, Vol. 12, Issue S2, 1993, p. 165-169, (in Chinese).
-
Tian Yunsheng Analysis and control of collapse vibration in blasting demolishing tall buildings. Explosive Materials, Vol. 33, Issue 4, 2004, p. 25-28, (in Chinese).
-
Yao Qiong Safety Analysis of Nearby Building Structure Under Collapse Vibration in Blasting Demolition. Wuhan University of Technology, Wuhan, 2007, (in Chinese).
-
Second Survey and Design Institute of Railways. Code for Design of Railway Engineering – Tunnel, China Railway Press, Beijing, China, 1995.
About this article
We thank the National Natural Science Foundation of China (Grant Nos. 51178460, 11102233, 51304218) for financial support.
