Abstract
Bearings play an important role in mechanical transmission. Many disasters are due to bearing faults. This has driven the need in research for early bearing fault detection. The goal is to extract the periodic impulse signals from the very noise signal which are indicative of a bearing fault. This is done by enhancing impulsive signals while suppressing other signals. This paper used a new method, Narrowband Interference Cancellation, to detect incipient bearing fault. This method filters the narrowband signal not associated with the impulsive signal produced by bearing fault. This improves the signal to noise ratio of impulse train associated with the bearing fault frequency. Finally this methodology is demonstrated on a bearing outer race fault.
1. Introduction
Bearings are critical components in rotating machines, such as helicopter main gearbox, wind turbine gearbox, etc. Therefore they have received a great deal of attention in the field of vibration analysis. In general the vibrations associated with bearing failures are small relative to gear and shaft vibration, making fault detection difficult. Because of this, other methodologies for vibration analysis were needed. When a rolling element strikes a localized defect, an impulse occurs and this excites the resonances of the structure. Envelope analysis is an effective fault diagnosis method which was developed to isolate the defect-induced impulse responses. It is an amplitude demodulation technique based on the high frequency excitation from quasi cyclostationary derived impulses due to bearing component fault. The successful implementation of envelope analysis is dependent on proper selection of the bandwidth window of band-pass filter. Antoni [1] used the spectral kurtosis (SK) to determine the optimum center frequency and bandwidth. Eric et al. [2] quantify the performance of SK and envelope kurtosis (EK) (the kurtosis of envelope prior to estimating the spectrum). Eftekharnejad et al. [3] investigated the comparative effectiveness of applying the Kurtogram to both vibration and AE data from a defective bearing. Zhu et al. [4] used empirical mode decomposition (EMD) to improve the signal to noise ratio. Then envelope analysis was used to identify the bearing fault type. Jiang et al. [5] developed a quantitative bearing fault diagnosis method based on signal complexity and revised morphology filtering. Some pattern recognition methods were also used to diagnose the bearing fault [6]. That said envelope analysis fails if the bandwidth and window are incorrectly selected. In many cases, especially for complex and high capital cost equipment, the test needed to select the proper envelope window is not done. So a more generalized analysis methodology is needed.
As noted, for complex gearboxes (and especially the planetary gearbox), the signals produced by bearing faults will be masked by gear and shaft signal. For bearings the speed of the rolling element which enters the load zone slightly differs from the one that is outside the load zone. This leads to the random fluctuations of bearing signal. So the bearing fault signals are quasi-stationary, while the gears and shafts are deterministic. Recently some methods have been proposed to separate the random signal and deterministic signals. In Wang and Wong [7] and Sawalhi et al. [8], AR model is used to remove the deterministic part of the vibration signal and the AR model residual signal only consists from the random signal (produced by faults). Adaptive noise cancellation (ANC) also has been used to extract the faulty bearing signal from a gearbox system many years ago [9, 10]. In general ANC needs an uncontaminated reference signal that would not be available for most gearboxes where all signals must be transmitted through the gear case. Ho [11] used a delayed version of the primary signal as the reference signal, allowing the separation that can be achieved using one signal only. This procedure is called self-adaptive noise cancellation (SANC), but can suffer from stability issues. Antoni and Randall have also further developed the ANC algorithm [12, 13]. Time synchronous averaging (TSA) as well can be used to separate the gear and bearing signals [14, 15], but it is dependent on stationarity. Bechhoefer et al. developed a narrowband interference cancellation (NIC) method to extract the periodic impulse signals produced by gear faults [16]. The results showed that this method was effective for gear fault detection especially in the planetary gearbox.
Theoretically in a gearbox system, when the bearings have faults but the gears are healthy, the periodic impulsive signals produced by bearing faults can be enhanced by NIC. The signals produced by gears and shafts are narrowband, but the signals produced by bearing faults are broadband, allowing the NIC to remove the synchronous gear tones. Even if the monitored mechanical system only contains bearings and some simple components like shafts, motor and loader, NIC can also enhance the periodic impulsive signals produced by bearing faults. Therefore this paper mainly concentrates on bearing incipient fault detection using NIC.
2. Narrowband interference cancellation
A bearing fault will produce periodic impulse signals with characteristic frequencies which are corrupted by other noise sources, such as shaft rates and various machine components. The vibration signals collected from machines typically contain gear mesh, shaft rotation, bearing vibration and random noise. For the signals produced by gear and shaft, they are narrowband. But the periodic impulse signals generated by bearing faults are in a wide band. Usually the bearing fault signals are very weak compared to the gear mesh tones and shaft rotation. If one can cancel these narrowband signals, the bearing faults will be detectable. A machine system can be modeled as:
where is the signal of interest, is the signal associated with gear mesh, rotation of shafts, e. g. interference, is random noise.
The interference signal is usually large compared to the signal of interest. It is necessary to remove the interfering signal from while preserving the signal of interest . Since the measured signal and the interference signal are correlated, one can estimate the interference using an optimal linear estimator:
Here is an integer delay operator. If , then Eq. (2) is the least square forward linear predictor. If , the output of the filter is . This means we can completely remove the interference and only the desired signal and noise remain. In practice the signal is not available. To overcome this obstacle, we can use a minimum mean square error -step forward linear predictor, such that:
such that:
For this modeling, the components of the observed signal have the following properties:
• The signal of interest , the interference signal , and the noise signal are mutually uncorrelated.
• The noise signal is white.
• The signal of interest is wideband and has a short correlation length (e. g. it is impulsive).
• The interference signal has a long correlation length: its autocorrelation length takes significant values over the range , for . is the correlation length.
In practice the second and third properties mean that the desired signal and the noise are approximately uncorrelated after a certain small lag. These are precisely the properties exploited by the canceller to separate the narrowband interference from the desired signal and the background noise.
According to the first assumption, we have:
If the second and third modeling assumptions hold true, we have:
The exclusion of the lags for in and is critical, and we have arranged for that by forcing the filter and the predictor to form their estimates using the delayed data vector . From Eq. (5), (8) and (11) we conclude that and therefore . Thus the optimum narrowband interference estimator is equal to the -step linear predictor , which can be determined exclusively from the input signal . Then the signal with interference removed is:
which is identical to the -step forward prediction error. This leads to the linear prediction NIC shown in Fig. 1. For a full description of the analysis, we can see reference [17].
Fig. 1Block diagram of linear prediction NBI canceller
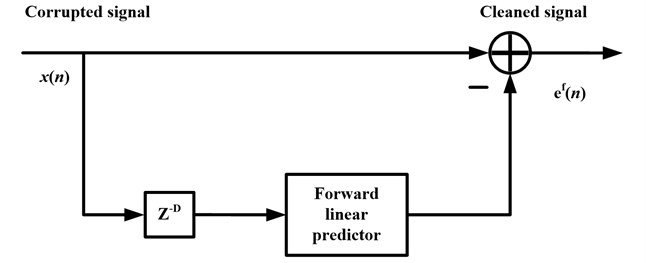
3. Experiment results
The test rig [18] was equipped with a NICE bearing with the following parameters: roller diameter 0.235 inch, pitch diameter 1.245 inch, number of elements is 8, and the contact angle is equal to 0°. The input shaft rotation rate is 25 Hz. The sample frequency is 97,656 Hz and lasting 6 seconds. For baseline and outer race fault conditions, we acquire three data sets respectively under the load 270 lbs. Through the geometric parameters of NICE bearing, the fault characteristic frequencies can be calculated as illustrated in Table 1. And we define the four fault characteristic frequencies as ball pass frequency inner race (BPFI), ball pass frequency outer race (BPFO), ball spin frequency (BSF), and fundamental train frequency (FTF).
Table 1Fault characteristic frequencies at the input frequency of 25 Hz
Type of faults | Fault characteristic frequencies (Hz) |
Outer race fault | 81.12 |
Inner race fault | 118.88 |
Ball fault | 63.86 |
Cage fault | 10.14 |
In this experiment the parameters and of NIC are selected as 1 and 4096. The time domain signals of healthy bearing and of faulty bearing are illustrated as Fig. 2 and Fig. 3.
Fig. 2Time domain signal of healthy bearing
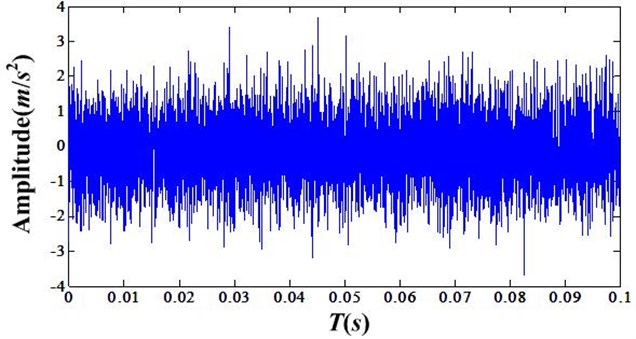
Fig. 3Time domain signal of faulty bearing
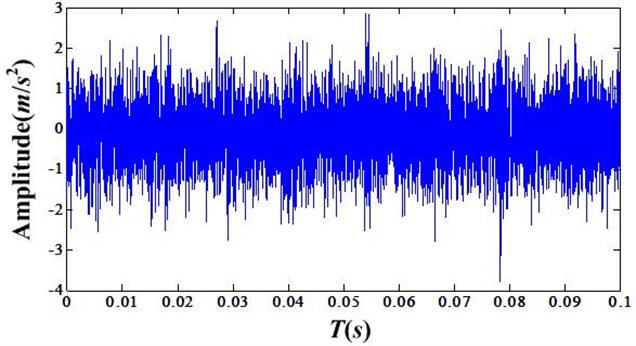
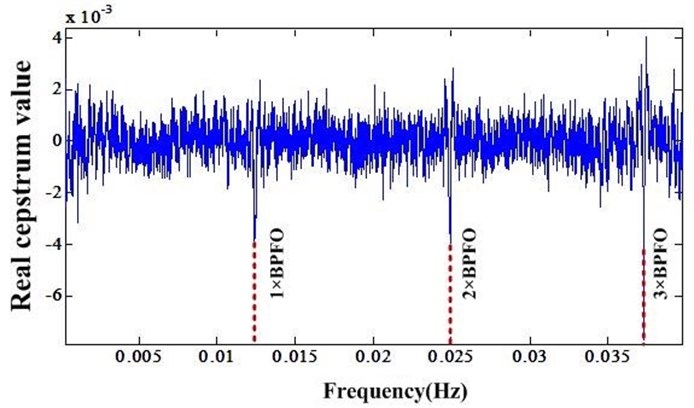
After NIC processing the periodic impulse signal produced by bearing outrace fault can be enhanced. The real cepstrum value of fault bearing can be depicted as Fig. 4. From the Fig. 4 one cannot find any bearing fault information. However after NIC processing, one can easily find the outrace fault frequency as illustrated in Fig. 5.
Fig. 4Cepstrum before NIC processing
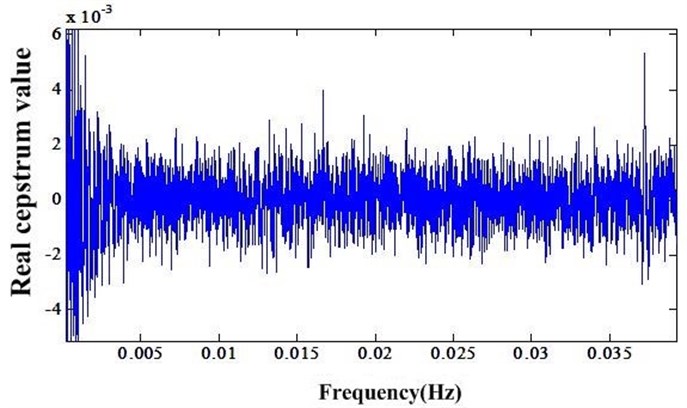
Fig. 5Cepstrum after NIC processing
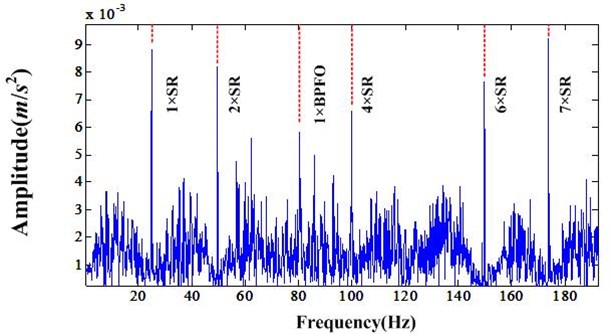
In order to further validate the effectiveness of proposed method, the Fourier transforms of healthy bearing, faulty bearing and faulty bearing after NIC processing were compared. In Fig. 6, the healthy bearing, one can only observe the shaft rate (SR) and its harmonics. In Fig. 7 one can find weak outrace fault frequency, which denotes the faulty bearing. But the amplitude of BPFO is relatively small compared to the SR and its harmonics, which may result in missed detection. After NIC processing the shaft related signals are suppressed and meanwhile the bearing fault signal is enhanced, which can be seen in Fig. 8. Note that the NIC improves the SNR of the BPFO. In summary the NIC method is effective for bearing fault detection, without the need to identify a bearing window needed for envelope analysis.
Fig. 6Fourier transform of healthy bearing
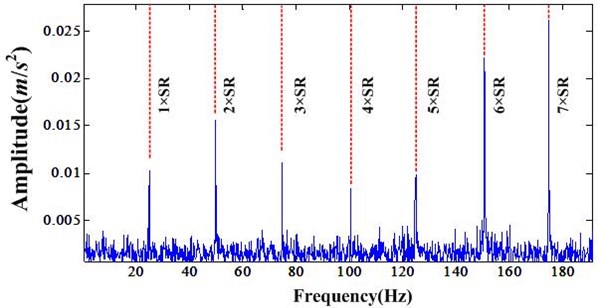
Fig. 7Fourier transform of bearing fault signal
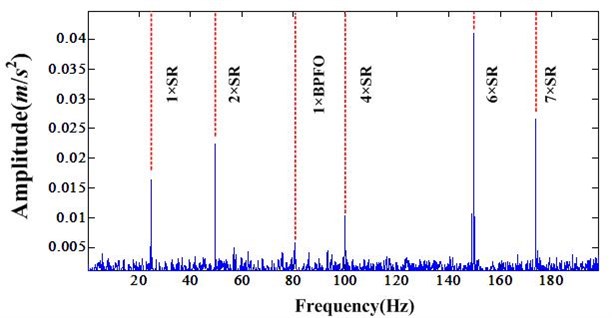
Fig. 8Fourier transform of bearing fault signal after NIC processing
4. Conclusions
This paper used a new method NIC that can enhance the periodic impulse signal produced by bearing fault. For some incipient fault, preprocessing the signal with NIC improves the fault detectability compared to the traditional method like FFT. The NIC was validated on a bearing fault test. However improved performance could possibly be achieved by resampling the time domain signal to correct for changes in shaft rate. This would allow the NIC to remove periodic tones more effectively. Additionally the extraction of condition indicators from the NIC signal needs to be investigated. The condition indicators quantify the magnitude of a fault feature and allow for online/automated condition monitoring. Finally the development of a NIC theory to optimally select the input parameters is needed. Currently this and signal length selection are an ad hock process.
References
-
Antoni J., Randall R. B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines. Mechanical Systems and Signal Processing, Vol. 20, Issue 2, 2006, p. 308-331.
-
Bechhoefer E., Kingsley M., Menon P. Bearing envelope analysis window selection using spectral kurtosis techniques. IEEE Conference on Prognostics and Health Management, Montreal, 2011.
-
Eftekharnejad B., Carrasco M. R., Charnley B., Mba D. The application of spectral kurtosis on acoustic emission and vibrations from a defective bearing. Mechanical Systems and Signal Processing, Vol. 25, Issue 1, 2011, p. 266-284.
-
Zhu K. S., Song X. G., Xue D. X. Incipient fault diagnosis of roller bearings using empirical mode decomposition and correlation coefficient. Journal of Vibroengineering, Vol. 15, Issue 2, 2013, p. 597-609.
-
Jiang K. S., Xu G. H., Liang L., Zhao G. Q., Tao T. F. A quantitative diagnosis method for rolling element bearing using signal complexity and morphology filtering. Journal of Vibroengineering, Vol. 14, Issue 4, 2012, p. 1862-1875.
-
Moosavian A., Ahmadi H., Tabatabaeefar A. Fault diagnosis of main engine journal bearing based on vibration analysis using Fisher linear discriminant, K-nearest neighbor and support vector machine. Journal of Vibroengineering, Vol. 14, Issue 2, 2012, p. 894-906.
-
Wang W., Wong A. K. Autogressive model-based gear fault diagnosis. ASME Transactions, Journal of Vibration and Acoustics, Vol. 124, Issue 2, 2002, p. 172-179.
-
Sawalhi N., Randall R. B., Endo H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis. Mechanical Systems and Signal Processing, Vol. 21, Issue 6, 2007, p. 2616-2633.
-
Chaturvedi G. K., Thomas D. W. Bearing fault detection using adaptive noise cancelling. Journal of Sound and Vibration, Vol. 104, Issue 2, 1982, p. 280-289.
-
Tan C. C., Dawson B. An adaptive noise cancellation approach for condition monitoring of gearbox bearings. Proceedings of the International Tribology Conference, Melbourne, 1987.
-
Ho D. Bearing Diagnostics and Self Adaptive Noise Cancellation. Ph.D. Dissertation, UNSW, 2000.
-
Antoni J., Randall R. B. Unsupervised noise cancellation for vibration signals: Part I – Evaluation of adaptive algorithms. Mechanical Systems and Signal Processing, Vol. 18, Issue 1, 2004, p. 89-101.
-
Antoni J., Randall R. B. Unsupervised noise cancellation for vibration signals: Part II – A novel frequency-domain algorithm. Mechanical Systems and Signal Processing, Vol. 18, Issue 1, 2004, p. 103-117.
-
Klein R., Rudyk E., Masad E., Issacharoff M. Emphasizing bearing tones for prognostics. The International Journal of Condition Monitoring, Vol. 1, Issue 2, 2011, p. 73-78.
-
Klein R., Rudyk E., Masad E., Issacharoff M. Model based approach for identification of gears and bearings failure modes. International Journal of Prognostics and Health Management, Vol. 2, Issue 2, 2011, p. 9.
-
Bechhoefer E., Li R. Y., He D. Quantification of condition indicator performance on a split torque gearbox. Journal of Intelligent Manufacturing, Vol. 23, Issue 2, 2012, p. 213-220.
-
Manolakis D., Ingle V., Kogon S. Statistical and Adaptive Signal Processing. New York, McGraw-Hill, 2000.
-
Fault Data Sets, http://www.mfpt.org/.
About this article
This Project is supported in part by the Chinese Government Research Program under Grant No. 51327020304.
