Abstract
The description of the device with the electrical sensitive glue to fix components of electronic devices (capacitors, resistors, chips) at their trials on harmonic and shock loads with the aid of shaker table is presented. Based on the polarization forces of interaction of the filler particles in the structure of the electrical glue we have performed a simulation and calculation of the limiting values of fixing forces of the component with the electrode of the mounting devices. Parameters of the electric field corresponding to the utmost full transmission of vibrations to the component are determined.
1. Introduction
The most important link in the system to ensure the quality of the transmitted vibration exposures to the object are mounting devices to the source of vibration [1], in particular, to the electrodynamics shaker table [2, 3]. Most of them represent mechanical hardware, based on the use of bolts, brackets, clamps. The main requirement for all types of fasteners is the possibility to ensure a complete transfer of mechanical energy from the shaker table to the test product, which corresponds to the transmission ratio equal to one, over the entire operating range of vibration testing. Most of the known methods of fixing not only do not meet these requirements, but also create additional difficulties in connection with their use for diversified products with different sizes and shapes, that do not allow any damage to the surface.
We have proposed a rapid and economical method of fastening objects by using the electrorheological effect [4, 5], which does not have these drawbacks. A fixing device for fixing parts with the electrical glue [6, 7], when tested in a shaker represents a structural unit, rigidly secured on a table shaker (Fig. 1). To fix the conductive work pieces, it contains an electrode that is used as the metal base of a necessary configuration. A base in the form of alternating plates of electrodes of opposite sign is used to fix work pieces with an insulating coating. A layer of electro-adhesive (electrorheological fluid) [8-10] is located between the work piece and the surface of the mounting block.
Fig. 1Fixing devices for cylindrical capacitors a), flat insulating components b): 1, 2, 4 – base elements, 3 – condensers, 5 – body, 6 – metal plate, 7 – isolator, 8 – ER glue
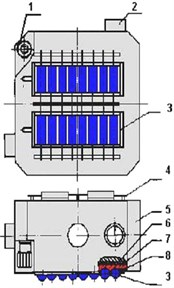
a)

b)
In vibration tests a work piece with the mounting block and a layer of the electrical glue is harmonically vibrated , where – the table offset, – displacement amplitude that is much greater than the layer thickness , – vibration’s frequency. Let us consider the vertical vibrations. In compliance with the regulatory requirements there should not be any resonant oscillations of the detail up to its separation from the substrate-electrode of the mounting device and the transmission coefficient in the amplitude must be kept in magnitude close to one.
The electrical glue is a homogeneous finely dispersed suspension of a dielectric paste that according to its rheological behavior refers to the viscoplastic material having a yield stress. Such materials are characterized by patterns of behavior, characteristic for liquids and for solids, and the degree of their manifestation depends on the value of the external electric impact. Electrorheological dispersions under the influence of the external electric field form a spatial structure of the bridged type of filler particles, oriented along the vector of the field’s intensity. The forces that shape them restrict the movement of the volume elements and give the character of a solid state with an infinitely high viscosity to this material. If the influence of external mechanical forces is smaller than the forces that form the structure, the structures will be deformed elastically [11]. There is a linear proportionality between shear force and deformation. Volume elements with time can be deformed at a rate of relaxation , 0 and nearly instantaneously (10-3 s) recovered [12].
In the structural frame, as shown by visualization of the process, the disappearance of defects of the structure occurs, bridges stretch, and they are supplemented by free particles, therefore resulting in hardening. In this case the irreversible displacement does not occur. Only when external forces reach a value sufficient to overcome the force of the electric interaction between particles – elements of the structure, i.e. they exceed the threshold of the voltage shift, called the yield stress, the bridges will be destroyed, the volume elements of the electrical glue layer can occupy a new position and a solid state will turn into viscoplastic state, and then, with an increase in shear stress – into Newtonian fluid. In the experiments in this case, a sliding of the detail along the surface and its subsequent separation from the electrode mounting hardware of the shaker occurs due to the rupture of the electrical glue layer. To determine the maximum force of vibration impacts that do not violate the integrity of the system “a mounting device – a layer of electrical glue – a work piece”, we consider the structural processes occurring at small shear deformations in the layer of the electrical glue and define the limit of its strength because it is the weakest link in the mechanical system under investigation.
2. Main part
For small displacements the interaction force of the detail and the substrate-electrode of the clamping device through a layer of the electrical glue, is mainly composed of forces of interaction between the particles of independent intact bridges. If their number is , the fraction of intact bonds between particles in a single bridge , the area of a contact between the detail and the electrode base of the mounting device – , – the distance between particles in a structural bridge, then . The dependence of the restoring force of the deformation for one bridge has been identified previously [13, 14] as:
where:
− effective dielectric permittivity of the electrical glue that determines the density of the charge adsorbed at the interface of the particles and dispersion medium as the result of polarization in the electric field.
When intensities are high , → 0, 0.
In Fig. 2 a layer of the electrical glue in between upper plate – the work piece and the lower electrode-the substrate of the mounting device of a shaker table is schematically drawn.
Fig. 2Deformation of the layer of the electrical glue at vertical a) and tangential b) shear
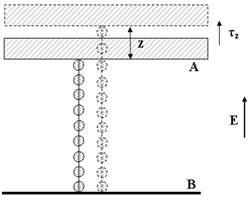
a)
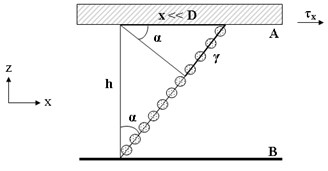
b)
The specific force or the resistance strength to the stretch of the suspension layer along the intensity of the electric field normal to the layer of the electrical glue and electrodes when vertical vibration impact is applied with the consideration of that the bridges’ contact with electrodes in the fraction of of their surface is equal:
It can be explicit through the shift of electrodes , and relative deformation , as:
where: – a particle radius, – the distance, corresponding to the break of the bonds between the particles.
At parallel (tangential) shear of electrodes, the elongation of a bridge that consists of particles, could be expressed through the elongation of the bridge and relative deformation , as , where – angle between the field intensity vector and the bridge, – distance between the particles. The tangential component of force in the tangential shear components can be defined taking in account the relative deformation as:
And similar to the stress of verticle stretching of the electrical glue layer it can be written for the tangential stress:
which reaches the maximum at and higher deformation is lowered – and the flow of the layer of ER-glue begins.
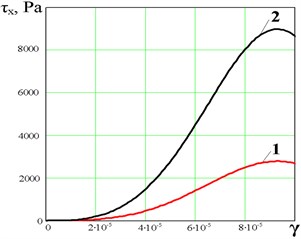
In Fig. 3 typical calculated dependences of the vertical stress a) and tangential stress b) on the values of deformation are shown for the elasto-viscoplastic material (electrical glue on the base of mineral oil and SiO2) in the zone of elastoplasticity.
Fig. 3Elastoplastic characteristic of the ER-glue layer in the electric field by: vertical deformation a): τz0 – zone of linear elasticity, τzm – zone of nonlinear elasticity, τ0 – yield stress; tangential deformation b). E= 1-0.5 kV/mm, 2 – 1 kV/mm
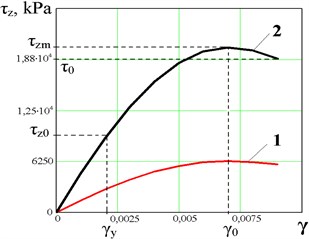
a)
b)
For small vertical deformations , tensile stress is quasi-elastic.
Modulus of elasticity in the vertical extension of the electrical glue layer – a suspension of isolated bridges – is the tension of restoring force resulting from the continuation of the initial linear part of characteristics of the dependence of in the range of deformations 0 – (Fig. 3) up to a single relative strain . In this case the exponent of Eq. (2) and it can be written as:
Elastic limit of ER-suspension of isolated structural bridges in rheology is usually considered a stress of the restoring force at its corresponding relative displacement for which the deviation of the power features of its linear extension is less than the measurement errors, in particular is 0.1 of the value.
Hence, elastic limit is equal to:
Ultimate stress – the tension of the restoring force, corresponding to such state of the medium at which the lattice of the structural bridges that is under the influence of the external mechanical force do not have time to recover in the electric field. In this case processes of hardening do not occur in the layer, the restoring force decreases, and the deformation becomes irreversible and the flow of the suspension starts. From the condition that the ultimate strength is equal to the maximum restoring strain it can be found that . Then, for ultimate stress we have:
Visualization of the processes of creation and destruction of structural frame of the electrical glue has shown that when strain , i.e. specific shear forces are close to ultimate strength a break up of the bridges begins on a mass scale. For a constant load the deformation rate increases, while remaining close to the relaxation rate of the structural lattice. It is restored in the shifted position, a temporary hardening appears and the residual plastic deformation occurs.
When strain , i.e. specific shear forces are higher than the ultimate stress , the deformation rate increases, the hardening process does not occur, a creep occurs and a slow shift (gliding) of a work piece along the electrical glue layer is seen. When strain and a flow for which the stress does not depend on deformation begins.
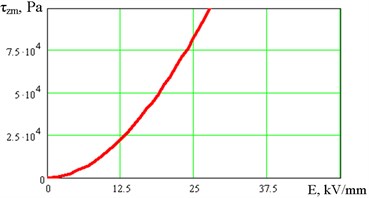
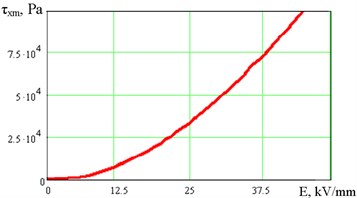
Fig. 4Calculated dependencies of ultimate strength for extension a) and tangential shear b) for electrical glue based on silica and mineral oil
a)
b)
Given the fact that the particles of filler (silica) of the electrical glue have a radius of 10-5m, their specific weight – 2000 kg/m3, the area of their cross-section 3·10-30 m2, the distance between particles in a dense packing, corresponding for electro glue pastes used [7], and the temperature of the experiment we get and the intensity of the field in the interlayer of the dispersion medium corresponding to the beginning of polarization , and 0.5 one can calculate the value of the tensile stress (vertical separation of parts) from the substrate electrode (Fig. 4). It is equal to 100 kPa for a considered dispersion of silica in mineral oil that corresponds to the experimental data previously obtained [12].
As it is seen in Fig. 4 the calculated dependences of the ultimate stress of the structure of the layer of the electrical glue applied between the detail and the substrate-electrode clamping device of the electric field according to (2) for – are parabolic.
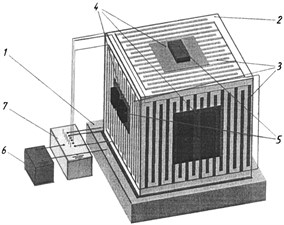
Fig. 5Picture of experimental equipment а) and scheme of electrostatic fixing device b)

a)
b)
To determine the quality of fastening parts to the substrate by means of the electrical glue and to select the optimal modes of electrical impact on it by the dynamic vibration tests, an electrostatic clamping device was used [15], which is installed on a shaker table VEDS 10 A (Fig. 5(a)). In Fig. 5(b) a general view of the electrostatic fixing device is shown. The device comprises a non-conductive substrate made of a solid cube 2 and mounted on the shaker Table 1. The base of the cube is made of an insulating material such as Plexiglas. On all sides of the cube 2 the electrodes 3 are placed at a certain distance one from another and are flushed within its planes. A layer of an electrically sensitive glue 4 with test products 5 is located on all sides of the cube 2. The device is also equipped with a switch 7, designed for fastening products 5 on each side of the cube apart 2 and of the device itself on the shaker table separately.
The switch 7 is connected on one side to a current source 6, and the other – to the electrodes 3 of each of the sides of a cube 2. The width of the electrodes was 2 mm and a dielectric gap between them was also 2 mm. As samples flat capacitors with the aluminum shell and dielectric frames of PCB with chips were used. The contact area of the samples was 12.5 cm2 and their mass m was respectively 54 g and 65.5 g. Amplitude fluctuations of the shaker table and work pieces in the frequency range of 4 to 3000 Hz were measured. Transfer efficiency of mechanical stress is defined as the ratio of output value to the input value of the acceleration of [16].
Fig. 6Dependence of the transmission coefficient of mechanical stress K on the electrical voltage а) and frequency b) for vibrotesting workpieces
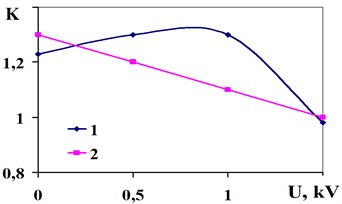
a) Aluminum – 1 and PCB – 2 work pieces
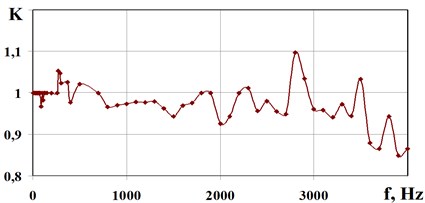
b) PCB work piece, 1.5 kV
In Fig. 6 the dependence of the transmission coefficient of mechanical stress on the resonance frequency of the voltage of the electric field applied to the electrodes of the fastening device for fastening aluminum work pieces and PCB is presented.
When fastening work pieces (65.6 g, 12.5 cm2) and by applying the electric field voltage of 1.5 kV the transmission coefficient 1±10 % is observed in the entire range of frequencies (4-3000 Hz), the dynamic force of separation being 22 kPa.
3. Conclusions
Thus, based on simulation of the behavior of the electrical glue structure at shear stresses in the system of fastening device of the shaker table the values of ultimate strength of the adhesive layer of controlled glue have been estimated by calculations and its dependence on the external electric field is shown. The obtained results allow us to recommend the usage of the fixation method described above on the factories producing complex devices, as it allows one to organize the vibration testing in a more effective way. This result is reached due to the compliance with the main requirement to such fastening devices as to provide the transmission coefficient 1 at mechanical stress by means of its tuning by the external electric field.
References
-
The Tests of Electronics, Electronic Computer Apparatus and Testing Equipment. Ed.` by A. I. Korobov, Moscow, Ratio and Communication, 2002, (in Russian).
-
State Standarts R 53417-2009. Methods of vibration test under constant low frequency.
-
State Standarts 30630.0.0-99. Methods of resistance to external actuating factors test of mechanisms, devices and other technical products.
-
Lykov A. Electrorheological Effect. Minsk, Science and Technology, 1972, (in Russian).
-
Hao T., Kawai A, Ikazaki F. Mechanism of the ER-effect evidence from the conductive, dielectric and surface characterization of water-free ER-fluids. Langmure, Vol. 14, Issue 5, 1998, p. 1256-1262.
-
Shulman Z., Korobko E. Electrorheological Fixing Devices. Minsk, HMTI NAS B, Preprint No. 8, 1991, (in Russian).
-
Korobko E., Kuzmin V., Roisman V., Moroz V. Electrostatic fixing device. Patent BY No. 787. Official Bulletin NCIP, Issue 6, 2012.
-
Quan R., Stech D. Time varying passive vibration absorption for flexible structures. Journal of Vibration and Acoustics, Vol. 118, 1996, p. 36-40.
-
Coquelle E., Bossis G., Szabo D., Giulieri F. Micromechanical analysis of an elastomer filled with particles organized in chain-like structure. Journal of Materials Science, Vol. 41, Issue 18, 2006, p. 5941-5953.
-
Yalcintas M., Dai H. Magnetorheological and electrorheological materials in adaptive structures and Their Performance Comparison. Smart Materials and Structures, Vol. 8, Issue 5, 1999, p. 560-573.
-
Wang B., Rozynek Z., Zhou M., Fossum J. Wide angel scattering study on nanolayered clay/gelatin electrorheological elastomer. Journal of Physics: Conference Series, Vol. 149, 2009, p. 012032.
-
Моkеev A., Korobko E., Vedernikova L. Structural viscosity of electrorheological fluids. Journal of Non-Newtonian Fluid Mechanics, Vol. 42, 1992, p. 213-230.
-
Korobko E. Electrostructuring (electrorheological) fluids: the peculiarities of hydromechanics and their application. Minsk, HMTI NAS B, 1996, (in Russian).
-
Моkеev A., Korobko E. Ultimate strength of electrorheological suspention as a function of electric field intensity. Composite Mechanics and Design, Vol. 2, Issue 1, 1996, p. 97-108.
-
Eschenko L., Kasilovich V., Zhuk G., Korobko E. Study of the mechanism of polarization of activated rheological fluids on the basis of the silicate materials. Proceedings of the 9th Int. Conf. on ERFs and MRS, 2005, p. 124-133.
-
Shirokov A. Reliability of Radioelectronics Devices. Moscow, 1972, (in Russian).
