Abstract
The Direct Torque Control (DTC) technique of Permanent Magnet Synchronous Motor (PMSM) receives increasing attention due to its simplicity and robust dynamic response compared with other control techniques. The classical switching table based DTC presents large flux, torque ripples and more mechanical vibrations in the motor. Several studies have been reported in the literature on classical DTC. However, only limited studies that actually discuss or evaluate the classical DTC. This paper proposes a simple DTC method / Switching table for PMSM, to reduce flux and torque ripples as well as mechanical vibrations. In this paper two DTC schemes are proposed. The six sector and twelve sector methodology is considered in DTC scheme I and DTC scheme II, respectively. In both DTC schemes a simple modification is made in the classical DTC structure that is by eliminating two level inverter available in the classical DTC is replaced by three level Neutral Point Clamped (NPC) inverter. To further improve the performance of the proposed DTC scheme I, the available 27 voltage vectors are allowed to form different groups of voltage vectors such as Large - Zero (LZ), Medium - Zero (MZ) and Small - Zero (SZ), where as in DTC scheme II, all the voltage vectors are considered to form a switching table. Based on these groups, new switching table is proposed. The proposed DTC schemes are comparatively investigated with the classical DTC and existing literatures from the aspects of theory analysis and computer simulations. It can be observed that the proposed techniques can significantly reduce the flux, torque ripples, mechanical vibrations and improves the quality of current waveform compared with traditional and existing methods.
1. Introduction
More or less 40 years ago, in 1971 F. Blaschke proposed the concept of Field Oriented Control (FOC) for Induction Motor [1]. Since, from that time, the FOC dominates in the advanced AC drive market, even though it has complicated structure. Thirteen years later, a new control technique for the Torque Control of Induction Motor was proposed by I. Takahashi and T. Noguchi as Direct Torque Control (DTC) [2]. Two years later M. Depenbrock presented another one control technique named as Direct Self Control (DSC) [3]. The first follows Circular Trajectory and the later follows Hexagon Trajectory. Both of them proved that it is possible to obtain a good dynamic control of the torque without any sensor on the mechanical shaft. Thus, DTC and DSC can be considered as sensorless type control technique.
The DTC scheme normally preferred for low and medium power applications, where as DSC scheme is preferred for high power applications. In this paper, the attention is focused on the DTC scheme, which is best suited for low and medium power applications. The DTC overcomes the drawbacks of FOC such as requirement of current regulators, co-ordinate transformations and PWM signal generators. DTC also provides high efficiency, high power/torque density and high reliability [4-7]. Due to its simplicity, DTC allows a good torque control in steady state and start-up transient state.
On the other hand, the classical DTC have some disadvantages and listed major disadvantages are as follows:
1) difficulty to control torque at very low speed,
2) high current and torque ripple,
3) more mechanical vibrations.
Most of the literature [8-17] surveyed have analyzed classical DTC using two level inverter and all have presented high degree of torque ripple in the results under dynamic conditions and this will reflect in speed and current too. In this paper the possibilities for minimization of torque ripple and mechanical vibrations in the DTC is focused. The minimization of torque ripple is achieved by made improvement in the following areas, such as inverter and switching table.
In this paper the conventional two level inverter is replaced by three level Neutral Point Clamped (NPC) inverter which will have 27 voltage vectors, where as only 8 voltage vectors are available with classical DTC. The 27 voltage vectors include large and medium voltage vectors are six numbers in each, small voltage vectors are twelve numbers and three numbers of zero voltage vectors.
Some of the literature [18-25] presents three level inverter with classical DTC, but it utilizes all the 27 voltage vectors to construct the switching table. This paper proposes three kinds of DTC methods to reduce torque ripple. In the DTC method 1, only the large and zero voltage vectors are used to construct a switching table, where as in DTC method 2, medium and zero voltage vectors alone are utilized to construct a switching table. Small and zero voltage vectors are considered to form a switching table for the DTC method 3.
Thus on the basis of the experience of the authors, the fair comparisons between all the methods are presented in both steady state and external load disturbance / transient conditions. The comparison is useful to indicate to the users which one of the methods can be effectively utilized for various applications that today require torque control.
2. Model of PMSM
2.1. Machine equations
The mathematical model of a PMSM can be expressed as:
and the stator flux equations are:
and the electromagnetic torque developed by a PMSM in a stationary reference frame is expressed as:
or:
2.2. Voltage vector impact on torque
According to principle of DTC, electrical angle between stator and rotor flux vectors can control the torque developed by the PMSM. In background this can be achieved by controlling the voltage vector. Hence the voltage vector is the prime controllable input variable in DTC. However it is mandatory to develop a relation between torque developed and voltage vector.
The voltage and stator flux equations in stationary frame are expressed as:
From Eq. (8) and Eq. (9), we can get:
From Eq. (6), the torque differentiation with respect to time is:
Substituting Eq. (8), Eq. (9) and Eq. (11) in Eq. (12), we can get:
It can be seen from Eq. (13) the equation contains three components [26, 27]. The second component is negative and a function of speed. The third component is also negative and depends on stator resistance. The first component is always positive and depends on voltage vector. From this it is concluded that the non-zero vector always increases the torque developed and the zero vectors always decrease the torque developed.
3. Classical DTC method
Based on the errors between the reference and the actual values of torque and flux, it is possible to control directly the inverter switching states in order to reduce the torque and flux errors within the prefixed band limits. That is why this technique is called as Direct Torque Control. The block diagram of the classical DTC for PMSM is shown in Figure 1.
The basic principle of DTC is to select stator voltage vectors according to the differences between the reference and actual torques. The reference and actual value of the stator flux is processed through two level hysteresis comparator. If the error is positive, the magnitude of flux has to be increased and this is denoted as . If the error is negative, the magnitude of the flux has to be decreased and this is denoted as . The flux comparator conditions are given as:
The rotor reference speed is compared with the actual rotor speed and the error obtained is converted into reference torque by using suitable PI regulator.
The reference and actual torque is processed through three level hysteresis comparator. If the error is positive, the magnitude of torque has to be increased and this is denoted as . If the error is negative, the magnitude of torque has to be decreased and this is denoted as . If the error is zero, the magnitude of torque has to be maintained constant and this is denoted as . The torque comparator conditions are given as:
Fig. 1Block diagram of the classical DTC
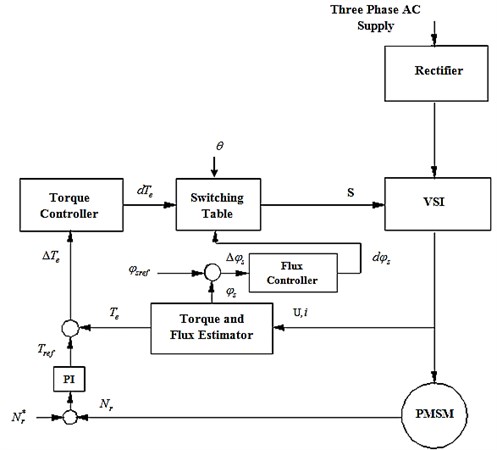
Finally most suitable voltage vectors are selected form the switching table based on the flux and torque errors for all the sectors.
4. Proposed DTC method
The classical DTC uses two level inverter and produces only eight voltage vectors which includes six number of non-zero vectors and rest of them are zero vectors. This does not allow smooth variation in the flux and torque. This could be one of the main reasons for large flux, torque ripples and mechanical vibrations. In this proposed DTC method, the two level inverter is replaced by NPC three level inverter. Due to increment in the level of the inverter there are 27 voltage vectors which are available to construct the switching table. In which six numbers of large vectors, twelve numbers of small vectors, three numbers of zero vectors and remaining are medium vectors.
The inference from the section 3 is that the switching table plays an important role in the DTC technique. For proper switching table the best result can be obtained. The structure of the proposed DTC schemes is shown in Figure 2.
Fig. 2Block diagram of the proposed DTC schemes
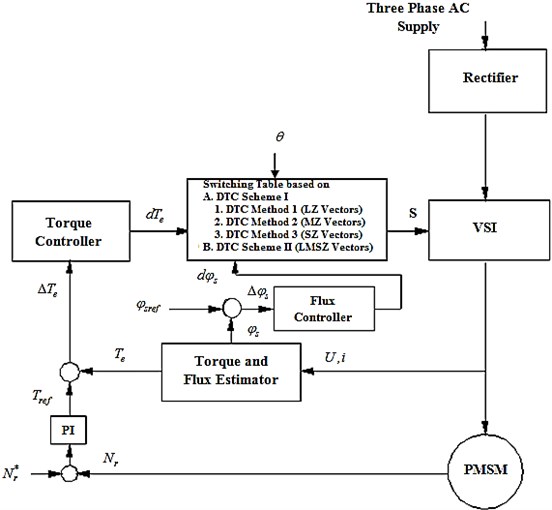
In the proposed DTC scheme I, the available 27 voltage vectors are allowed to form different groups of voltage vectors such as Large - Zero (LZ), Medium - Zero (MZ) and Small - Zero (SZ). Based on these groups, new switching table is proposed. In the proposed DTC scheme II, all the voltage vectors are considered for switching table. The proposed DTC methods provide satisfactory results as compared to classical DTC. The Table 1 provides the technical idea of the proposed DTC schemes.
Table 1Technical difference among the classical and proposed DTC schemes
Proposed DTC scheme I | Proposed DTC scheme II | ||||
Techniques used | Classical DTC | DTC method 1 | DTC method 2 | DTC method 3 | DTC method 4 |
Number of sectors used | Six | Six | Six | Six | Twelve |
Inverter level | Two | Three | Three | Three | Three |
Nature of voltage vectors used | LZ | LZ | MZ | SZ | LMSZ |
4.1. Proposed DTC scheme I
The proposed DTC scheme I includes DTC method 1, DTC method 2 and DTC method 3 and all are following six sector methodology.
4.1.1. DTC method 1
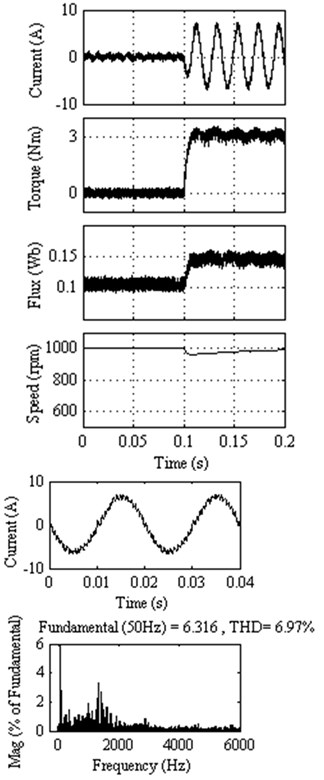
The proposed DTC method 1 utilizes large and zero voltage vectors. In this method 9 voltage vectors are used in which 6 of them are large voltage vectors and 3 of them are zero voltage vectors. This method is almost imitation of the classical DTC, because in both cases only large and zero voltage vectors are used. The switching table is constructed using these 9 voltage vectors. The switching table developed in this method is almost similar to the classical DTC switching table. The drawback obtained in the DTC is repeated in this method also, because of the non availability of intermediate voltage vectors.
4.1.2. DTC method 2
In the proposed DTC method 2, the medium and zero voltage vectors are used to construct switching table. There are 6 medium voltage vectors and 3 zero voltage vectors available. In DTC method 1, the large and zero voltage vectors are used, that means the switching is between large voltage vectors and zero voltage vectors. This will produce large ripples in the flux and torque. However in DTC method 2, the medium and zero voltage vectors are used, so the ripples in the flux and torque are considerably reduced as compared to DTC method 1. This can be observed from Figures 8-12.
4.1.3. DTC method 3
The DTC method 2 produces slightly lesser torque ripples as compared to the classical DTC method. This is because no large voltage vectors are used in this method. From the experience of previous methods, the switching of vector plays important role in the flux and torque ripple reduction. The switching from zero voltage to large / medium voltage increases the ripples in the flux and torque, harmonic content and stress across the switching devices.
To overcome these problems, an appropriate switching table is constructed using only small and zero voltage vectors. The equation (13) tells us that the large voltage vectors are contributing to a torque in the same direction which will lead to large errors in the actual torque. This is true for small voltage vectors also. The lesser torque ripples can be expected by combining small and zero voltage vectors. There are 12 small voltage vectors and 3 zero voltage vectors available in this method. The small voltage vectors exist in redundant pair, i.e. six number of positive small vectors and six number of negative small vectors. So the switching table is formed either by using positive small vector or negative small vector in order to balance neutral point potential. The small voltage vectors are selected to meet the demand of the flux and torque, as well as to reduce the flux, torque ripples and mechanical vibrations. So this ensures the safe operation of the entire system.
4.2. Proposed DTC scheme II
The proposed DTC scheme II is different in the view of number of sectors used and the techniques used in the switching table formation. In this scheme, all the voltage vectors are used to form the switching table. This is referred as DTC method 4 in future.
5. Simulation and results
The MATLAB / Simulink is used to perform the simulation for proposed DTC methods and classical DTC method. The machine parameters used in this paper are the same as in [26, 28] and also the same is listed in Table 2. In this paper the simulation results of classical DTC, DTC method 1, DTC method 2, DTC method 3 and DTC method 4 were presented. For all the methods, the performance analysis was carried out in the different point of view like performance at different operating points, performance during external load disturbance.
Table 2Machine parameters
Number of pole pairs | 3 | |
Permanent magnet flux | 0.1057 Wb | |
Stator resistance | 1.8 Ω | |
-aixs and -axis inductance | 15 mH | |
Rated speed | 2000 rpm | |
Rated torque | 4.5 Nm | |
Rated line-line voltage | 128 V | |
DC bus voltage | 200 V |
5.1. Comparative study with existing work
First, the classical DTC will be carried out to show the effectiveness of the proposed DTC methods. The proposed methods are also compared with existing work [26, 28]. The switching table used in Figure 2 is different from the literature [26, 28].
Figure 3 to Figure 7 present the responses at 1000 rpm with an external load of 3 Nm applied at 0.1 s for classical DTC, DTC method 1, DTC method 2, DTC method 3 and DTC method 4. From the top to bottom, the waveforms are stator current, torque, flux, rotor speed and the harmonic analysis of stator current, respectively. It can be seen that the current waveform is more sinusoidal in the proposed DTC methods as compared to existing methods. The classical DTC exhibits large flux and torque ripples. The Total Harmonic Distortion (THD) is calculated up to 6000 Hz.
The quantitative results are carried out at 1000 rpm with 3 Nm external load for all the methods. It is seen that the stator current THD of the proposed DTC method 3 is 4.40 %, much lower than the 5.85 % and 4.67 % of the existing DTC methods available in the papers [26, 28], respectively. The DTC method 4 provides lesser stator current THD as compared to classical DTC and [26]. Among all the proposed DTC methods and existing DTC methods, the DTC method 3 provides better performance in the view of stator current THD. The dominant harmonics between 2000 Hz and 3000 Hz in proposed DTC method 3 are much lesser than as compared to other proposed methods and classical DTC method.
The average commutation frequency is calculated using the formula, , where is the total commutation instants of all the legs of the inverter used in the DTC methods during fixed period, e.g., 0.05 s in this paper and is the switch numbers.
The Root Mean Square (RMS) torque ripple is calculated for all the DTC methods in this paper. The proposed DTC method 3 exhibits its better performance in terms of torque ripple, stator current THD and average commutation frequency, . The DTC method 3 exhibits better performance while comparing all other proposed methods and classical DTC method.
The average commutation frequency of the proposed DTC method 3 is 1.63 kHz. The proposed DTC method 3 has its average commutation frequency only 51 % and 37 % of that of existing DTC methods available in the literature [26, 28], respectively. This validates the superiority of the proposed DTC methods. The DTC method 4 provides lesser average commutation frequency as compared to [26] where as torque ripple is less while comparing to both [26, 28].
The Table 3 also informs us that all the proposed DTC methods produce lesser torque ripple as compared to classical DTC method. While comparing with the existing DTC methods of [26, 28], the proposed DTC method 3 provides lesser torque ripple. The proposed DTC method 3 gives torque ripple only 54 %, 89 %, 98 % of that of classical DTC method, Zhang et al. [26] and Zhang et al. [28], respectively. The DTC method 4 exhibits lesser torque ripple as compared to classical DTC, [26, 28], DTC method 1 and DTC method 2. In terms of average commutation frequency, torque ripple and THD of stator current, the DTC method 3 shows better performance among all the DTC methods.
Table 3Quantitative comparison of the proposed DTC methods with existing DTC methods
Method | (Hz) | (Wb) | (Nm) | % THD of stator current |
Classical DTC | 5.36 k | 0.0066 | 0.2004 | 6.73 % |
Zhang Y., Zhu J. [26] | 4.41 k | 0.0043 | 0.1222 | 5.85 % |
Zhang Y., Zhu J. [28] | 3.22 k | 0.0017 | 0.1110 | 4.67 % |
Proposed DTC method 1 | 4.99 k | 0.0064 | 0.1956 | 6.97 % |
Proposed DTC method 2 | 4.68 k | 0.0063 | 0.1563 | 5.70 % |
Proposed DTC method 3 | 1.63 k | 0.0048 | 0.1092 | 4.40 % |
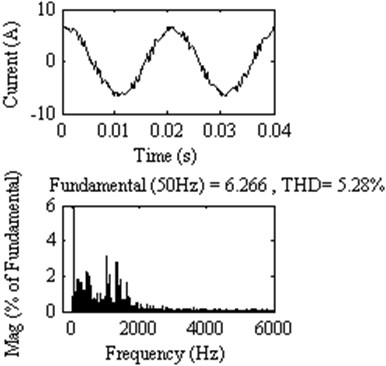
Proposed DTC method 4 | 3.09 k | 0.0086 | 0.1107 | 5.28 % |
Fig. 3Response of classical DTC at 1000 rpm with external load of 3 Nm
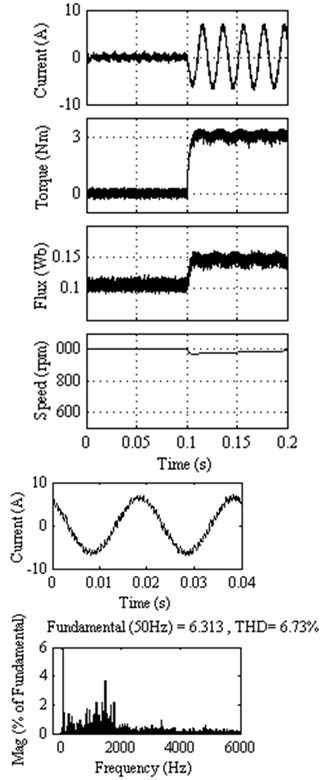
Fig. 4Response of DTC method 1 at 1000 rpm with external load of 3 Nm
5.2. Results at 10 % of rated speed
The proposed DTC methods are analyzed at different operating points. In Figure 8 the operating point is considered at 200 rpm (10 % of the rated speed) without load as an example. Figure 8 shows the flux and torque responses for classical DTC, DTC method 1, DTC method 2, DTC method 3 and DTC method 4, respectively. From top to bottom, the responses shown in Figure 8 are classical DTC, DTC method 1, DTC method 2, DTC method 3 and DTC method 4, respectively, the flux response in the left and torque response in the right.
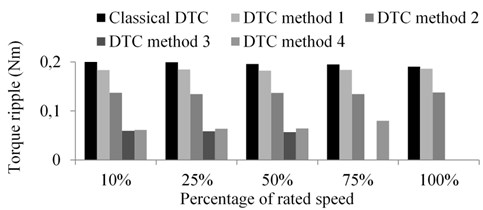
It is seen that for the operating point at 200 rpm, the DTC method 1 gives almost same performance as compared to classical DTC because their switching pattern is almost similar. However the DTC method 2 gives lesser torque ripple as compared to classical DTC and DTC method 1, but gives instantaneous spikes in the flux. The main drawback of the DTC drive is more torque ripple at lower speed. So this analysis provides important conclusion: hence it can be concluded that DTC method 3 presents the best overall performance among the four kinds of proposed DTC methods and classical DTC.
Fig. 5Response of DTC method 2 at 1000 rpm with external load of 3 Nm
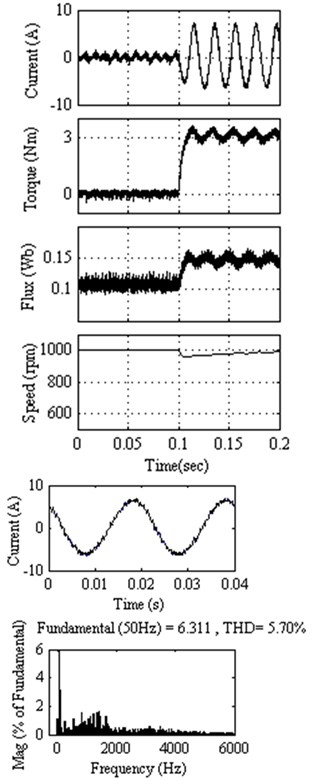
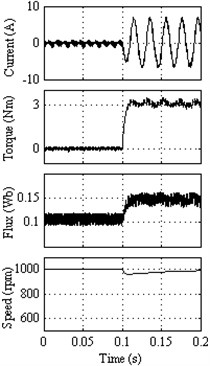
Fig. 6Response of DTC method 3 at 1000 rpm with external load of 3 Nm
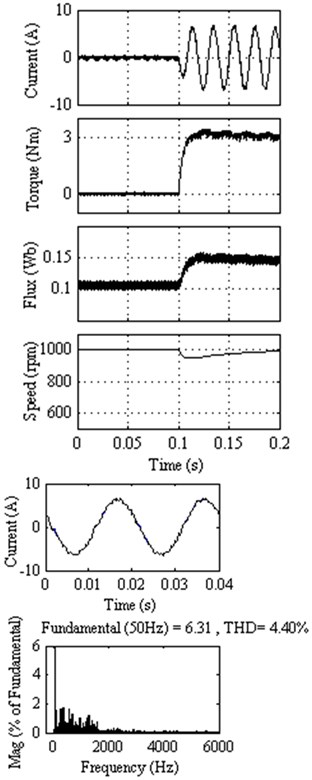
Fig. 7Response of DTC method 4 at 1000 rpm with external load of 3 Nm
a)
b)
Fig. 8Steady state response at 200 rpm (10 % of the rated speed) for classical DTC, DTC method 1, DTC method 2, DTC method 3 and DTC method 4
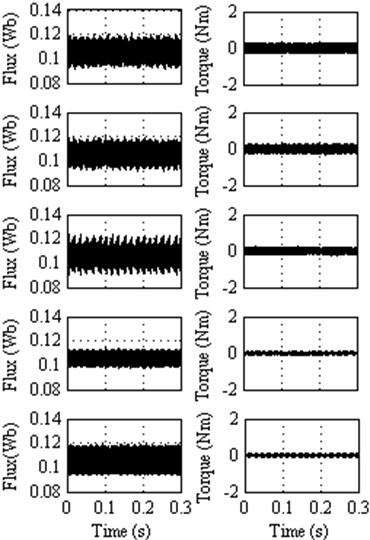
Fig. 9Steady state response at 500 rpm (25 % of the rated speed) for classical DTC, DTC method 1, DTC method 2, DTC method 3 and DTC method 4
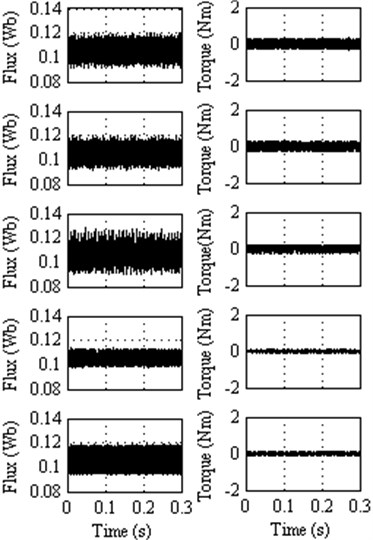
5.3. Results at 25 % of rated speed
At this operating point, in the view of flux and torque ripple, the DTC method 3 exhibits better performance followed by DTC method 4, DTC method 2, DTC method 1 and classical DTC. The ripples in the flux and torque waveform are also significantly diminished in the DTC method 3 as compared to other methods proposed in this paper. This can be observed from the Figure 9.
5.4. Results at 50 % of rated speed
As is shown in Figure 10 the high ripples and distortion in flux and torque waveform can be noticed in all the methods. However, a remarkable reduction in torque ripple can be observed in the DTC method 3. The DTC method 3 and DTC method 4 provide almost similar torque ripple, but the instantaneous spikes are noticed in torque response of DTC method 4.
5.5. Results at 75 % of rated speed
The DTC method 1 almost imitates the classical DTC. The DTC method 2 presents the lower torque ripple among the other methods. According to switching table of this method, at any point of time the inverter will provide half voltages for two lines and zero voltage for one line. This voltage is not sufficient to rotate the rotor at this speed. The DTC method 3 gives satisfactory operation up to 70 % of the rated speed. However the DTC method 4 provides lesser torque ripple compared to all other methods.
5.6. Results at 100 % of rated speed
It is found that there is no significant improvement in the DTC method 1 as compared to classical DTC. Large vectors are considered in classical DTC and DTC method 1. According to equation (13) this will lead to large torque ripples. At the same time, the DTC method 2 presents lesser torque ripple as compared to other methods. Nevertheless the DTC method 3 is not able to trace the reference target.
Fig. 10Steady state response at 1000 rpm (50 % of the rated speed) for classical DTC, DTC method 1, DTC method 2, DTC method 3 and DTC method 4
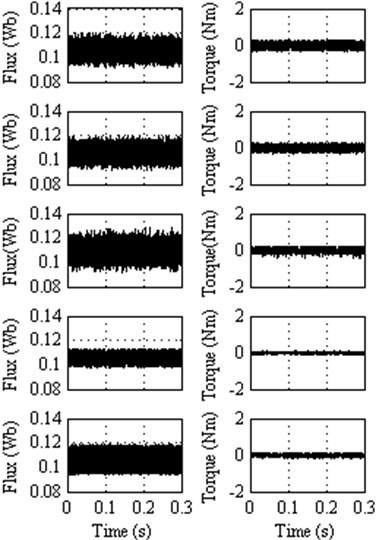
Fig. 11Steady state response at 1500 rpm (75 % of the rated speed) for classical DTC, DTC method 1, DTC method 2 and DTC method 4
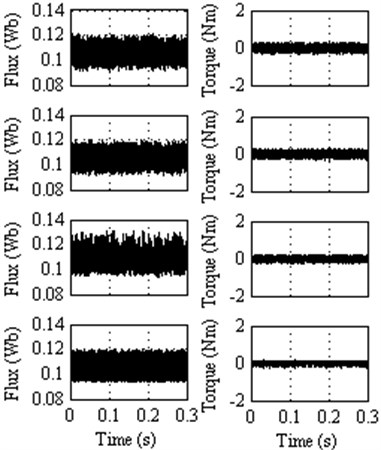
Fig. 12Steady state response at 2000 rpm (100 % of the rated speed) for classical DTC, DTC method 1 and DTC method 2
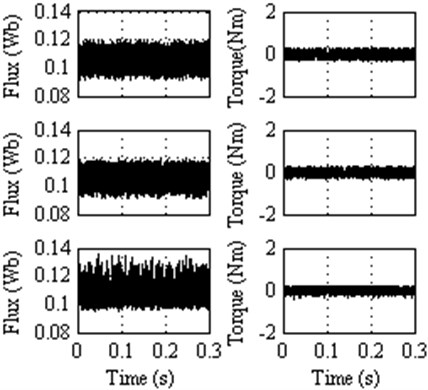
Fig. 13Percentage of rated speed
5.7. Responses to external load disturbance
The responses to the external disturbances are shown in Figure 14(a-e) for classical DTC, DTC method 1, DTC method 2, DTC method 3 and DTC method 4, respectively. The motor is operated at a steady state with 2.5 Nm and 50 % of the rated speed, and then the load is suddenly removed in order to check the disturbance rejection capability of the classical and proposed DTC methods.
In a very short period, the motor speed returns to its original speed due to its fast torque response. It is observed that about 3 % peak speed increases for all the proposed DTC methods 1, 2, 3 and 4, where as it is about 2.5 % for classical DTC method when the load is suddenly removed. However almost all the DTC methods including classical DTC method take the same time to reach its original speed after the load is removed. This comparison informs that all the proposed DTC methods are exhibiting their fast response of torque as compared to classical DTC. Even though the peak speed increases about 3 %, but takes lesser time to reach its steady state, whereas the classical DTC takes the same time to reach from its 2.5 % peak speed. However the classical DTC, DTC method 1 and DTC method 2 exhibit the best performance at the cost of larger torque ripple, whereas DTC method 3 provides lesser torque ripple and better performance in terms of disturbance rejection.
Fig. 14Response to external load disturbance for: a) Classical DTC; (b) DTC method 1, c) DTC method 2, d) DTC method 3, e) DTC method 4
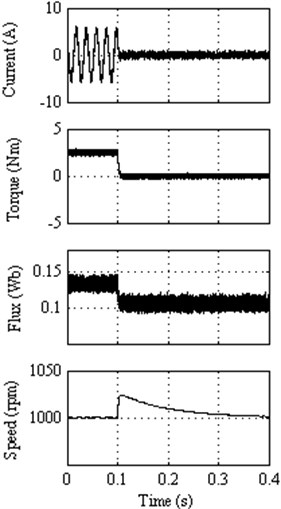
a)
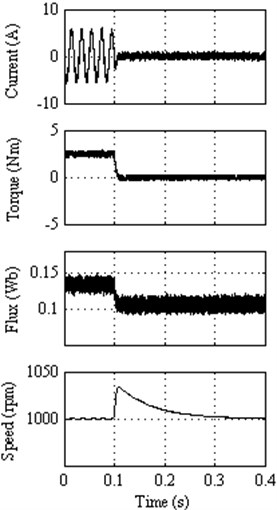
b)
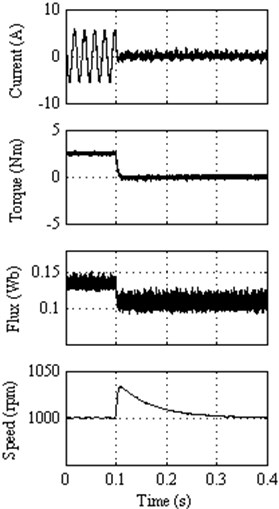
c)
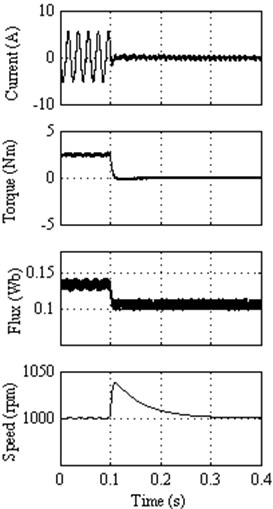
d)
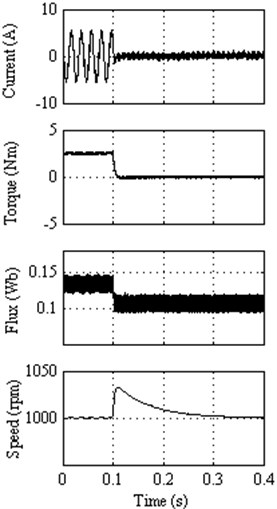
e)
5.8. Harmonics and mechanical vibration reduction
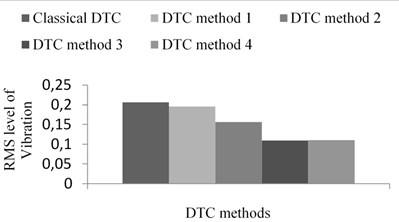
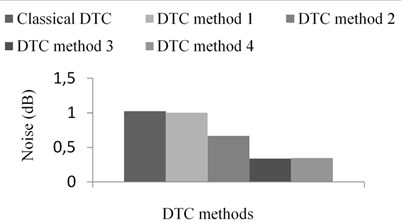
The major disadvantages of the DTC based PMSM drive is more torque ripple and that leads to mechanical vibrations and acoustic noise. For electric and hybrid vehicle applications the torque ripple could result in mechanical vibration and acoustic noise. These phenomenon are undesirable for most of the applications. In this paper the status of the Total Harmonic Distortion in the current waveform, RMS level of vibration and noise have been examined and their comparision is shown in the Figure 15. The RMS level of the vibration is calculated using LabVIEW software. This proves that the proposed DTC methods are able to suppress the torque ripple and mechanical vibration.
Fig. 15Response of DTC methods in the view of mechanical vibration: a) percentage THD of stator current, b) RMS level of vibration, c) noise produced in various DTC methods
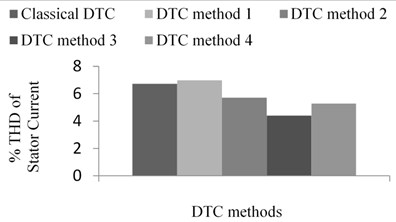
a)
b)
c)
6. Important observations
In this paper the classical DTC method and all the proposed DTC methods are comparatively investigated in the aspect of torque ripple, disturbance rejection performance during external load disturbance and mechanical vibration. From the results indicated earlier, it is found that the torque ripple in the proposed DTC methods is less as compared to classical DTC method and existing literatures. In most of the operating points the proposed DTC method 1 provides slightly higher torque ripple as compared to proposed DTC method 2, 3 and 4. However, proposed DTC method 3 shows better performance in terms of torque ripple as compared to classical DTC method and proposed DTC method 1, 2 and 4. The usage of small and zero voltage vectors in proposed DTC method 3 provides better performance with the comparison of all the methods including classical DTC method. Once again all the DTC methods exhibit all most similar decelerating capability, however proposed DTC method 3 provides lesser ripple in the current waveform. All the proposed and existing DTC methods show good disturbance rejection characteristics at the cost of higher torque ripple except proposed DTC method 3. In the view of mechanical vibration, all the proposed DTC methods provide lesser vibration as compared to classical DTC method.
7. Conclusions
In this paper, a simple method to minimize the torque ripple for a DTC of PMSM drives has been proposed. The new switching table is proposed in which only any two voltage vectors (LZ, MZ and SZ) are utilized out of four voltage vectors (L, M, S, Z) available due to increment in the level of inverter. The performance of the proposed DTC method is comparatively investigated with classical DTC and existing literatures. The simulation results prove that the proposed DTC methods are able to diminish the torque ripple at different operating points as compared to classical DTC. Consequently, the proposed DTC method also gives satisfactory performance during external load disturbance operations. The proposed DTC methods also are capable to suppress mechanical vibration. The settling time of the torque can be reduced if compared with the classical DTC method, furthermore, the related current ripple is also reduced. The proposed DTC methods also retain the merits of simplicity and robustness as in DTC.
References
-
Blaschke F. The principle of field orientation as applied to the new TRANSVECTOR closed loop control system for rotating field machines. Siemens Rev., Vol. 34, 1972, p. 217-220.
-
Takahashi I., Nogushi T. A new quick-response and high efficiency control strategy of an induction motor. IEEE Trans. Ind. Appl., Vol. IA-22, No. 5, Sep. 1986, p. 820-827.
-
Depenbrock M. Direct self-control (DSC) of inverter-fed induction machine. IEEE Trans. Power Electron., Vol. 3, No. 4, Oct. 1988, p. 420-429.
-
Cheng B., Tesch T. R. Torque feed forward control technique for permanent-magnet synchronous motors. IEEE Trans. Ind. Electron., Vol. 57, No. 3, Mar. 2010, p. 969-974.
-
Tursini M., Chiricozzi E., Petrella R. Feed forward flux-weakening control of surface-mounted permanent-magnet synchronous motors accounting for resistive voltage drop. IEEE Trans. Ind. Electron., Vol. 57, No. 1, Jan. 2010, p. 440-448.
-
Ortega C., Arias A., Caruana C., Balcells J., Asher G. M. Improved waveform quality in the direct torque control of matrix-converter-fed PMSM drives. IEEE Trans. Ind. Electron., Vol. 57, No. 6, Jun. 2010, p. 2101-2110.
-
Foo F., Rahman M. F. Sensorless sliding-mode MTPA control of an IPM synchronous motor drive using a sliding-mode observer and HF signal injection. IEEE Trans. Ind. Electron., Vol. 57, No. 4, Apr. 2010, p. 1270-1278.
-
Buja G. S., Kazmierkowski M. P. Direct torque control of PWM inverter-fed AC motors – a survey. IEEE Trans. Ind. Electron., Vol. 51, No. 4, Aug. 2004, p. 744-757.
-
Zhong L., Rahman M. F., Hu W., Lim K. Analysis of direct torque control in permanent magnet synchronous motor drives. IEEE Trans. Power Electron., Vol. 12, No. 3, May 1997, p. 528-536.
-
Foo G., Rahman M. F. Sensorless direct torque and flux-controlled IPM synchronous motor drive at very low speed without signal injection. IEEE Trans. Ind. Electron., Vol. 57, No. 1, Jan. 2010, p. 395-403.
-
Pacas M., Weber J. Predictive direct torque control for the PM synchronous machine. IEEE Trans. Ind. Electron., Vol. 52, No. 5, Oct. 2005, p. 1350-1356.
-
Kang J. K., Sul S. K. New direct torque control of induction motor for minimum torque ripple and constant switching frequency. IEEE Trans. Ind. Appl., Vol. 35, No. 5, Sep./Oct. 1999, p. 1076-1082.
-
Abad G., Rodriguez M. A., Poza J. Two-level VSC based predictive direct torque control of the doubly fed induction machine with reduced torque and flux ripples at low constant switching frequency. IEEE Trans. Power Electron., Vol. 23, No. 3, May 2008, p. 1050-1061.
-
Romeral L., Arias A., Aldabas E., Jayne M. Novel direct torque control (DTC) scheme with fuzzy adaptive torque-ripple reduction. IEEE Trans. Ind. Electron., Vol. 50, No. 3, Jun. 2003, p. 487-492.
-
Morales Caporal R., Pacas M. Encoderless predictive direct torque control for synchronous reluctance machines at very low and zero speed. IEEE Trans. Ind. Electron., Vol. 55, No. 12, Dec. 2008, p. 4408-4416.
-
Shyu K. K., Lin J. K., Pham V. T., Yang M. J., Wang T. W. Global minimum torque ripple design for direct torque control of induction motor drives. IEEE Trans. Ind. Electron., Vol. 57, No. 9, Sep. 2010, p. 3148-3156.
-
Flach E., Hoffmann R., Mutschler P. Direct mean torque control of an induction motor. Proc. EPE, Vol. 3, 1997, p. 672-677.
-
Andreescu G. D., Pitic C., Blaabjerg F., Boldea I. Combined flux observer with signal injection enhancement for wide speed range sensorless direct torque control of IPMSM drives. IEEE Trans. Energy Convers., Vol. 23, No. 2, Jun. 2008, p. 393-402.
-
Zhang Y., Zhao Z., Lu T., Yuan L. Sensorless 3-level inverter-fed induction motor drive based on indirect torque control. Proc. IEEE 6th IPEMC Conf., 2009, p. 589-593.
-
Tang L., Zhong L., Rahman M. F., Hu Y. A novel direct torque controlled interior permanent magnet synchronous machine drive with low ripple in flux and torque and fixed switching frequency. IEEE Trans. Power Electron., Vol. 19, No. 2, Mar. 2004, p. 346-354.
-
Casadei D., Profumo F., Serra G., Tani A. FOC and DTC: two viable schemes for induction motors torque control. IEEE Trans. Power Electron., Vol. 17, No. 5, Sep. 2002, p. 779-787.
-
Kouro S., Bernal R., Miranda H., Silva C., Rodriguez J. High performance torque and flux control for multilevel inverter fed induction motors. IEEE Trans. Power Electron., Vol. 22, No. 6, Nov. 2007, p. 2116-2123.
-
Lee K. B., Blaabjerg F. An improved DTC-SVM method for sensorless matrix converter drives using an overmodulation strategy and a simple nonlinearity compensation. IEEE Trans. Ind. Electron., Vol. 54, No. 6, Dec. 2007, p. 3155-3166.
-
Zhang Y., Zhu J., Zhao Z., Xu W., Drroell D. G. An improved direct torque control for three-level inverter-fed induction motor sensorless drive. IEEE Trans. Power Electron., Vol. 27, No. 3, Mar. 2012, p. 1502-1513.
-
Zhang Y., Zhu J., Xu W. Predictive torque control of permanent magnet synchronous motor drive with reduced switching frequency. Proc. Int. Conf. Electr. Mach. Syst., 2010, p. 798-803.
-
Zhang Y., Zhu J. Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency. IEEE Trans. Power Electron., Vol. 26, No. 1, Jan. 2011, p. 235-248.
-
Zhang Y., Zhu J., Xu W., Guo Y. A simple method to reduce torque ripple in direct torque-controlled permanent-magnet synchronous motor by using vectors with variable amplitude and angle. IEEE Trans. Ind. Electron., Vol. 58, No. 7, 2011, p. 2848-2859.
-
Zhang Y., Zhu J. A novel duty cycle control strategy to reduce both torque and flux ripples for DTC of permanent magnet synchronous motor drives with switching frequency reduction. IEEE Trans. Power Electron., Vol. 26, No. 10, Oct. 2011, p. 3055-3067.
