Abstract
Mobile phones can be used as potential useful tool in structural modal identification. Using the acceleration data collected by mobile phone sensors under ambient excitation, a method for structural modal identification based on variational mode decomposition (VMD) is proposed. Firstly, the feasibility and applicability of mobile phone sensors for vibration data measuring is verified by a shaking table test of a steel frame structure. Then, the mobile phone is used as an accelerometer to record the vibration acceleration of a pedestrian overpass under ambient excitation. In this test, vibration acceleration is effectively decomposed by VMD, and the major components of the vibration signal is obtained through the division and screening of frequency domain. Finally, the modal parameters of the pedestrian overpass are identified, and the results show the identification method based on VMD is effective and feasible.
Highlights
- The feasibility and applicability of mobile phone sensors for vibration data measuring is verified by a shaking table test of a steel frame structure.
- Using the acceleration data collected by mobile phone sensors under ambient excitation, a method for structural modal identification based on variational mode decomposition (VMD) is proposed.
- The signal is interpolated before VMD to reduce the error caused by asynchronous sampling.
- The frequency domain method is used for modal identification of the pedestrian overpass in this paper. The procedure of the identification consists two steps, i.e., (1) identification of the natural frequency, and (2) identification of the mode shapes.
- To verify the accuracy of the identification results, the numerical model of the tested structure is established for comparative analysis.
1. Introduction
Structural dynamic identification is an important means of damage detection and health monitoring, and it has application prospect in automatic modal parameter extraction techniques [1]. However, there exist several problems at present, e.g., 1) the number of channels for data acquisition equipment is limited, 2) proprietary sensors and data acquisition equipment cost high and 3) installation and commissioning processes are complex and time-consuming. Many wireless accelerometer system and data network have been developed to solve above problems [2, 3], and the mobile sensors are also widely used in dynamic identification [4]. As a simple wireless device with accelerometer, mobile phone has potential in dynamic detection, which can realize real-time, efficient, simple, and low-cost detection of structure. In this paper, the feasibility and applicability of structural dynamic identification based on mobile phone sensors are studied. We compare the accuracy and precision between the collected data from mobile phone sensors and professional sensors installed for a shaking table test to verify the feasibility of mobile phone as an accelerometer [2]. Then, the pedestrian overpass was tested based on the mobile phone sensor under ambient excitation, and the modal parameters are identified. During this process, the acceleration data was interpolated [5-7], and then the data was processed based on VMD to improve the accuracy of identification [8]. Finally, the identification results are compared with the theoretical results, to verify the effectiveness of the data processing method based on VMD and the applicability of structural modal identification based on mobile phone sensor.
2. Verification of accuracy and reliability of mobile phone sensor data
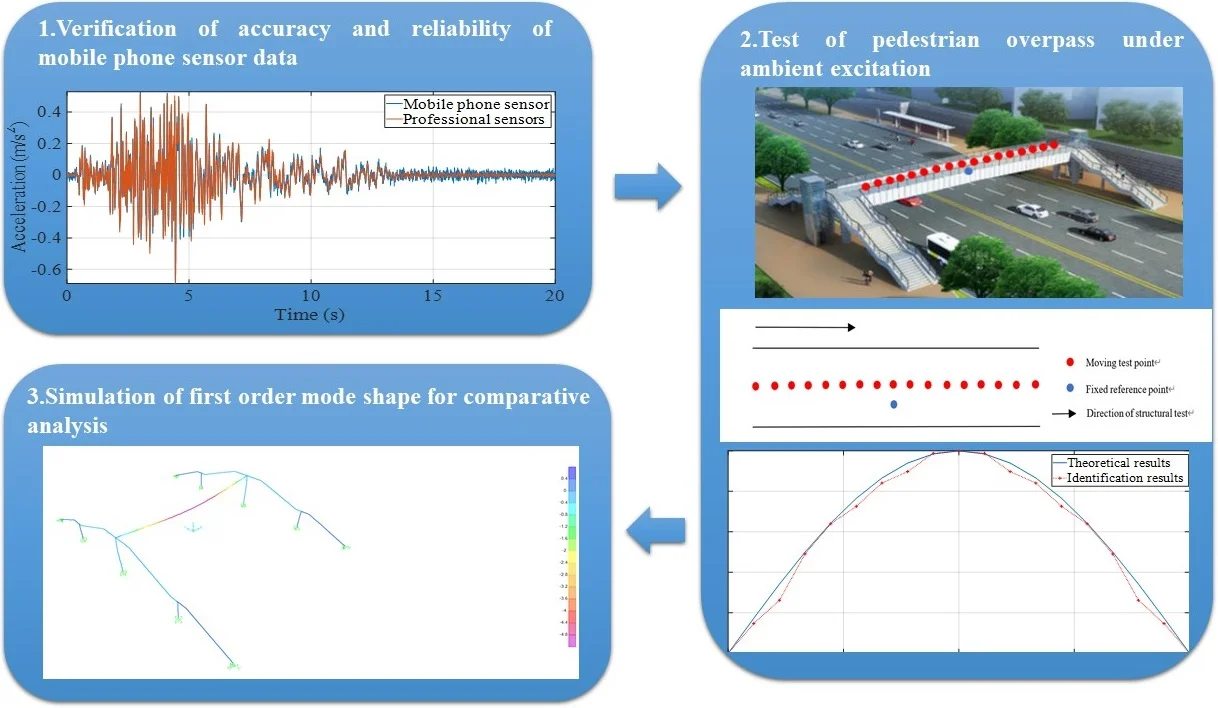
The structure and sensor arrangement of the shaking table test is shown in Fig. 1. The acceleration time histories of base slab of the structure seismic excitation recorded using mobile sensors and professional sensors are presented in Fig. 2, and the corresponding response spectra and power spectra are given in Figs. 3 and 4. It can be found that the time history curves are close, indicating that the data of both types of sensors are in good agreement. As shown in Figs. 3-4, the spectrum analysis results of both sensors are also close, which verifies the accuracy and reliability of the data from mobile phone sensors.
Fig. 1Structure and sensor arrangement of the shaking table test

Fig. 2Acceleration time history curves
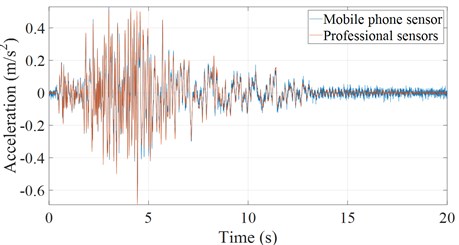
Fig. 3Acceleration response spectrum
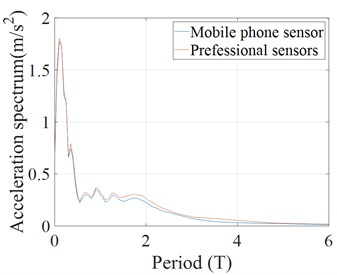
Fig. 4Power spectrum
3. Test of pedestrian overpass under ambient excitation
3.1. Test plan
The pedestrian overpass and corresponding layout of test points and are shown in Figs. 5 and 6, and in Fig. 7 the test order is presented. There are two mobile phones used in the test. As shown in the Figs. 6-7, one mobile phone sensor is moved along the pedestrian overpass to capture the vibration acceleration while the other one remains stationary [9]. The acceleration data obtained is used for subsequent analysis. The main procedure of the proposed identification method is summarized in Fig. 8.
Fig. 5Tested pedestrian overpass

Fig. 6Sketch map of pedestrian overpass

Fig. 7Test points arrangement
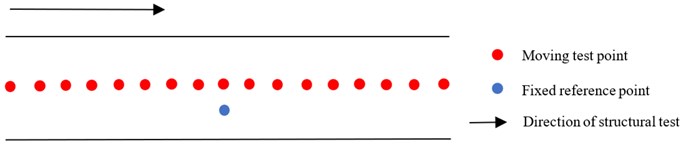
Fig. 8The procedure of the proposed identification method

3.2. Interpolation of vibration data
There are two mobile phones used in the test, and each may correspond to different sampling time, which will cause error. Therefore, the signal should be interpolated before VMD to reduce the error caused by asynchronous sampling [7]. The interpolation process is shown in Fig. 9.
Fig. 9Interpolation diagram

a) Process of interpolation (before interpolation)

b) Process of interpolation (after interpolation)
3.3. Dynamic characteristic identification
The frequency domain method is used for modal identification of the pedestrian overpass in this paper. The procedure of the identification consists two steps, i.e., (1) identification of the natural frequency, and (2) identification of the mode shapes. By analyzing the power spectrum of tested structure, the natural frequency can be determined by the frequency corresponding to the peak point of the power spectrum. In the test of pedestrian overpass, the auto and cross power spectrum density of the data can be used to identify the mode shapes of the structure. The equation for determining the mode shape can be expressed as follows:
where and are the mode coefficients of the th mode shape at the test point of and respectively; is the natural frequency of the th mode; is the self-power spectral density of the response signal at the test point ; is the cross-spectral density of the response signal of test point and test point .
In this paper, the average periodogram method is used to estimate the power spectrum density. This method divides the vibration signal data into several segments and calculates the power spectrum of each segment of data separately and then averages them. The calculation of self-power spectral density function and cross-spectral density function is shown as:
where is the Fourier transform of the th data segment of the random vibration acceleration response at a certain test point; is the conjugate complex number of ; is the data length of Fourier transform; is the average number of times [7].
4. Results and discussion
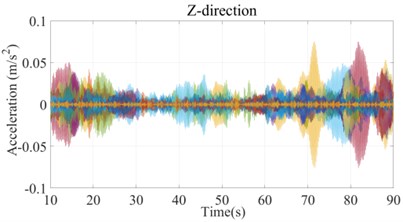
Two time histories curves of vertical vibration acceleration of the pedestrian overpass are given in Figs. 10 and 11 respectively. One is time history curve before VMD, the other is time history curve after VMD. The time history curve after VMD is smoother and the “spike” points is less, which shows that the corresponding effective components of the signal are retained and by using VMD the effects of ambient noise on vibration waveform can be effectively reduced.
Fig. 10Time history curve before VMD
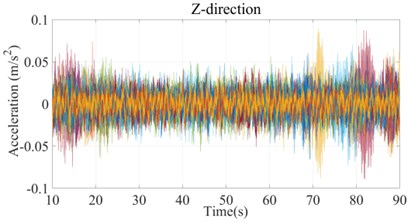
Fig. 11Time history curve after VMD
The power spectrum of corresponding to above time histories are shown in Figs. 12 and 13. There is ambient noise with frequency contents below 1 Hz in vibration data before VMD which may affect the accuracy of identification.
Fig. 12Power spectrum before VMD
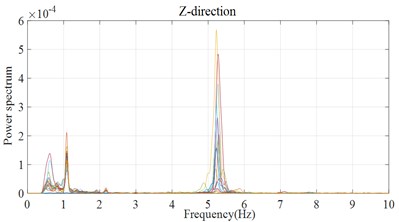
Fig. 13Power spectrum after VMD
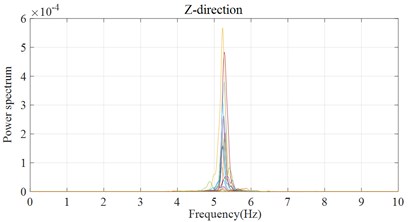
By picking the frequency corresponding to the peak point of the power spectrum, the natural frequency is identified from Fig. 13, which is about 5.22 Hz. Due to the limited minimum range of mobile phone sensor and the influence of ambient noise, only the first order mode shape (Fig. 14) can be obtained. It can be intuitively found that the identification result of the pedestrian overpass after VMD is quite consistent with the theoretical result, which proves the effectiveness of identification method. To verify the accuracy of the identification results, the numerical model of the tested structure is established for comparative analysis.
Fig. 14First order mode shape
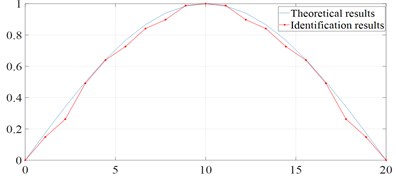
Fig. 15Simulation results of first order mode shape

The simulation result of natural frequency is 5.29 Hz, which is in good agreement with the identification result 5.22 Hz. And it can be found that the first order mode shapes of the numerical model (Fig. 15) are similar to the identification result in Fig. 14.
5. Conclusions
In this paper, mobile phone sensor replaces professional accelerometer and become the tool of structural dynamic test of pedestrian overpass, and the signal preprocessing method based on VMD is proposed to improve the accuracy of modal identification. According to the acceleration response data picked up by mobile phones, the identification results are obtained. The conclusions are as follows.
1) The accuracy and precision of mobile phone sensor meets the requirements of simple test and the structural dynamic test based on mobile phone sensor is feasible.
2) VMD is an effective way to obtain useful vibration signal which can reduce the influence of ambient noise and improve the accuracy of modal identification.
3) The structural dynamic testing based on mobile phone sensors is proved to be applicable.
To sum up, the dynamic detection based on mobile phone have the potential to be a real-time, efficient, simple, and low-cost way for structural modal identification.
References
-
Marica P., Rosario C., Rodolfo E. An automatic modal identification procedure for the permanent dynamic monitoring of the Sanctuary of Vicoforte. International Journal of Architectural Heritage, Vol. 14, Issue 4, 2020, p. 630-644.
-
Koray G., Güray G., Ahmet D. Design and realization of multi-channel wireless data acquisition system for laboratory-scale experiments on structural health monitoring. Journal of Measurements in Engineering, Vol. 6, Issue 1, 2018, p. 64-73.
-
Chalioris E., Kytinou K., Voutetaki E., et al. Flexural damage diagnosis in reinforced concrete beams using a wireless admittance monitoring system – tests and finite element analysis. Sensors, Sensors, Vol. 21, Issue 3, 2021, p. 679-679.
-
Marmolejo M. Modal Identification with Mobile Sensors Using Cohen’s Class Time-Frequency Distributions. Gaceta Técnica, Vol. 19, 2019.
-
XiaX. Comparison of Modal Analysis Methods of Environmental Excitation. Ph.D. Thesis, Central South University, 2013, (in Chinese).
-
RenW. Comparative analysis of identification methods of environmental vibration system. Journal of Fuzhou University (Natural Science Edition), Vol. 1, Issue 6, 2001, p. 80-86, (in Chinese).
-
LiZ., LinQ. Modal identification of high-rise buildings with asynchronous sampling. Journal of Natural Disasters, Vol. 05, 2009, p. 48-58, (in Chinese).
-
Zheng J. Research on Instantaneous Frequency Identification of Time-Varying Bridge Structure Based on New Signal Processing Technology. Ph.D. Thesis, Fujian Agriculture and Forestry University, 2018, (in Chinese).
-
Johannio M., Juan M., Peter T. Modal identification using mobile sensors under ambient excitation. Journal of Computing in Civil Engineering, Vol. 31, Issue 2, 2017, https://doi.org/10.1061/(ASCE)CP.1943-5487.0000619.
