Backstepping control of a tank with a flexible barrel in motion

Wang, Zong Fan; Yang, Guo Lai

doi:10.21595/vp.2020.21665

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2020

Check for updates

Backstepping control of a tank with a flexible barrel in motion

Zong Fan Wang¹

Guo Lai Yang²

^{1, 2}School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, Jiangsu, China

Corresponding Author:

Guo Lai Yang

Cite the article Download PDF

Downloads 873

Abstract

In order to simplify the dynamic equation of tank and design the controller conveniently, the barrel is often regarded as a rigid body in the previous tank barrel model. However, the barrel whose structure is a long straight pipe, is a typical flexible body in practice, it will affect the controller performance if it is directly treated as a rigid body. In this paper, we consider the flexibility of barrel and design a backstepping controller firstly. Then, Matlab and RecurDyn co-simulation were combined to compare the tracking performance of the method under different road excitation. The results show that backstepping control can adjust the muzzle angle of the flexible barrel in real-time.

Backstepping control of a tank with a flexible barrel in motion

Highlights

The research on the elastic deformation of gun barrel caused by vehicle body vibration is thorough enough.
We designed a controller using the backstepping control method for barrel flexibility.
Matlab and RecurDyn software are used for co-simulation to realize the real-time tracking of the muzzle angle of tank gun in the excitation effect of different levels of pavement.

1. Introduction

In the modern battlefield, tank weapons are required with high mobility and precision of attack, to destroy the enemy and protect themselves safely at the same time. Theory and experiment show that the perturbation of the muzzle angle of the tank barrel is the main factor which affects the firing accuracy of the projectile, so solving the problem of muzzle angle perturbation is one of the most important methods to improve the firing accuracy of a tank gun. Scholars have done a lot of research on the influencing factors of muzzle angle disturbance, which include road excitation, barrel vibration, and nonlinear fire control system, etc. [1-4]. Moreover, many achievements have been made based on the single-factor compensation research, to achieve accurate control of muzzle angle. However, considering the influence of the elastic deformation of the barrel caused by the firing of the barrel due to heat and dead weight on the muzzle angle of the barrel, the research is still not perfect. In particular, the research on the elastic deformation of gun barrel caused by vehicle body vibration is not thorough enough.

Therefore, in this paper, we established a tank dynamics model with a flexible barrel and designed a controller using the backstepping control method [5, 6] firstly. Then, Matlab and RecurDyn software are used for co-simulation to realize the real-time tracking of the muzzle angle of tank gun in the excitation effect of different levels of pavement.

2. Rigid-flexible coupling modeling for tank movement

2.1. Modeling of flexible barrel

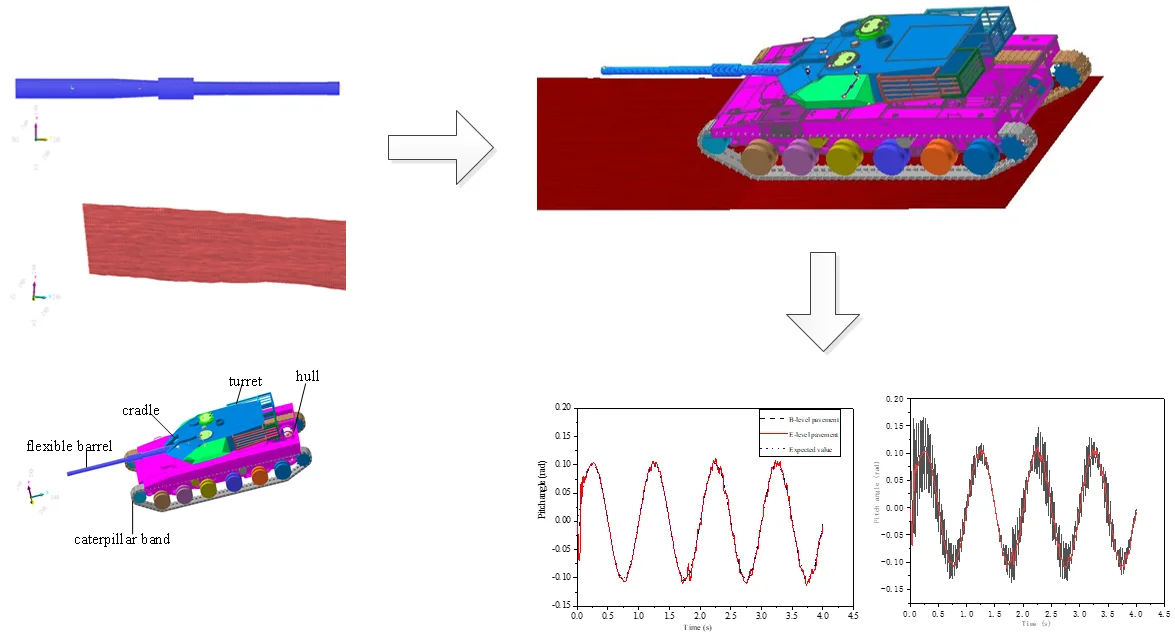
The tank barrel can be approximately treated as a long straight thick wall cylinder whose main material is steel. Therefore, it can generate elastic deformation due to the action of gravity during the driving process of the vehicle. In this paper, it is assumed that: the cross-section of the vertical gun bore axis is still flat after deformation (rigid cross-section is assumed), and the cross-section is still perpendicular to the axis after deformation. The finite element model of the body tube is drawn by using the finite element software, as shown in Fig. 1.

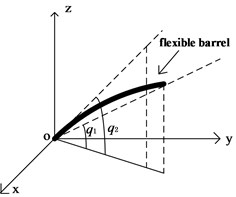
The barrel of the tank can rotate relative to the turret around the trunnion axis to adjust the vertical angle (pitch angle) of the barrel. The center of the trunnion axis is taken as the origin of coordinates, and the coordinate system is established as shown in Fig. 2. Since the horizontal disturbance of the tank is not considered in this paper, the coordinate system can be fixed on the geodetic coordinate system.

Fig. 1Finite element model of flexible barrel

Fig. 2Flexible barrel coordinate system

The dynamic equation is constructed as:

1

\{\begin{array}{l} I {\ddot{q}}_{1} + M g L s i n q_{1} + K (q_{1} - q_{2}) = 0, \\ J {\ddot{q}}_{2} + K (q_{2} - q_{1}) = u - Δ T, \end{array}

where $q_{1} \in R^{n}$ is the angle between the center of the muzzle and the ground, that is, the angle at which the projectile leaves the muzzle, $q_{2} \in R^{n}$ is the tail angle of the barrel, the default is the pitch angle of the cradle, $M$ is the mass of the barrel, $g$ is the acceleration of gravity, $K$ is the stiffness of the barrel, $I$ is the moment of inertia of the tube about the axis of the barrel, $J$ is the moment of inertia of the cradle. $u \in R^{n}$ is the control input torque, $L$ is the distance from the center of gravity of the barrel to the center of rotation, and $Δ T$ is the disturbance torque caused by road excitation.

2.2. Modeling of road uncertainty

Road roughness refers to the function of the change in road length caused by the road surface relative to the base height when the road surface is uneven. Since road roughness cannot be described by an explicit function, mathematical characteristic variance and power spectral density function are usually used to describe the road roughness. According to GB7031-2005 mechanical vibration-pavement spectrum measurement data report [9], the pavement power spectral density can be expressed as:

2

G_{q} (n) = G_{q} (n_{0}) {(\frac{n}{n_{0}})}^{- ω}, n_{d} \leq n \leq n_{u},

where $n$ is the spatial probability density, $n_{0}$ is the reference space probability density, $G_{q} (n)$ is the road roughness coefficient, $ω$ is the frequency index, $n_{d}$ and $n_{u}$ are the upper and lower spatial frequencies of the pavement spectrum, respectively. According to GB7031-2005, the road roughness can be divided into eight levels, the spatial frequency range is 0.001 m^-1 $< n <$ 2.83 m^-1, and $n_{0} =$ 0.1 m^-1, $ω =$ 2. In addition, the standard deviation of road roughness $σ_{q}$ can be expressed as:

3

\begin{array}{l} σ_{q}^{2} = \int_{0}^{\infty} G_{q} (n) d n = \int_{n_{d}}^{n_{u}} G_{q} (n_{0}) {(\frac{n}{n_{0}})}^{- 2}, \\ d n = G_{q} (n_{0}) n_{0}^{2} (\frac{1}{n_{d}} - \frac{1}{n_{u}}) . \end{array}

The road modeling method used in this paper is the white noise filtering method, which changes the road roughness coefficient according to different road levels, and uses Matlab program to simulate the road time domain model.

Fig. 3B -level road roughness

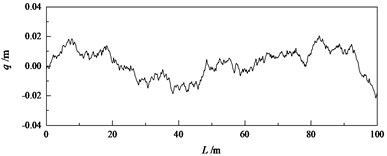
Fig. 4Modeling of B - level road

2.3. Modeling of multi-body tank

The multi-body simplified model of tank with flexible barrel is shown in Fig. 5, which is mainly composed of a caterpillar band, cradle, turret, hull and flexible barrel.

Fig. 5The multi-body simplified model of tank

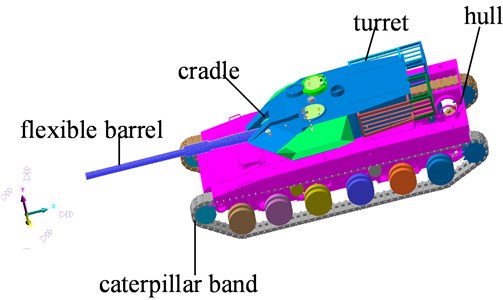
The hull and caterpillar band are connected by a suspension system, etc. The turret can rotate through the saddle ring in the horizontal plane relative to the hull, and realize the adjustment of the barrel's horizontal attitude angle. The flexible barrel can move forward and backward relative to the cradle, and simulate the counter-recoil and recoil process of the barrel during firing. The cradle can rotate vertically around the turret to adjust the pitch angle of the barrel. The influence of ground roughness has been transmitted to the hull through the caterpillar band and suspension system, which is further accurately transmitted to the flexible barrel. In this paper, we only consider the influence of the flexible barrel on the pitch angle. Therefore, the hull, cradle and turret are regarded as rigid bodies. The researches show that only gravity is taken into account, the flexibility of other parts has little influence on the angle of the muzzle when the tank is running, except the flexible barrel.

3. Design of backstepping controller

Backstepping control is a kind of nonlinear system design method in which the complex nonlinear system is decomposed into several simpler low-order systems by introducing a virtual controller. Then the Lyapunov function is selected to ensure the stability of the system, and the control law is derived. The effective control and global adjustment of the system are realized.

Define the state variable ${\dot{x}}_{1} = x_{2} = {\dot{q}}_{1}$ , ${\dot{x}}_{3} = x_{4} = {\dot{q}}_{2}$ , the Eq. (1) can be written as a state-space form:

4

\dot{x} = [\begin{array}{l} {\dot{x}}_{1} \\ {\dot{x}}_{2} \\ {\dot{x}}_{3} \\ {\dot{x}}_{4} \end{array}] = [\begin{matrix} x_{2} \\ - \frac{1}{I} (M g L s i n x_{1} + K (x_{1} - x_{3})) \\ x_{4} \\ \frac{1}{J} (u - K (x_{3} - x_{1}) - Δ T) \end{matrix}] .

First we define the expectation matrix $x_{d} = {[x_{1 d} x_{2 d} x_{3 d} x_{4 d}]}^{T}$ , and then we can get the error matrix, and the derivative of the error matrix:

5

e = [\begin{array}{l} e_{1} \\ e_{2} \\ e_{3} \\ e_{4} \end{array}] = x - x_{d} = [\begin{array}{l} x_{1} - x_{1 d} \\ x_{2} - x_{2 d} \\ x_{3} - x_{3 d} \\ x_{4} - x_{4 d} \end{array}],

6

\dot{e} = [\begin{array}{l} {\dot{e}}_{1} \\ {\dot{e}}_{2} \\ {\dot{e}}_{3} \\ {\dot{e}}_{4} \end{array}] = \dot{x} - {\dot{x}}_{d} = [\begin{array}{l} {\dot{x}}_{1} - {\dot{x}}_{1 d} \\ {\dot{x}}_{2} - {\dot{x}}_{2 d} \\ {\dot{x}}_{3} - {\dot{x}}_{3 d} \\ {\dot{x}}_{4} - {\dot{x}}_{4 d} \end{array}] .

According to Lyapunov’s stability theorem that the origin is stable if there is a continuously differentiable positive definite function $V (x)$ and $\dot{V} (x)$ is negative semidefinite. The Lyapunov function can be defined as:

7

V = [\begin{array}{l} V_{1} \\ V_{2} \\ V_{3} \\ V_{4} \end{array}] = [\begin{matrix} \frac{1}{2} {e_{1}}^{2} \\ V_{1} + \frac{1}{2} {e_{2}}^{2} \\ V_{2} + \frac{1}{2} {e_{3}}^{2} \\ V_{3} + \frac{1}{2} {e_{4}}^{2} \end{matrix}] .

It is obvious that the function $V$ is a continuously differentiable positive definite function. Its derivative can be written as:

8

\dot{V} = [\begin{array}{l} {\dot{V}}_{1} \\ {\dot{V}}_{2} \\ {\dot{V}}_{3} \\ {\dot{V}}_{4} \end{array}] = [\begin{matrix} e_{1} {\dot{e}}_{1} \\ e_{1} {\dot{e}}_{1} + e_{2} {\dot{e}}_{2} \\ e_{1} {\dot{e}}_{1} + e_{2} {\dot{e}}_{2} + e_{3} {\dot{e}}_{3} \\ e_{1} {\dot{e}}_{1} + e_{2} {\dot{e}}_{2} + e_{3} {\dot{e}}_{3} + e_{4} {\dot{e}}_{4} \end{matrix}] .

To ensure that $\dot{V}$ is negative semidefinite, the derivative of the error matrix can be expressed as:

9

[\begin{array}{l} {\dot{e}}_{1} \\ {\dot{e}}_{2} \\ {\dot{e}}_{3} \end{array}] = [\begin{matrix} - k_{1} e_{1} + e_{2} \\ - k_{2} e_{2} + \frac{K}{I} e_{3} - e_{1} \\ - k_{3} e_{3} - \frac{K}{I} e_{2} + e_{4} \end{matrix}],

where $k_{1}$ , $k_{2}$ , $k_{3}$ are positive constants, and substitute Eqs. (4) and (9) into Eq. (8), we can obtain:

10

\dot{V} = [\begin{matrix} - k_{1} {e_{1}}^{2} + e_{1} e_{2} \\ - k_{1} {e_{1}}^{2} - k_{2} {e_{2}}^{2} + \frac{K}{I} e_{2} e_{3} \\ - k_{1} {e_{1}}^{2} - k_{2} {e_{2}}^{2} - k_{3} {e_{3}}^{2} + e_{3} e_{4} \\ - k_{1} {e_{1}}^{2} - k_{2} {e_{2}}^{2} + \frac{K}{I} e_{2} e_{3} + e_{3} e_{4} + e_{4} (\frac{1}{J} (u - K (x_{3} - x_{1}) - Δ T) - {\dot{x}}_{4 d} + k_{3} {\dot{e}}_{3} + \frac{K}{I} {\dot{e}}_{2}) \end{matrix}] .

In order to make $\dot{V} \leq 0$ , we just have to satisfy ${\dot{V}}_{4} \leq 0$ . Therefore, the control input can be designed as follows:

11

u = - η s g n (e_{4}) - J (- \frac{K}{J} (x_{3} - x_{1}) - {\dot{x}}_{4 d} + k_{3} {\dot{e}}_{3} + \frac{K}{I} {\dot{e}}_{2} + e_{3} + k_{4} e_{4}) .

And substitute Eq. (11) into Eq. (10), the derivative of $V_{4}$ can be written as:

12

\begin{array}{l} {\dot{V}}_{4} = \frac{1}{J} (- η |e_{4}| - Δ T \cdot e_{4}) - k_{1} e_{1}^{2} - k_{2} e_{2}^{2} - k_{3} e_{3}^{2} + e_{3} e_{4} + e_{4} (- e_{3} - k_{4} e_{4}) \\ \leq - k_{1} e_{1}^{2} - c_{2} e_{2}^{2} - c_{3} e_{3}^{2} - c_{4} e_{4}^{2} \leq - k V, \\ k = m i n \{\begin{array}{l} k_{1} & k_{2} & k_{3} & k_{4} \end{array}\} . \end{array}

By solving the differential equation ${\dot{V}}_{4} \leq k V$ , we get the equation as follows:

13

V (t) \leq V (0) e^{- k t} .

Therefore, the proposed controller achieves an asymptotic tracking performance, i.e., $t \to + \infty$ , $e \to 0$ .

4. Simulation experiment

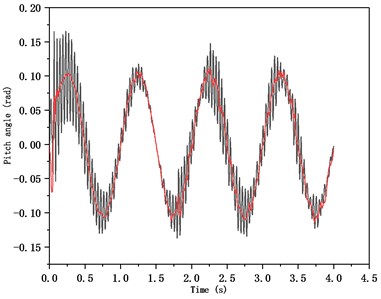
The simulation model was built in Matlab. Given initial conditions: the tank is accelerated to 30 km/s for the first two seconds and then travels at a constant speed. Add the control input of muzzle angle as $θ = 0.1 s i n (2 π t)$ , the response of tank to control on B-level and E-level pavement is analyzed as shown in Fig. 6. And compared the response of muzzle disturbance on the E-level without backstepping control as shown in Fig. 7. The results show that the muzzle disturbance can be reduced by more than 90 % under the backstepping control, and the control performance of the tank barrel is improved significantly.

Fig. 6Dynamic response of different level pavement

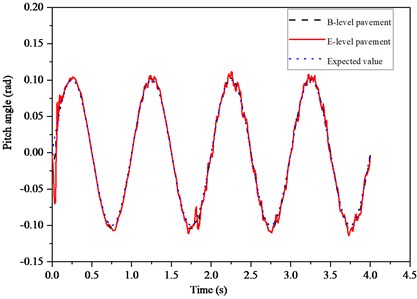
Fig. 7Dynamic response on E-level pavement compared without control

5. Conclusions

In this paper, the rigid-flexible coupling dynamics model between tanks was established based on multi-body dynamics software RecurDyn and the backstepping control method was accomplished in Matlab. This paper analyzes the tracking effect of the pitch angle of the tank barrel in driving under different levels of the road surface and verifies the feasibility of the backstepping control method in the control of flexible body pipe. In the rigid-flexible coupling model of the tank, only the barrel is regarded as a flexible body and other components as a rigid body. However, the backstepping control does not consider the thermal deformation of the body tube, and the feasibility of the controller has not been verified under the condition of continuous firing, which will be gradually improved in future work.

References

Dursun T., Büyükcivelek F., Utlu C. A review on the gun barrel vibrations and control for a main battle tank. Defence Technology, Vol. 13, Issue 5, 2017, p. 353-359.

Publisher
Zhao Z., Liu H., Chen H., et al. Kinematics-aware model predictive control for autonomous high-speed tracked vehicles under the off-road conditions. Mechanical Systems and Signal Processing, Vol. 123, Issue 15, 2019, p. 333-350.

Publisher
Chen Y., Yang G. Dynamic simulation of tank stabilizer based on adaptive control. Proceedings of the Institution of Mechanical Engineers, Part C, Mechanical Engineering Science, Vol. 233, Issue 9, 2019, p. 3038-3049.

Publisher
Deng H., Ma J., Liu H. Research on model building and simulation of self-propelled gun firing dynamics. Mechanical Science and Technology for Aerospace Engineering, Vol. 31, Issue 4, 2012, p. 543-554, (in Chinese).

Search CrossRef
Lin F. J., Shen P. H., Hsu S. P. Adaptive backstepping sliding mode control for linear induction motor drive. IEEE Proceeding Electrical Power Application, Vol. 149, Issue 3, 2002, p. 184-194.

Publisher
Swaroop D., Hedrick J. K., Pp Yip, Gerdes J. C. Dynamic surface controller for a class of nonlinear systems. IEEE Transactions on Automatic Control, Vol. 45, Issue 10, 2000, p. 1893-1899.

Publisher

About this article

Received

18 August 2020

Accepted

02 September 2020

Published

19 October 2020

SUBJECTS

Vibration generation and control

DOI

https://doi.org/10.21595/vp.2020.21665

Keywords

backstepping control

barrel flexibility

muzzle angle

co-simulation

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 03 31

Analysis of projectile-barrel coupling vibration characteristics considering the radial effect of propellant gas pressure

Cong Li, Guolai Yang, Qingbo Yu, Quanzhao Sun

Research article

2019 03 31

Launching dynamic analysis for tank on the move based on dynamic simulation

Yu Chen, Guolai Yang, Quanzhao Sun

Research article

2017 10 21

Study on measuring method of the angular displacement of muzzle vibration for the small caliber gun

Baoyuan Wang, Chunmao Ma, Diao Yang, Hongxiao Chao, Pengfei Zhang

Research article

2016 06 30

Launching dynamic analysis for truck mounted howitzer by using flexible multi-body techniques

Rateb Ragaee, Guolai Yang, Jianli Ge

Z. F. Wang and G. L. Yang, “Backstepping control of a tank with a flexible barrel in motion,” Vibroengineering PROCEDIA, Vol. 33, pp. 22–27, Oct. 2020, https://doi.org/10.21595/vp.2020.21665

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2020.21665
UR  - https://doi.org/10.21595/vp.2020.21665
TI  - Backstepping control of a tank with a flexible barrel in motion
T2  - Vibroengineering PROCEDIA
AU  - Yang, Guo Lai
AU  - Wang, Zong Fan
PY  - 2020
DA  - 2020/10/19
PB  - JVE International Ltd.
SP  - 22-27
VL  - 33
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Yang_2020,
	doi = {10.21595/vp.2020.21665},
	url = {https://doi.org/10.21595/vp.2020.21665},
	year = 2020,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {33},
	pages = {22--27},
	author = {Guo Lai Yang and Zong Fan Wang},
	title = {Backstepping control of a tank with a flexible barrel in motion},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]G. L. Yang and Z. F. Wang, “Backstepping control of a tank with a flexible barrel in motion,” Vibroengineering PROCEDIA, vol. 33, pp. 22–27, Oct. 2020, doi: 10.21595/vp.2020.21665.

Copy IEEE

Copied to clipboard!

Yang, Guo Lai, and Zong Fan Wang. “Backstepping Control of a Tank with a Flexible Barrel in Motion.” Vibroengineering PROCEDIA 33 (October 19, 2020): 22–27. https://doi.org/10.21595/vp.2020.21665.

Copy Chicago

Copied to clipboard!

Backstepping control of a tank with a flexible barrel in motion

Abstract

Highlights

1. Introduction

2. Rigid-flexible coupling modeling for tank movement

2.1. Modeling of flexible barrel

2.2. Modeling of road uncertainty

2.3. Modeling of multi-body tank

3. Design of backstepping controller

4. Simulation experiment

5. Conclusions

References

About this article

Related Articles