Abstract
Considering multiple nonlinear parameters, a nonlinear dynamic model of star gear-rotor-bearing transmission system of GTF (Geared Turbofan Engine) gearbox is established. The dynamic responses are obtained through Runge-Kutta numerical integration method, and the responses with the variation of input rotational speed are analyzed and illustrated. The abundant nonlinear characteristics are presented in the results, which could be guidance to avoid undesirable nonlinear motion, and provide a reference for the design and control of the transmission system in GTF gearbox.
Highlights
- The coupled bending-torsional nonlinear dynamic model of GTF gearbox is established.
- The multiple nonlinear parameters, including gear backlash and bearing clearance are fully considered.
- The nonlinear response of the system under varying input rotational speed are obtained.
1. Introduction
As the widely application of gearbox in wind turbine and aero industry, the nonlinear analysis for the gearbox, especially for those composed of planetary gears were studied. Zhou et al. [1] built dynamic model of the spur gear-rotor-bearing system with multiple nonlinear parameters, with the coupled lateral-torsional vibration considered. Tao et al. [2] developed a nonlinear model of a planetary gear system with multiple backlashes. Guo et al. [3] studied the nonlinear behavior of wedge teeth related to the bearing force of planetary gear system, and conducted the dynamic analysis of planetary gears considering bearing clearances [4], then studied the maximum load of planetary gears in the wind turbine drive system [5], and studies nonlinear behavior of planetary gear system in wind turbine under gravitational effects [6]. Kim et al. [7] proposed a new dynamics model for a gear set, which takes into account the torsional motion with time-varying meshing parameters. Bahk and Parker [8] conducted a dynamic analysis of the planetary gears, the resulting nonlinear behavior showed jumping phenomenon and subharmonic vibration at resonance. Li et al. [9] analyzed the nonlinear phenomena of the multi-stage planetary gear system. Zhao and Ji [10] proposed a nonlinear torsional model of gearbox in wind turbine multi-stage of planetary gear. Xiang et al. [11, 12] studied the nonlinear dynamics of multi-stage gears, which considered the multi-clearance of the system. Hou et al. [13] established a pure rotational model of the planetary gear-rotor system of the geared turbofan engine, and conducted a nonlinear dynamic analysis to obtain the torsional vibration response between the gear and the rotor. Wang et al. [14] proposed a dynamic model of GTF gearbox with elastic support of planet carrier, then [15] established nonlinear torsional model of GTF transmission system, and obtained nonlinear characteristics under excitation of important parameters.
In this paper, a coupled lateral-torsional nonlinear dynamic model of GTF gearbox is proposed, the influence of input rotational speed on the vibration response of the system is explored and quantified, then the nonlinear behavior is studied by analyzing the states of motion, mechanisms of bifurcation, and roads to chaos.
2. Dynamic model of GTF gearbox
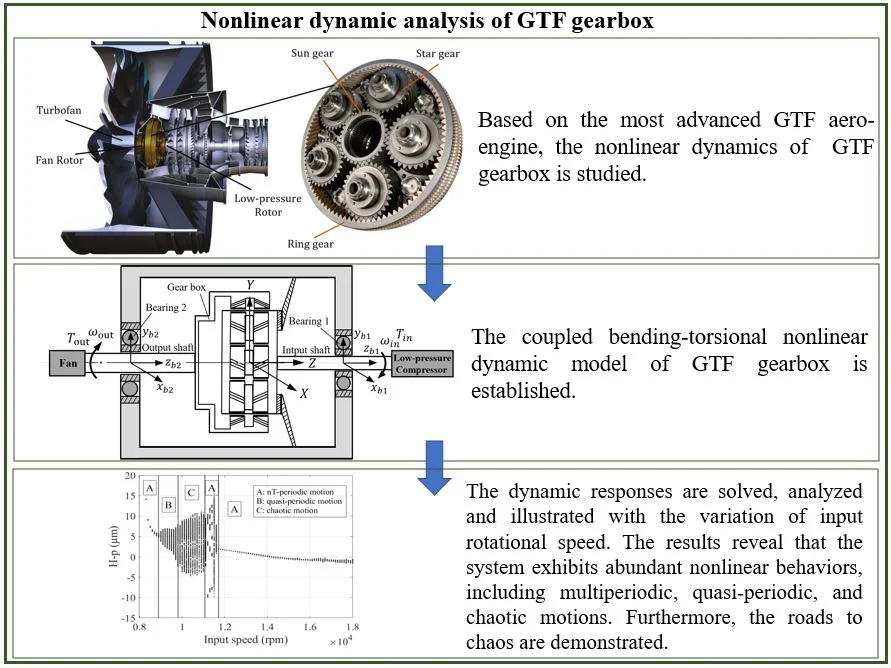
Fig. 1(a) and (b) show the physical structure and schematic diagram of star gear-rotor-bearing transmission system of GTF gearbox, which is composed of star gearing system, input shaft (the rotor between low-pressure compressor and sun gear), output shaft (the rotor that connects ring gear and fan), and bearings that support input and output rotor. The star gearing system is composed of sun gear, star gear, ring gear, and planet carrier, among which, the star gears are supported by bearings, and meshed with sun gear and ring gear, both of which are semi-floating components that splined with input and output shaft, respectively.
Fig. 1Structure of GTF gearbox

a) Physical model
b) Schematic diagram
2.1. Dynamic model of star gearing system
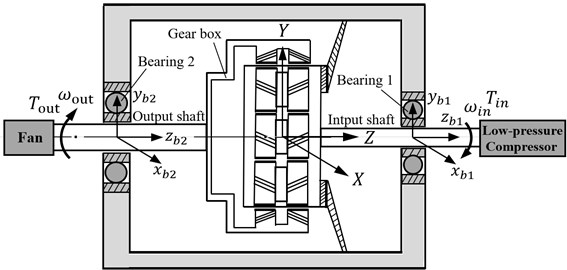
The globe coordinate system is established, base on the fixed-axis rotation of the gear components in the system. Fig. 2(a) and (b) show the model of the system, respectively. Three DOFs were considered for each components, including translational displacements and torsional displacements. The main gear components in the star gearing system were represented by the subscripts , , .
Fig. 2Modelling of star gearing system in GTF gearbox

a) Physical model
b) Dynamic model
In which, , , , indicate the meshing stiffness, and damping of external and internal meshing pairs, the value of stiffness are calculated by the formulas [16]. Then the meshing forces can be calculated by the following equations:
where , is the nonlinear function of backlash.
2.2. Mathematical model of GTF gearbox
The system has a total of DOFs, where is the number of star gears, then the overall arrays of displacement can be expressed as:
The dynamic equations of the transmission system in GTF gearbox can be derived as follows:
where is the equivalent mass in rotational direction, is the mass of components, is rotational displacement around direction, and are translational displacement in and direction. represents the input or output torque, represents torsional damping or support stiffness, represents torsional stiffness or support stiffness.
In order to eliminate the rigid body displacement, the following dimensionless variables are introduced for rotational displacement of each member. The dimensionless time parameter can be expressed by:
where, is the moment of inertia, is the radius of base circle.
Then the derived dimensionless parameters can be defined as:
where, is the dimensionless parameter of displacement.
3. Results and discussion
The basic parameters used for calculation of the nonlinear vibration response of the GTF transmission system are shown in Table 1.
Table 1Parameters of the GTF transmission system
Parameters | Value | Unit | ||
Sun gear | Star gear | Ring gear | ||
Number of teeth | 43 | 42 | 127 | – |
Helical tooth width | 60 | mm | ||
Normal modulus | 3.5 | mm | ||
Normal pressure angle | 22.5 | degree | ||
Helical angle | 27 | degree | ||
Damping ratio of meshing stiffness | 0.02 | – | ||
Comprehensive meshing error | 15 | μm | ||
Half gear backlash | 10 | μm | ||
– | Star bearing | – | ||
Bearing stiffness | 1.3e8 | N/m | ||
Bearing damping | 1.2e4 | Ns/m | ||
Bearing clearance | 5 | μm | ||
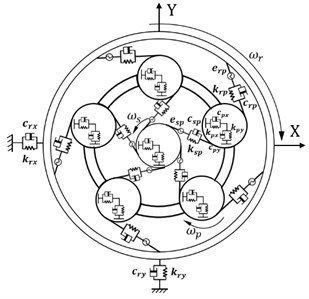
The vibration response of the system were conducted as the variation of input rotational speed, while other parameters are being constant. The bifurcation diagram of lateral displacement of star gear is shown in Fig. 3. Here, the input rotational speed (r/min) is control parameter, which varied between [8000, 18000]. As the input rotational speed increases, the system experiences periodic motion, quasi-periodic motion, and chaotic motion, successively, finally the system turns back to periodic motion through inverse bifurcation by period-doubling scenario. The nT-periodic motion is illustrated when 9000, for lateral displacement of star gear, as the input rotational speed increases from 9000 to 10000, the peiodic motion is turned into quasi-periodic motion, while the speed further increases, the chaotic motion is indicated in the system through quasi-periodicity until the speed arrives at 11500 rpm. As the further increasing of input rotational speed, the system turns back to nT-periodic motion while the input rotational speed varying from 11500 to 11900, finally the system performs periodic motion as 11900.
The vibration response of the gear system in the lateral displacement of star gear were analyzed at three input rotational speeds of 81000, 9300, and 10800, the results are shown in Fig. 4, from which different dynamic characteristics in various speed can be observed. When the control parameter 8100, the system response is dominated by the meshing frequency , the amplitude of which is much bigger than the response of other orders of meshing frequency, besides the meshing frequencies, the variable bearing stiffness frequency appears. The Poincare map that obtained shows a cluster of concentrated points when 8100, while several coincident circles are illustrated in the corresponding phase diagram, therefore, the nT-periodic motion is indicated for the system. As the control parameter 9300, although meshing frequency is still the dominant response, the multiplication frequency components of variable bearing stiffness frequencies as , , , can be observed. The Poincare map turns to be a phase-locked loop, and a trajectory torus is presented in phase diagram. The characteristic demonstrate that the gear system turned into quasi-periodic motion. As the control parameter arrives at 10800, a disordered set is shown in the Poincare map, and the corresponding phase diagram becomes a chaotic attractor with a random crew, thus, the chaotic motion is indicated for the system. In this situation, the meshing frequency is no longer the dominant response, which is replaced by the bearing stiffness frequencies and , then the multiplication of bearing frequency components , also appears with more obvious amplitudes.
Fig. 3Bifurcation diagram of system with varying input rotational speed
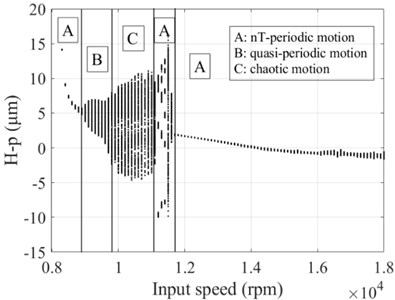
Fig. 4Vibration response of sun gear and star gear meshing pair: a) n= 8100, b) n= 9300, c) n= 10800
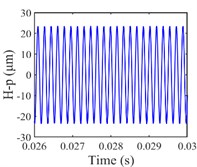
a1) Time history
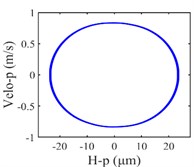
a2) Phase plane
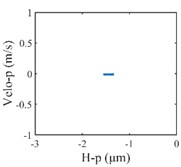
a3) Poincaré map
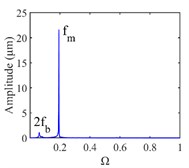
a4) FFT spectrum
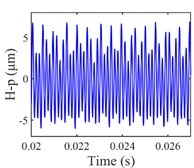
b1) Time history
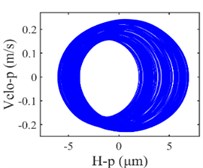
b2) Phase plane
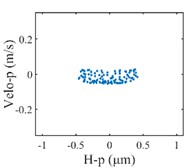
b3) Poincaré map
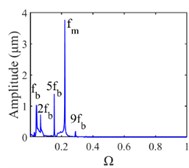
b4) FFT spectrum
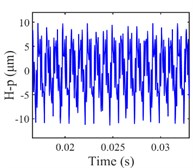
c1) Time history
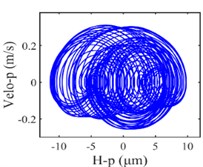
c2) Phase plane
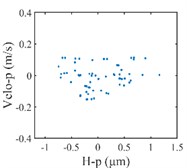
c3) Poincaré map
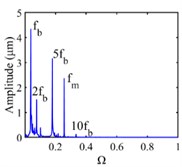
c4) FFT spectrum
4. Conclusions
In this paper, the dynamic model of the transmission system in GTF gearbox is established, based on which the coupled bending-torsional nonlinear dynamic analysis was conducted, then the influences of input rotational speed on the nonlinear dynamic response were studied. As the input rotational speed increases, nT-periodic motion, quasi-periodic motion and chaotic motion are indicated successively, however, the system finally turns into nT-periodic motion through inverse bifurcation. The nonlinear dynamic characteristics such as appearance of combination frequency components and continuous frequency components due to the increase of input rotational speed, therefore, the system should be well controlled under certain range of input rotational speed in order to avoid the chaotic motion.
References
-
Zhou Shihua, et al. Nonlinear dynamic response analysis on gear-rotor-bearing transmission system. Journal of Vibration and Control, Vol. 24, Issue 9, 2018, p. 1632-1651.
-
Tao S., Yan H. Nonlinear dynamics of a planetary gear system with multiple clearances. Mechanism and Machine Theory, Vol. 38, 2003, p. 1371-1390.
-
Yi Guo, ParkerRobert G. Dynamic modeling and analysis of a spur planetary gear involving tooth wedging and bearing clearance nonlinearity. European Journal of Mechanics-A/Solids, Vol. 29, Issue 6, 2010, p. 1022-1033.
-
Guo Y., Parker R. G. Dynamic analysis of planetary gears with bearing clearance. Journal of Computational and Nonlinear Dynamic, Vol. 7, Issue 4, 2012, p. 041002.
-
Guo Y., Keller J., Cava La W. Combine effects of gravity, bending moment, bearing clearance, and input torque on wind turbine planetary gear load sharing. American Gear Manufacturers Association Fall Technical Meeting, Dearborn, Michigan, 2012.
-
Guo Y., Jonathan K., Parker R. G. Nonlinear dynamics and stability of wind turbine planetary gear sets under gravity effects. European Journal of Mechanics A/Solids, Vol. 47, 2014, p. 45-57.
-
Kim Woohyung, Hong Hee Yoo, Jintai Chung Dynamic analysis for a pair of spur gears with translational motion due to bearing deformation. Journal of Sound and Vibration, Vol. 329, Issue 21, 2010, p. 4409-4421.
-
Bahk Cheon-Jae, Parker Robert G. Analytical solution for the nonlinear dynamics of planetary gears. Journal of Computational and Nonlinear Dynamics, Vol. 6, Issue 2, 2011, p. 021007.
-
Li S., Wu Q. M., Zhang Z. Q. Bifurcation and chaos analysis of multistage planetary gear train. Nonlinear Dynamics, Vol. 75, 2014, p. 217-233.
-
Zhao M. M., Ji J. C. Nonlinear torsional vibrations of a wind turbine gearbox. Applied Mathematical Modelling, Vol. 39, 2015, p. 4928-4950.
-
Ling Xiang, Gao Nan, HuAijun Dynamic analysis of a planetary gear system with multiple nonlinear parameters. Journal of Computational and Applied Mathematics, Vol. 327, 2018, p. 325-340.
-
Xiang Ling, et al. Nonlinear dynamics of a multistage gear transmission system with multi-clearance. International Journal of Bifurcation and Chaos, Vol. 28, Issue 3, 2018, p. 18500340.
-
Hou Lanlan, Cao Shuqian Nonlinear dynamic analysis on planetary gears-rotor system in geared turbofan engines. International Journal of Bifurcation and Chaos, Vol. 29, Issue 6, 2019, p. 1950076.
-
Wang Siyu, Zhu Rupeng Study on load sharing behavior of coupling gear-rotor-bearing system of GTF aero-engine based on multi-support of rotors. Mechanism and Machine Theory, Vol. 147, 2020, p. 103764.
-
Wang Siyu, Zhu Rupeng Nonlinear torsional dynamics of star gearing transmission system of GTF gearbox. Shock and Vibration, Vol. 2020, 2020, p. 6206418.
-
Maatar M., Velex P. An analytical expression for the time-varying contact length in perfect cylindrical gears some possible applications in gear dynamics Journal of Mechanical Design, Vol. 118, Issue 12, 1996, p. 586-589.
Cited by
About this article
The authors are grateful for the financial support provided by the National Natural Science Foundation of China under No. 51775265. In addition, the authors declare that there is no conflict of interests regarding the publication of this article.
