Abstract
Persistent exposure to whole body vibrations is the fundamental cause for lower back pain and disc degeneration. With an increasing amount of population exposed to whole body vibrations, a significant number of people experience fatal spine diseases. Substantial research is carried out to reduce the risk of spinal injuries. The dynamic characteristics of the cervical, thoracic and lumbar (CTL) region are studied extensively as individual sections of the spine. Few studies have focused on the CTL spine as an assembly of the three segments. In the present work, an authentic three dimensional geometrical model of the cervical, thoracic and lumbar spine is developed in mimics considering its natural curvature and the intervertebral discs are modeled in Design modeler. The natural frequency and mode shapes of the CTL spine are extracted using free vibration modal analysis considering 4.5 kg point mass on C1 vertebra and distributed mass of 40 kg on the CTL spine in Ansys Workbench. Six natural frequencies and their corresponding vibration modes are obtained from the finite element model. The results of this study aims to provide a reliable model for further biomechanical analysis and ergonomics.
1. Introduction
Human-machine interaction in day to day life exposes people to continuous excitation of vibration either directly or indirectly. This phenomenon is prominently observed in all operators working in manufacturing industries. Continuous exposure to machines such as power hammers, hydraulic presses, etc. leads workers to experience vibrational excitation. Majority of vehicle drivers of earth movers, trucks, helicopter, and aircraft pilots experience chronic back pain due to seat vibrations. All of the above leads to catastrophic disorders on the human spine like spondylosis, spondylarthrosis, osteoporosis, etc. The vertebral column is a part of the axial skeleton made up of the cervical, thoracic and lumbar (CTL) bones. It provides structural support and balance during physical activities like standing, sitting, and gait. The human spine is one of the most extensively investigated yet challenging areas for researchers all around the world due to limitations in the accuracy of measurements and complexities involved in modelling. The insight on the natural frequency of the CTL spine remains unclear. A finite element (FE) simulation is a research method used extensively to analyse the biomechanics of the CTL spine. It is opted over experimentation as it is unethical, and results vary from person to person based on age, size and gender. Equipment for testing and cadaver bones is rather expensive and not conveniently available to carry out the experiments. The greatest challenge in Finite element approach is the creation of an accurate three-dimensional model of the human CTL spine.
Kitazaki and Griffin [1] developed a two-dimensional finite element human model considering head mass, cervical, thoracic lumbar and pelvis region. Investigated eight resonant frequencies below 10 Hz. Reported the first resonant frequency as 1.1 Hz in fore and aft direction. Concluded the resonant frequency tends to decline as subjects move from erect to relaxed posture. Guo et al. [2] generated a finite element model of human spine T-12 to pelvis segment and obtained the resonant frequencies and mode shapes. Reported the lowest resonant frequency is in extension-flexion direction, second order resonant frequency is in lateral bending and third order is in vertical direction. Kong and Goel [3] developed a finite element beam-type model from the head to S1 and modified it to develop one motion segment (L3-L4), two motion segment (L3-L5), the complete thoracolumbar spine considering the ribcage. Reported the first natural frequency of the head to S1 model in the vertical direction as 8.32 Hz. Fan and Guo [4] developed a three-dimensional nonlinear finite element model of L1-S1 segment. Investigated dynamic response of entire lumbar spine subjected to axial cyclic loading with varying frequency. Reported the axial resonant frequency of the lumbar model as 7.77 Hz. Guo and Teo [8] generated a finite element model of human spine from lower thoracic T-12 to pelvis. The mode shape of T12-pelvis indicates the human upper body primarily performs the vertical motion during whole body vibration and the lumbar spine section translates and rotates in the sagittal plane. Flexion is observed in the lower segments and extension in the upper segments of lumbar spine.
Modal analyses on cervical, thoracic or lumbar vertebrae as an independent system is reported as a dedicated research work whereas the CTL spine as a whole has not been considered. In the present work, a three-dimensional model is developed by reconstructing the geometry obtained from computed tomography (CT) scans. An attempt is made to develop an accurate continuous FE model of the CTL spine. The dynamic characteristics of the human CTL spine as a whole are extracted. The vertebral body, intervertebral discs and spine’s natural curvature is incorporated during modal analyses. The natural frequency and mode shape of the CTL spine is determined. The findings of the present work contribute towards qualitative work in the area of whole body vibration (WBV), spine related product design and development.
2. FE modelling
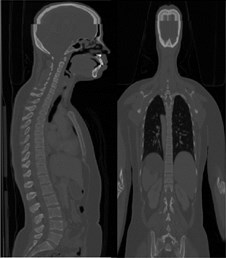
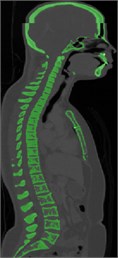
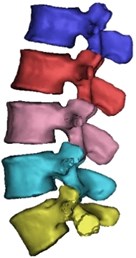
Computed tomography (CT) scan of a healthy female volunteer with history of no spine disorders is considered for the present work. A three-dimensional FE model of a CTL spine is constructed using the data extracted from the CT scan. Fig. 1(a) shows CT scan in DICOM (Digital Imaging and Communications in Medicine) format, showing front view (coronal) and side view (sagittal) of the subject. It consists of 701 slides where each slide is 2 mm thick. The DICOM images are imported into MIMICS 21.0 software and are shown in Fig. 1(b). The segmented 3D surface model is imported to 3-MATIC 21.0 for post processing. Fine tuned and segmented 3D assembled view of vertebra is shown in Fig. 1(c).
Fig. 1a) CT scan in DICOM format, b) Segmentation in MIMICS 21.0, c) Accurate surfaces in 3-Matic
a)
b)
c)
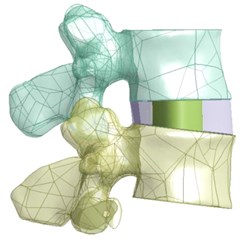
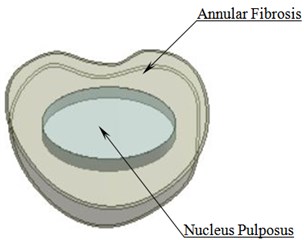
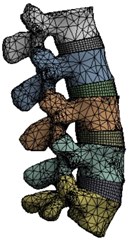
A solid 3D geometrical model developed in 3-MATIC is imported to ANSYS workbench 18.1. The soft tissues that cannot be developed during CT imaging is created and assembled in Design Modeller. Fig. 2(a) shows L3-L4 vertebrae with an intervertebral disc (IVD) in an assembled view. The IVD comprises of annular fibrosis and nucleus pulposus as shown in Fig. 2(b). Fig. 2(c) shows a meshed model of lumbar region.
Fig. 2a) L3-L4 vertebrae with IVD b) Intervertebral disc c) Meshed model of lumbar region
a)
b)
c)
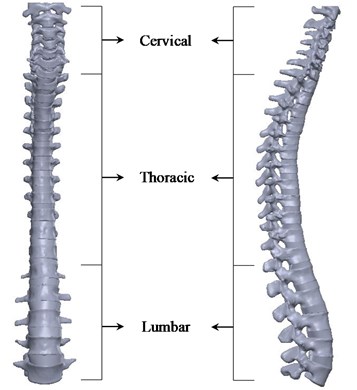
Using the same procedure, the entire CTL spine with intervertebral discs is developed. Front view and lateral view of the CTL spine is shown in Fig. 3. It consists of 7 cervical, 12 thoracic and 5 lumbar vertebral bones with 22 intervertebral discs. All the vertebrae are lined independently over each other separated by an intervertebral disc except between Atlas (C1) and Axis (C2) bones.
Fig. 3Front view (left), lateral view (right) of the CTL spine with intervertebral discs
The CTL model is meshed using adaptive size function, with each element of size 2 mm. The generated mesh comprises of 9,33,229 nodes with 5,53,187 elements. Modal analysis is performed considering the inferior surface of L5 vertebra as fixed. The facet contact is set to a surface-to-surface frictionless interaction and other surface contacts among the vertebral bones and intervertebral discs are defined as bonded interaction. A point mass of 4.5 kg is assumed to depict the head, acting on the superior surface of the C1 vertebra. The upper body mass of 40 kg is applied as distributed mass on the CTL spine [2]. The natural frequency and mode shapes of the CTL spine are extracted and discussed in the following section.
Table 1Material properties of CTL finite element model [4, 8]
Component | Density, (kg/m3) | Young’s modulus, (MPa) | Poisson’s ratio, |
Cancellous bone | 1100 | 100 | 0.2 |
Posterior bone elements | 1400 | 3500 | 0.25 |
Nucleus pulposus | 1020 | 1 | 0.49 |
Annular fibrosis | 1000 | 500 | 0.3 |
3. Results and discussions:
An accurate 3D FE model is used to determine the resonant natural frequencies and mode shape of the CTL spine. A 3-D continuous structure may have infinite natural frequencies and mode shapes. The first six mode shapes are investigated extensively since low frequency vibration mode has a major impact on the human spine. They are in fore-and-aft, lateral bending, flexion extension and torsion.
By careful observation it is noticed the frequency of the first vibration mode is 0.97 Hz, in fore-and-aft motion caused by the bending deformation of the spine as shown in Fig. 4(a). This mode of vibration is similar to the first mode of a cantilever beam. Second mode corresponds to lateral bending at a frequency of 1.26 Hz as shown in Fig. 4(b). The third mode is in flexion-extension direction at a frequency of 4.88 Hz. In the 3rd mode shape as shown in Fig. 4(c) a phase difference is observed between cervical and thoracic region. The 4th mode shape exhibits torsional motion at a frequency of 6.14 Hz as shown in Fig. 4(d). The 5th mode shape exhibits flexion extension motion at a frequency of 13.89 Hz as shown in Fig. 4(e). It is observed that maximum deformation is in the cervicothoracic region. The 6th mode occurs at a frequency of 16.36 Hz and exhibits torsional motion. The amplitude of vibration of T12-L2 is observed to be larger than those of other segments.
Fig. 4a) First mode shape, b) second mode shape, c) third mode shape, d) fourth mode shape, e) fifth mode shape, f) sixth mode shape

a) Mode 1, 0.97 Hz, fore and aft

b) Mode 2, 1.26 Hz, lateral bending

c) Mode 3, 4.88 Hz, flexion extension

d) Mode 4, 6.14 Hz, torsion

e) Mode 5, 13.89 Hz, flexion extension

f) Mode 6, 16.36 Hz, torsion
4. Conclusions
A detailed 3D FE model considering the curvature of the human CTL spine is developed from CT scans. The CTL spine consists of 24 vertebral bones and 22 intervertebral discs. The head is assumed to be a point mass of 4.5kg acting on C1 vertebra and upper body mass of 40 kg is applied as a distributed mass on the CTL spine. Modal analysis is performed to obtain the dynamic characteristics. Six natural frequencies and the corresponding mode shapes-fore and aft, lateral bending, flexion extension and torsion are investigated. It is observed that the predominant mode of vibration occurs in vertical direction. The cervical region of the CTL model undergoes larger deformations when compared to the thoracic and lumbar regions. Few limitations of this model include the lack of ligaments, end plates and annular matrix in the intervertebral discs. This model can be further used to estimate the dynamic response, stress and strain analysis for various applications.
References
-
Kitazaki S., Griffin M. J. A modal analysis of whole-body vertical vibration, using a finite element model of the human body. Journal of Sound and Vibration, Vol. 200, Issue 1, 1997, p. 83-103.
-
Guo Li Xin, Zhang Yi Min, Zhang Ming Finite element modelling and modal analysis of the human spine vibration configuration. IEEE Transactions on Biomedical Engineering, Vol. 58, Issue 10, 2011, p. 2987-2990.
-
Kong Wayne Z., Goel Vijay K. Ability of the finite element models to predict response of the human spine to sinusoidal vertical vibration. SPINE, Vol. 28, Issue 17, 2003, p. 1961-1967.
-
Wei Fan, Li Xinguo Influence of different frequencies of axial cyclic loading on time-domain vibration response of the lumbar spine: a finite element study. Computers in Biology and Medicine, Vol. 86, 2017, p. 75-81.
-
Pal G. P., Routal R. V., Saggu S. K. The orientation of the articular facets of the zygapophyseal joints at the cervical and upper thoracic region. Journal of Anatomy, Vol. 198, 2001, p. 431-441.
-
Iris Busscher, Ploegmakers Joris J. W., Verkerke Gijsbertus J., Veldhuizen Albert G. Comparative anatomical dimensions of the complete human and porcine spine. European Spine Journal, Vol. 19, 2010, p. 1104-1114.
-
Zhou S. H., Mccarthy I. D., McGregor A. H., Coombs R. R. H., Hughes S. P. F. Geometrical dimensions of the lower lumbar vertebrae – analysis of data from digitised CT images. European Spine Journal, Vol. 9, 2000, p. 242-248.
-
Guo L. X., Teo E. C. Prediction of the modal characteristics of the human spine at resonant frequency using finite element models. Proceedings of the Institution of Mechanical Engineers, Part H, Vol. 219, Issue 4, 2005, p. 277-284.
-
Dupuis H., Zerlett G. The Effects of Whole body Vibration. Springer-Verlag Berlin Heidelberg, 1986.
