Abstract
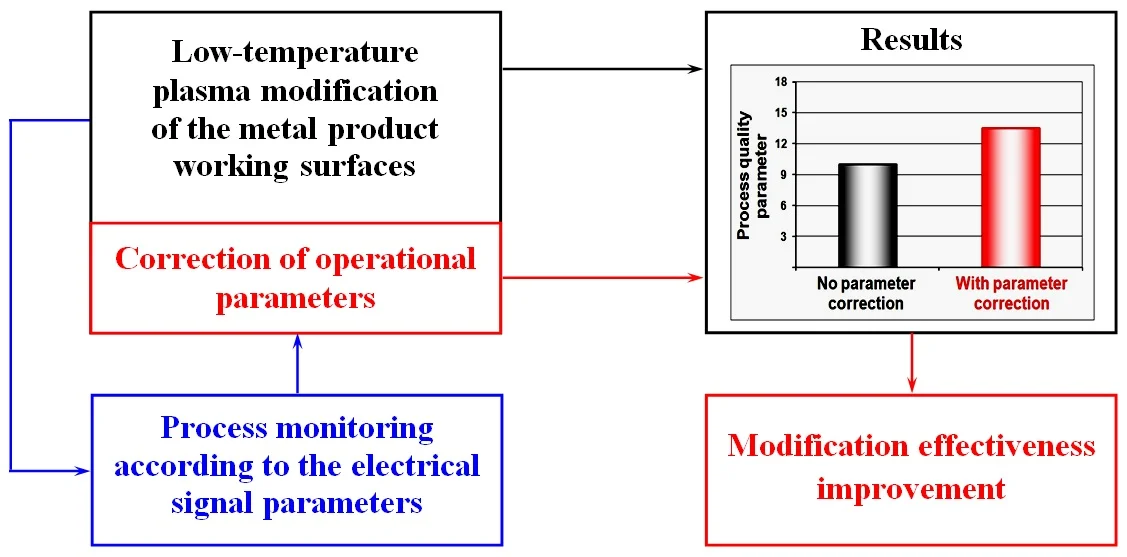
The paper shows good prospects of modifying the working surfaces of metal products by low-temperature plasma treatment. We suggest a treatment monitoring method based on the recording of signals that arise in the electrical circuit of the processing unit and present the results of this approach realization. The study substantiates the expediency, assesses possibility, and shows the efficiency of controlling the low-temperature plasma modification based on the correction of its operating parameters according to monitoring data.
Highlights
- Modification of the working surfaces of metal products by means of low-temperature plasma contributes to the formation of their unique strength and corrosion properties.
- The efficiency of the modification process is increased by implementing its monitoring according to the electrical signal parameters.
- Correction of the operational parameter values according to monitoring data ensures the modification process stabilization and makes it possible to control its progress.
- When solving the control problem, it is not the control signal power that is important but its semantic content.
1. Introduction
Modification of the working surfaces of metal products for various purposes is one of the promising research directions for increasing their reliability in terms of durability. There are various modification methods (heat treatment, coating, treatment with concentrated electron and photon fluxes, treatment with concentrated ion beams, plasma treatment) that allow modifying the properties of the surface layer to varying degrees and contributing to its hardness increase to varying degrees.
It is known [1] that the best results correspond to a situation in which the modification provides nanostructuring of the surface layer; then its hardness achieves a maximum value. However, the listed methods do not ensure the surface layer nanostructuring, since their main mechanisms of changing its properties are diffusion incorporation and alloying. Besides, the methods have high energy consumption and product exposure time that can lead to a change in their dimensional and geometric parameters, and with their help it is impossible to modify the working surfaces of complex and precision products.
One of the directions of modification is the exposure of the product surface to a low-temperature plasma of a combined discharge according to the method developed by the authors of the article. The exposure is performed in a processing unit (Fig. 1(a)) built for the method implementation and is based on the formation of a plasma cloud directly around the product when electrostatic and microwave electromagnetic fields are applied to it in a process gas medium at a pressure of 300 Pa [2]. An electrostatic field forms a stream of charged plasma particles generated during the ionization of atoms and molecules in a gas due to the electromagnetic field, to the product surface. This contributes to the release of the amount of heat sufficient for melting a thin surface layer, and leads to significant structural and phase changes. As a result, a composite structure is formed in the surface layer, consisting of 30-200 nm particles (nanoclusters) and particles < 10 nm (amorphous bond between clusters), which gives the surface layer unique properties that provide [3]:
– 1.4-2.9-fold improvement of roughness;
– increased wear resistance, 2.35-3.13-fold on average, with a maximum of up to 5.0-fold increase;
– strength improvement by microhardness parameter: 1.5-fold average increase; 2-fold maximum increase;
– 1.5-2.9-fold increase in corrosion resistance in a neutral solution; in acidic solution: 6.0-fold average increase, up to 12-fold maximum.
Modification time is no more than 10-15 minutes, the parameters of the initial dimensional and geometric product accuracy remain unchanged. In this case, most of the energy is spent on the process, unlike other plasma methods where most of the energy is spent on creating plasma, maintaining the its generation conditions and delivery of active particles with energy to the product, followed by scanning them on the surface.
The studies performed showed that the effectiveness of modification depends on how much its operating parameters – the magnetron anode current () and displacement potential () – retain their efficiency under the changing properties of the product surface layer. In this regard, studies have been carried out on the rationale for monitoring the process according to the parameters of the signals arising in the electrical circuit of the processing unit [4-6]. The research results served as the basis for solving the problem of monitoring and evaluating the possibility of controlling the process of low temperature plasma modification in order to increase its efficiency.
Fig. 1a) Processing unit and b) elements of the feedback channel implemented in it according to the electric signal parameters: 1 – resistor sensor, 2 – analog-to-digital converter

a)

b)
2. Approaches and results
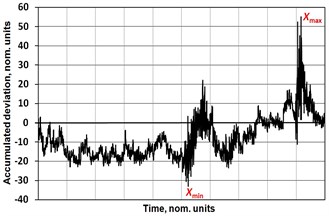
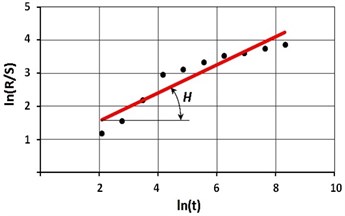
The problem was solved in three stages. At the first stage, a feedback channel was formed (Fig. 1(b)), which enabled recording and transmitting electrical signals to the processing unit control system (Fig. 1(a)). For the quantitative assessment of the processed signals, the Hurst statistics () [5, 7] was used, which is the slope angle of the log regression line of the averaged values of signal swings () normalized to the standard deviation (), as the differences between the maximum () and the minimum () deviations of the signal from the average value (Fig. 2(a)) accumulated over a fixed time interval t, and which reflects the effect of each averaged indicator (i.e. actually the structure of the signal) on the direction and the degree of its change (Fig. 2(b)). The reliability of Hurst statistics calculation depends on the length of the electrical signal and its sampling frequency.
At the second stage, a monitoring algorithm and its software were developed using the Microsoft .NET Framework version 4.5. Data is obtained using RSH Software Development Kit version 2.1.
The algorithm consists of the following steps:
1) data input for monitoring: the duration in the number of points of recording an electrical signal with frequency ; signal recording frequency ; the product processing time at the given values of and ; number of points , starting from which the significance of the trend change of Hurst statistics is assessed; table value of Student -criterion ; parameter used to form arrays of obtained values ;
2) signal registration during product processing;
3) statistics calculation; formation of an array of calculated values;
4) if the volume of the array is greater than or equal to , then the construction of the linear regression equation and the estimation of its angular coefficient significance using Student’s criterion [4], otherwise, the transition to checking the condition for the end of processing time;
5) if the angular coefficient is insignificant, then checking the condition for the end of processing time;
6) if the angular coefficient is significant, then checking its sign;
7) if the sign is positive, then notification on the need to correct the operating parameters values with the subsequent return to signal registration;
8) if the sign is negative, then the formation of a new array for storing the values of Hurst statistics and checking the condition for the end of processing time;
9) if the processing time has not ended, then the signal registration continues;
10) end of work.
Fig. 2a) Initial data and b) calculation pattern of Hurst statistics: points represent the values of normalized accumulated ranges R/S calculated according to cumulative curves a), the right line is the regression line
a)
b)
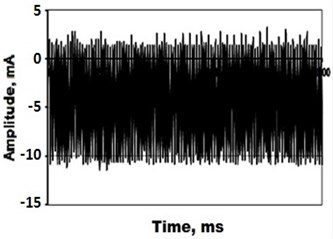
The results of the algorithm testing and analyzing electrical signals recorded on the processing unit during experiments with a RX-10 alloy sample on various combinations of and values showed (Table 1) that they do not have a characteristic scale, i.e. are fractal (Fig. 3), and characterize the behavior of the process of exposure to low-temperature plasma on the surface as chaotic, especially if is greater than 0.5. This is due to changes in the conditions of the processing under the influence of various disturbances: fluctuations in the operating parameters, pressure and temperature in the processing unit working chamber, as well as the product surface layer properties; and it led to the conclusion about the advisability of process correction.
Table 1H values of electrical signals
, mA | , V | |||
100 | 125 | 150 | 175 | |
25 | 0.424 | 0.503 | 0.351 | 0.621 |
35 | 0.424 | 0.333 | 0.589 | 0.378 |
45 | 0.766 | 0.605 | 0.672 | 0.592 |
55 | 0.849 | 0.709 | 0.69 | 0.703 |
65 | 0.776 | 0.741 | 0.825 | 0.751 |
75 | 0.78 | 0.258 | 0.812 | 0.97 |
85 | 0.229 | 0.322 | 0.923 | 0.275 |
At the third stage, the implementation of the working surface modification monitoring was carried out for a 6 mm diameter drill of P6M5 steel at a length of 15 mm. During processing, the moment of the need to correct the operational parameters values was determined (Fig. 4) using the developed algorithm (see steps 6, 7), however, since the Hurst statistics value was in the range of permissible values (0-0.5) [4, 5], the processing continued without correction. This led to the decrease of the plasma glow intensity and the cloud diameter 3.5 minutes before the end of processing, therefore, in order to maintain the plasma, the value of magnetron anode current was adjusted twice to increase its value (moments 1 and 2 in Fig. 4).
Fig. 3Electrical signal types recorded on the processing unit during experiments with an RX-10 alloy sample, for a) H< 0.5 and b) H> 0.5
a)
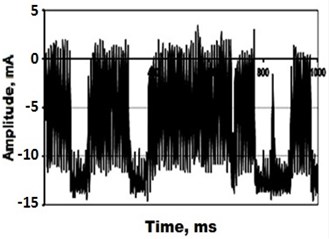
b)
Fig. 4The behavior of Hurst statistics when processing P6M5 steel drill: K is the moment of the need to correct the value of Ia determined using the developed algorithm; 1, 2 are the moments of the actual correction of Ia value
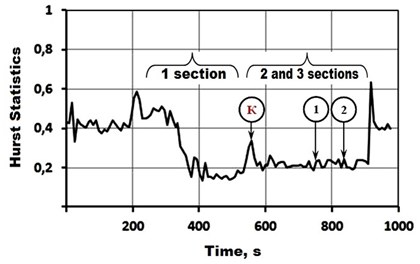
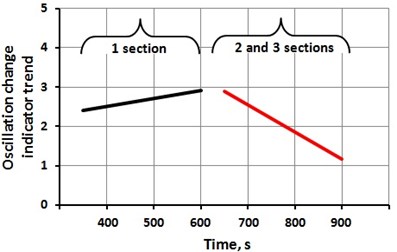
To establish the causes for such plasma behavior by methods of the automatic control theory, additional processing of the recorded electric signal was performed. It consisted in the calculation of the amplitude-phase frequency characteristics of the signal in the sections before and after value correction (1, 2 and 3 in Fig.4) as well as the calculation of its oscillation index at a frequency at which the characteristic crosses the real axis, determining the stability margin of the plasma-article system according to the module. Trend graphs of the oscillation index change before and after corrections of (Fig. 5) showed the following.
The decrease in the radiation intensity of the plasma cloud was accompanied by an increase in the oscillation index (1 section), which means a reduced stability margin of the plasma-product system and its movement to the stability boundary (in this case, the physical meaning of the stability boundary is that the plasma goes out completely). A change in (sections 2 and 3) led to a decrease in the oscillation index and the eventual stability margin restoration to a level that is considered practically necessary (1.2...1.5) (in this case, for stable plasma combustion).
The reliability of the obtained results was confirmed by comparing the microhardness increments of the surface layer of the drill processed with the magnetron anode current correction and the drill processed without correction, which showed that the correction provided an increment of 1.35 times greater than the increment obtained without correction.
Fig. 5Oscillation trends
3. Results and discussion
The performed studies allow us to conclude that in the case of chaotic behavior of the process of low-temperature plasma exposure on the surface of the product, the its organization and monitoring by electrical signals are advisable, as they enable to determine the moments of adjustment of operating parameters and make it possible to control the process. It should be noted that in technical systems the control signal is usually very small compared with the force acting through the power amplifier on the corresponding object. In particular, a two-time change in value during processing by only 10 % led to an increase in the workpiece surface microhardness by 35 %. This means that while solving low-temperature plasma modification control problems, it is not so much the signal power that matters, but its meaning. In this regard, the following should be taken into account.
In recent times more and more attention has been paid to the problem of revealing the connection between the behavior of complex nonlinear dynamic systems and the information processes arising from them as a result of interaction with the external environment. Synergetics has shown that information processes occur in systems located at the stability boundary and exhibiting the ability to go to an ordered state as a result of fluctuations [8, 9]. Owing to the influx of external energy, nonequilibrium arising due to fluctuations are not eliminated, but rather increase, accumulate and intensify due to the positive system reactivity, triggering irreversible dissipative processes that lead, on the one hand, to various consequences, especially at bifurcation points [9], and to the production of information (negentropy) on the other hand. If the information production is considered as the process of generating some signals that characterize a particular reaction of the system to the action of an external (or internal) environment, then the monitoring data can be considered as a representation of these reactions, which correspond to the path of the feedback signal (in this case, statistics ). The monitoring will be effective if the results of the feedback signal analysis allow the formation of such control signals that will not only be able to direct the trajectory in the right direction but also decrease its oscillation degree i.e. reduce fluctuations.
If we consider fluctuations as possible system microstates which are a measure of the phase space available to it, then its logarithm will determine the entropy of the system: , where is Boltzmann constant [8]. Hereof it follows that the disorder introduced into the system at the macro level is proportional to the increase in the number of its microstates: . This means that the relative decrease in the number of possible states of the system under the action of control is proportional to the decrease in its disorder, i.e. compression of the phase volume. In the limit, when one state is established in the system ( 1), its entropy vanishes and the system comes into equilibrium [9].
4. Conclusions
1. The efficiency of low-temperature plasma modification as a promising way to improve the reliability of complex and precision products can be increased by controlling the operating parameters based on the registration and processing of electrical signals.
2. For the practical implementation of the control, a complex of issues related to the technology development needs to be solved, including the determination of: a parameter advisable to adjust, time point of correction, correction method.
3. The control efficiency can be determined by the results of the Fisher criterion calculation [10], which allows to evaluate the quality of the formed trajectory of statistics change according to the reducing variance of its value estimates. For this purpose, in the stored arrays , the sample variances and are calculated to the operating parameters correction moment and from the moment of its beginning, as well as the Fisher criterion , provided that . values are compared to a table value for a given significance level . If it turns out that , this will mean low management efficiency, since the spread in estimates has decreased insignificantly. In case it turns out that this will indicate efficient management, since the spread in the estimates has decreased significantly. Moreover, the degree of management efficiency is higher, the more the condition is met in more cases and the greater the values. In particular, according to the data in Fig. 4 values of the Fisher test were 6.92 and 5.15 with tabular values at a significance level of 0.05, respectively, 2.54 and 2.93, i.e. the process control proved to be efficient.
References
-
Grigoriev S. N. Methods for Increasing the Resistance of the Cutting Tool. Machine Building, Moscow, 2009.
-
Brzhozovskii B., Brovkova M., Gestrin S., Martynov V., Zinina E. The effect of a combined low-pressure gas discharge on metal surfaces. Journal of Physics D: Applied Physics, Vol. 51, 2018, p. 145204.
-
Brzhozovsky B., Martynov V., Zinina E., Brovkova M., Bochkarev P. The synthesis of nanocomposite structures on the surface of geometrically complex products. IOP Conference Series: Materials Science and Engineering, Vol. 140, 2016, p. 012002.
-
Martynov V., Brzhozovskii B., Zinina E., Yankin I., Susskiy A. Fluctuations in the process plant as a quality assessment criterion of low-temperature plasma hardening process. Procedia Engineering, Vol. 176, 2017, p. 451-460.
-
Azikov N., Brzhozovskii B., Brovkova M., Martynov V., Zinina E., Susskii A. Improved efficiency of the process of low-temperature plasma hardening based on its monitoring. Journal of Machinery Manufacture and Reliability, Vol. 46, Issue 6, 2017, p. 582-588.
-
Brzhozovskii B., Martynov V., Susskii A. Information-measuring channel development for low-temperature plasma hardening monitoring. Automation. Modern Technology, Vol. 72, Issue 12, 2018, p. 546-549.
-
Feder E. Fractals. Mir, Moscow, 1991.
-
Kolesnikov A. A. Synergetics. Software and Systems, Vol. 1, 2002, p. 3-6.
-
Nicolis G., Prigogine I. Self-Organization in Nonequilibrium Systems. From Dissipative Structures to Order Through Fluctuations. Mir, Moscow, 1979.
-
Mitropolsky A. K. The Technique of Statistical Computing. Nauka, Moscow, 1971.
Cited by
About this article
The authors express their gratitude to the Russian Science Foundation, through a grant of which (Project No. 19-19-00101) the present study was carried out.
