Abstract
This paper is devoted to the problem of providing the required synchronous modes of oscillations of a jaw crusher with self-synchronizing inertial vibration exciters. The described mathematical model of the crusher takes into account the mechanical properties of the medium being processed and the possible asymmetry of its contact with the crusher’s working bodies – the jaws. A numerical analysis of synchronous modes of crusher vibrations with different asymmetries of the initial location of the processed medium relative to the jaws is done. It is shown that for given oscillation excitation frequencies, the non-simultaneous contact of the processed medium with the jaws can lead to a change in the types of synchronous vibrations of the jaw crusher.
1. Introduction
One of the problems of creating efficient vibratory jaw crushers with two movable jaws, which oscillations are excited by self-synchronizing inertial vibration exciters, is the provision of synchronous jaws’ antiphase oscillations [1-3]. The type of synchronization of the exciters’ rotation and the jaws’ oscillation forms have a mutual influence on each other and are determined by the mechanical parameters of the system, the processed mediums characteristics, the electric drive’s parameters of vibration exciters and their rotation frequency [3, 4]. When studying the dynamics of such crushers, it is especially difficult to take into account the interaction of the jaws with the medium being processed [2, 5, 6]. In mathematical models used in common computational practice, this interaction is usually taken into account in the form of viscous friction forces [5, 7, 8]. At the same time, factors excluded from consideration, such as non-simultaneous contact of the jaws with the processed medium, its elastic properties, as well as the vibro-impact nature of its interaction with the crusher’s jaws, can have a significant influence on the systems dynamics.
This paper is devoted to identifying the effect of non-simultaneous interaction of jaws with the processed medium, taking into account their impact contact, on the exciters’ self-synchronization and jaws’ movement.
2. Design scheme and the mathematical model of the jaw crusher
The solution of the problem is based on the analysis of the vibrating jaw crusher’s dynamics with two movable jaws that perform straight horizontal oscillations excited by two inertial vibration exciters installed on each of the jaws. The design scheme of such a crusher is shown in Fig. 1. The crusher’s body is modeled by a solid body of mass , elastically attached to a fixed base. The jaws are modeled by identical solids with mass . The jaws are attached to the crusher’s body with the identical elastic elements. It is assumed that all elastic elements have linear stiffness and damping characteristics with coefficients , and , , respectively. On each of the jaws the same unbalance vibration exciter is fixed, driven by an asynchronous motor of limited power whereas and – each vibration exciter’s imbalanced mass and eccentricity, – adduced moment of inertia of the vibration exciter’s asynchronous motor, – torque of the th vibration exciter’s electric motor ( 1, 2) described by the static characteristic [9]. The friction in the bearings of the unbalance shafts is taken into account in the form of the moments of dry friction’s forces (not shown in Fig. 1).
Between the jaws there is a processed medium modeled by a solid body with two (one on the left and one on the right) identical elastic elements, with stiffness and viscosity coefficients and , respectively, providing one-way interaction with each of the jaws. In addition, the body is attached to a fixed base by a linear elastic element with stiffness and viscosity coefficients and , respectively, which ensures that the modeled medium returns to its initial position only when there is no contact with the jaws. In this way, the inflow of a new unprocessed part of the medium through the crusher’s fixed loading window into the working space between the jaws is simulated. In the initial state, the working bodies can be installed with a gap (pre-tension) relative to the contact elements, which is given by the values and .
Displacements of the bodies are described by coordinates ( 1, 2, 3, 4) of their centers of mass, measured from their equilibrium position. The positions of the debalances are described by the angles of rotation ( 1, 2), measured from the negative direction of the axis .
Fig. 1Design scheme
The equations of the system motion in a dimensionless form are:
where:
, , , , , , , , , – dimensionless coordinates, , – given eccentricity initial value, – time scale:
where and critical torque and slip of the asynchronous motor, – denotes direction of the motors’ rotation, , – synchronous speed of rotation of the electric motor, – frequency of the supply voltage, – number of pole-pairs of the electric motor, , – coefficient of dry friction, dots indicate differentiation by dimensionless time . The presented equations system allows to analyze the crusher’s motion, taking into account the non-simultaneous impact of the jaws on the processed medium and their impact contact.
3. The results of modeling the crushers dynamics
The system oscillations were simulated numerically in Matlab using standard functions for integrating differential equations with the condition to accurately determine the time of the beginning and the end of the jaw’s contact with the processed medium.
At the first stage, the frequency ranges of synchronous exciters’ rotation and jaws’ motion were determined in the absence of the processed medium (the standard task of studying the frequency ranges of the exciters’ synchronous rotation and the crusher’s vibration modes with the aim of selecting its operating modes). For this, the frequency of the supply voltage was set, which discretely increased in the range of 0.1 ≤ ≤ 2.5 with a step 0.5 and an exposure at each step during 400 sufficient to achieve steady-state oscillations of the system (the law of change is shown in Fig. 2). In this case, in the considered frequency range , the maximum torque of the engine was considered to be a constant value. The calculations were carried out with the following system parameters: 2, 0.05, 0.03, 0.1, 1, 0.5, 1, 10, 1, 100, 0.2, 0.001, 0.61, 0.005, , .
Fig. 2Power supply frequency ωe in time τ
In Fig. 3 and Fig. 4 the results of calculating the rotational velocity of the inertial exciters and the mutual phase shift of the rotation between the exciters as a function of time are shown, respectively. The value of 180° corresponds to the synchronous antiphase rotation of the exciter’s debalances, which causes the antiphase oscillations of its jaws required for the crusher’s normal operation. When 0°, the debalances rotate in phase, exciting the common-mode oscillations of the crusher’s jaws. One can see from Fig. 2 and Fig. 4 that the required synchronous modes of the debalances rotation and, accordingly, oscillations of the crusher are realized in the ranges of supply voltage frequencies [0.8, 1.2] and [1.85, 2.5]. Fig. 2 and Fig. 3 show the relationship between the power supply frequency and the rotational velocities of the debalances. It also can be seen that in the indicated ranges of the supply voltage frequency, the debalances rotate with the same angular velocity in absolute value. When approaching the second and third resonant frequencies ( 0.976, 1.445), the rate of change of an average rotational velocity of the debalances decreases at the same rate of change in the power supply frequency (Fig. 3). The passage through the resonance is accompanied by a jump in the rotational velocity of the debalances, as well as a change in the type of their synchronous rotation and the jaws’ oscillation form. These effects are associated with a slip in asynchronous motors and the interaction of the oscillating system with vibration exciters.
Fig. 3The rotational speeds of debalances ωj in time τ
Fig. 4Mutual phase shift Δφ between the debalances in time τ
To analyze the possible influence of non-simultaneous contact of the jaws with the processed medium on the exciters’ synchronization and the jaws’ vibrations, the crusher’s oscillations were simulated with a gradual change in the initial gap between the left jaw and the corresponding contact element of the processed medium for a given value of power supply frequency. The gap varied in the range of –0.1 ≤ ≤ 0.4 with a step 0.1 and an exposure at each step for 400 (the law of change of the gap is shown in Fig. 5). At the same time, the initial gap between the right jaw and the right contact element of the medium did not change and, to ensure the initial contact symmetry, it was assumed to be –0.1. The study was carried out for different frequencies of the supply voltage in the range of [1.85, 2.5], in which a exciters’ synchronous antiphase rotation occurs (after the third resonance). The frequency range [0.8, 1.2] between the first and second resonances was not considered, because at these frequencies the developed forces are usually not sufficient to destroy the material, and therefore it is not used in common practice.
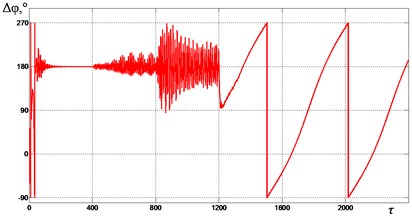
In Fig. 6-9 graphs of the change in the mutual phase shift of between the debalances obtained at supply voltage frequencies {1.85, 2.0, 2.2, 2.4} are presented. It can be seen that at frequencies {1.85, 2.0} (see Fig. 6 and Fig. 7), the exciters’ synchronization is broken when the gap 0.4 is reached. In this case, the mutual phase shift between the debalances does not stabilize with time. In turn, this leads to a violation of the required oscillation synchronous antiphase mode of the crusher’s jaws. When 2.2 (see Fig. 8), a synchronization violation occurs when 0.3. When 2.4 (see Fig. 9), synchronization is violated when 0, while the mode of antiphase oscillations of the crusher’s jaws is maintained up to 0.2 (i.e., up to 1200). Thus, with an increase in the excitation frequency, a decrease in the contact asymmetry of the processed medium with the crusher’s jaws is observed, at which a violation of the required exciters’ synchronization and, accordingly, oscillations of the jaws occurs.
Fig. 5The change in the gap δ~1 in time τ
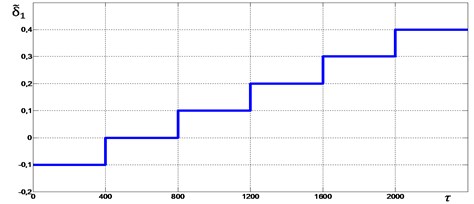
Fig. 6Mutual phase shift Δφ between the unbalances at ωe= 1.85
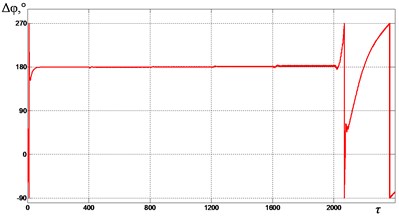
Fig. 7Mutual phase shift Δφ between the unbalances at ωe= 2.0
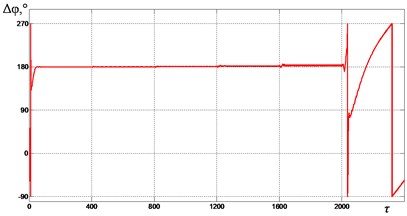
Fig. 8Mutual phase shift Δφ between the unbalances at ωe= 2.2
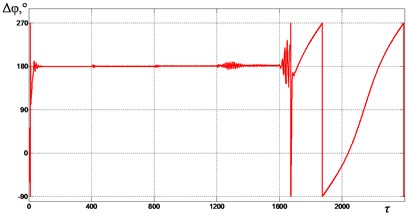
Fig. 9Mutual phase shift Δφ between the unbalances at ωe= 2.4
4. Conclusions
The simulation results presented in this paper clearly demonstrate the possibility of violation of the debalances synchronous rotation and, accordingly, oscillations of the crusher’s jaws when the contact interaction conditions with the processed medium are changed due to jaws’ non-simultaneous contact with the processed medium. It is shown that with an increase in the excitation frequency, a decrease in the contact asymmetry of the processed medium with the crusher’s jaws is observed, at which a violation of the required synchronous rotation of the unbalances and, accordingly, oscillations of the jaws occur. Such changes in the contact interaction conditions can occur directly during the crusher’s operation, and they must be taken into account when assigning its operating modes.
References
-
Blekhman I. Theory of Vibrational Processes and Devices. Vibrational Mechanics and Vibration Technics. Ore and Metals, St. Petersburg, 2013.
-
Vaisberg L., Zarogatskiy L., Turkin V. Vibrational Crushers. Bases for Design, Engineering and Technological Applications. VSEGEI, St. Petersburg, 2004.
-
Tyagushev S., Turkin V., Shonin О. Jaw crusher antiphase-locked operation stabilization by means of automatic electric drive. Obogashchenie Rud, Vol. 2, 2016, p. 38-40.
-
Blekhman I. Vibrational Mechanics. Nonlinear Dynamic Effects, General Approach, Applications. World Scientific, Singapore, 2000.
-
Vibration in Engineering: Handbook. Vol. 4, Mechanical Engineering, Moscow, 1981.
-
Arkhipov M., Vetyukov M., Nagaev R., Utimishev M. Dynamics of a vibrational crusher, taking account of the material being crushed. Journal of Machinery Manufacture and Reliability, Vol. 1, 2006, p. 15-18.
-
Nagaev R., Karagulov R. Dynamics of a vibration machine with allowance for the influence of treated material. Problemy Mashinostraeniya i Nadezhnos’ti Mashin, Vol. 1, 2001, p. 48-51.
-
Shishkin E., Safronov A. Vibratory jaw crusher dynamics with consideration of working load effect. Obogashchenie Rud, Vol. 366, Issue 6, 2016, p. 39-43.
-
Astashev V., Babitsky V., Kolovsky M. Dynamics and Control of Machines. Springer, Berlin, 2000.
About this article
The reported study was funded by RFBR according to the research project No. 18-08-01491_a.
