Abstract
Rockfall influences the safety of infrastructure and transportation lines normal operation, application of SAR technology to monitor the rockfall could predict rockfall disaster. One of the most important factors in rockfall target detection is the signal-to-clutter-plus noise ratio (SCNR) after clutter suppression, which should be maximized before rockfall target detection. Through analyzing remainder rockfall target characteristic after clutter suppression, the method of removing quadratic FM component introduced by platform velocity and along track velocity of rockfall target is proposed. After removing quadratic FM component by Dechirp technology, remainder rockfall target is focused in Doppler region image and the SCNR of remainder rockfall target is maximized. So, it has a preferable result in rockfall target detection. To resolve the contradiction between calculated amount and the accuracy of along track velocity, this paper adopts the technology of gradual approach. The effectiveness of the presented method is demonstrated by both theoretic analysis and simulated data.
1. Introduction
Rockfall influences the safety of infrastructure and transportation lines normal operation, application of SAR technology to monitor the rockfall could predict rockfall disaster. To achieve the detection and imaging of rockfall target, two problems must be settled. One is to restrain ground clutter, which should maximize SCNR of the signals of remainder rockfall targets as possible after clutter suppression to get a preferable result in rockfall target detection; the other is how to estimate parameters of rockfall targets accurately, to make focused image processing of the rockfall targets whose motion characteristics are unknown possible.
Currently, most used methods of rockfall target detection: Displaced Phase Center Antenna (DPCA), Along-track Interferometry (ATI), and Space-Time Adaptive Processing (STAP). STAP uses Space-Time adaptive processing method, which can restrain clutter and interfere, however, the computational complexity is too huge [1]. Re-STAP can solve the problem about computational complexity in STAP, but the algorithm is vulnerable to the effects of non-uniform environment [2-8]. Meanwhile, neither DPCA nor ATI can eliminate the influence of detection performance suffering the along track velocity of rockfall targets [9-18].
In order to maximize the CSNR of remainder rockfall targets signals after clutter suppression, and get a preferable result in rockfall target detection, this paper came out with a multichannel SAR rockfall detection and parameters estimation method combined with Dechirp technology to increase the SCNR of remainder rockfall target. The method is based on three-channel SAR rockfall target detection and parameters estimation. Above all, DPCA technology is used to offset clutter in data domain to get the remainder rockfall targets signals after two clutters offset; then process one of them with Dechirp, use technology of gradual approach to get remainder rockfall targets signals frequencies. After removing quadratic FM component by Dechirp technology, remainder rockfall target is focused in Doppler region image and the SCNR of remainder rockfall target is maximized, so it has a preferable result in rockfall target detection.
This paper is arranged as follows, in the second section, the model of the three channel SAR-GMTI system is analyzed; the third section is based on the second section, analyzing the characteristics of the residual rockfall target signals; in the fourth section, the principle of successive approximation; in the fifth section, the method of parameter estimation is given; the conclusion is given in the seventh section.
2. Characteristic analysis of remainder rockfall target signal
For the echo signal of channel 1 and channel 2, the time domain DPCA algorithm is used to eliminate clutter, receiving signal . In the same time, the DPCA algorithm is used to eliminate clutter in the echo signal of channel 2 and channel 3, receiving signal :
where and are phase deviations caused by compensating channel spacing:
Substitute the Eqs. (1), (2), (3) into the Eqs. (1) and (2), and finishing:
The radial velocity of the stationary target is zero, so the stationary target Eqs. (5) and (6) are equal to zero, so the DPCA algorithm can effectively suppress the clutter.
Rockfall target residual clutter suppression of SCNR directly affects the detection performance of rockfall targets, so we should make the target SCNR reach the maximum residual rockfall before falling target detection. By Eqs. (5) and (6) we can see, and , the signals of remainder rockfall targets after clutter suppression, are both LFM signals, there is only one Doppler frequency shift due to the channel spacing . Their frequency modulation is shown in Eqs. (7), related to the flight speed and the along track velocity of the rockfall target:
In order to make the clutter suppression after the residual rockfall target SCNR reached the maximum, we could apply Dechirp technology to , the signal of remainder rockfall target after clutter suppression, therefore, the Doppler frequency modulation could be removed effectively due to the motion of the carrier. Reference function, . If the rockfall along track velocity of the rockfall target is equal to zero, the Doppler frequency of the rockfall target is equal to the static one. After azimuth dechirp processing, rockfall targets in a synthetic aperture time can be considered a single frequency signal, so that the target energy in the rockfall azimuth Doppler domain focus, and the SCNR of the remainder rockfall target could reach maximum. However, the along track velocity tends to exist actually, making the Doppler frequency of rockfall target different from the static one’s, therefore, using the Doppler frequency of static target to carry out dechirp process couldn’t solve the problem of energy defocusing in along track velocity:
Apply the Doppler frequency of a static target to to process the azimuth dechirp, and we could obtain . According to Eq. (8), the signal of remainder rockfall target is still LFM signal after azimuth, as frequency is shown in Eq. (9). Therefore, after azimuth dechirp processing, the root cause of the signal of remainder rockfall target defocusing is that, the along track velocity of rockfall target differs the Doppler frequency of rockfall target from the static one’s, and the Doppler frequency of static target used in the azimuth dechirp process could not completely remove the quadratic FM component of the remainder rockfall target:
If we make use of the Doppler frequency of rockfall target in the dechirp process, the problem could be solved, so the energy of the remainders could focus, maximizing the SNCR. Apply the Doppler frequency of the remainder rockfall target to to process the azimuth dechirp, and we could obtain . Reference function is , is the received Doppler domain image after processing azimuth Fourier transform to , is the Doppler frequency, is the pulse count. As shown in Eq. (17), rockfall in Doppler domain is the target image of single frequency signal, and the energy of the target focus, whose Focusing frequency point is :
Therefore, we could apply Doppler frequency of the remainder rockfall target to to azimuth dechirp process to maximize SCNR of the rockfall target, so we can obtain a preferable detection effect.
3. Successive approximation principle
Normally, the rockfall azimuth velocity could not be accurately estimated before rockfall target detection, thus in this paper, a set of reference functions are formerly defined, each function of which corresponds a Doppler frequency , each Doppler frequency is equal to the azimuth velocity of the rockfall target . Using this set of reference functions to carry out azimuth frequency dechirp processing for , by comparing the results of the processing, we can judge the correct results, then according to the parameters of the reference function for rockfall azimuth velocity.
This method has the advantages of simple principle and simple processing steps, maximizing the SCNR of the remainder rockfall target in the process to improve the detection performance of rockfall target, and the along track velocity of the rockfall target could be obtained according to the parameters in the reference functions. However, in this paper, there is a contradiction between the computation precision and the along track velocity estimation precision, that we have to obtain a higher accuracy of Doppler frequency estimation to remainder rockfall target to obtain the higher accuracy of the along track velocity estimation , which requires the Doppler frequency difference between the reference functions must be low enough, thus increasing the computation quantity. If the probable Doppler frequency of remainder rockfall target rates in and , the frequency of dechirpproccessing required is:
In order to solve the contradiction between the computation quantity and the accuracy of the azimuth velocity estimation, this paper uses successive approximation principle for rockfall azimuth velocity. Before the successive approximation method is introduced, the influence of the frequency mismatch on the frequency modulation is analyzed. By using a set of reference functions with different frequency modulation, the ideal LFM signal is de tuned, and the power distribution of the LFM signal is eliminated as shown in Fig. 1. Relative frequency rate in Fig. 1 the abscissa, the ratio of frequency is to use when the dechirp rate and LFM signal, the vertical axis represents the frequency of the signal, each one of said longitudinal tangent using FM and the corresponding rate to FM signal after power distribution. From Fig. 1 we can see that, only the use of FM signal is consistent with the rate of the dechirp processing, can make the FM signal energy in the frequency domain focus, while FM signal deviation rate, defocusing energy decreased rapidly with the increase of deviation.
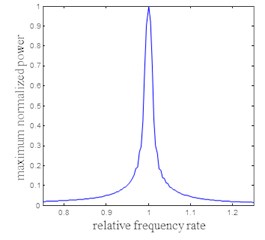
Fig. 2 is an ideal LFM signal to FM in the maximum normalized power after treatment, it can be concluded from the Fig. 4 curves, using different frequency to FM rate, maximum power signal, maximum power FM rate along the relatively symmetrical distribution, when using FM FM signal and consistent rate to FM when the maximum power signal to reach the maximum, and the deviation in FM FM signal rate, maximum power and rapid increase with the bias is reduced. Therefore, in order to reduce the amount of computation, the FM can be used the method of successive approximation used to adjust the dechirp rate.
The principle of using successive approximation to reduce the amount of computation is shown in Fig. 3. Step 1, determine the range of possible frequencies ; step 2, use the reference function of the frequency modulation rate of , , , the chirp signal is processed; step 3, the frequency modulation rate of the ideal LFM signal is adjusted by the frequency modulation rate of two larger power frequency modulation frequencies of and and the average frequency modulation rate of and , respectively; step 4, repeating step 3 can quickly approach the ideal chirp signal real frequency. , in Fig. 2.
By analyzing the principle of successive approximation, the precision of frequency modulation is obtained:
The frequency of the frequency modulation:
Supposed , according to the Eq. (13) to 500 times to FM, and according to the Eq. (15) obtained by successive approximation method after the need to 11 FM frequency so it can be concluded that in the condition of the same estimation accuracy, by successive approximation method can greatly reduce the computation quantity, so as to solve the computation with the azimuth estimation accuracy between the contradictions.
Fig. 1Power distribution of ideal LFM signal after de frequency modulation
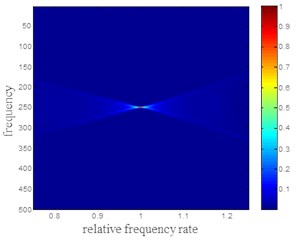
Fig. 2The maximum normalized power of ideal LFM signal after de frequency modulation
4. Simulation analysis
In order to verify the effectiveness of this method, three experiments were done in this section. System parameters are as follows, carrier speed is 250 m/s, center slant distance is 30 km, wavelength is 0.0319m, subaperture length is 1m, channel count is 3, pulse duration is 10 us, transmitting bandwidth is 100 MHz, distance sampling rate is 120 MHz, pulse repetition frequency is 576 Hz.
The target parameters of rockfall are shown in Table 1.
Supposed that the input SCNR of the rockfall target is equal to –12 dB, the probable along track velocity range is (–30 m/s, 30 m/s) (in data processing it can be adjusted according to the actual situation). By using the successive approximation principle introduced in section fourth, the target speed range to the successive approximation of rockfall according to rockfall potential target along track velocity range of real. According to the principle of successive approximation, from the first dechirp processing to the eighth, estimation to the target along track velocity of rockfall respectively is –30 m/s, 30 m/s, 0 m/s, 15 m/s, 7.5 m/s, 11.25 m/s, 9.375 m/s, 10.3125 m/s, the along track velocity error decreases rapidly with the increase of the frequency, error to speed through the rockfall target azimuth to estimate the frequency treatment is 3.125 % after the eighth dechirp processing. Therefore, the principle of successive approximation can be used to solve the contradiction between the computation quantity and the accuracy of along track velocity estimation well.
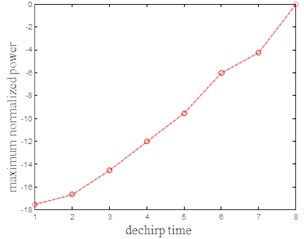
Fig. 4 is the frequency spectrum of target distance unit after dechirp processing, the successive approximation principle is used to eliminate frequency. Fig. 5 is the maximum normalized power to the target after dechirp processing, the horizontal axis shows the successive approximation principle of dechirp processing times, the vertical axis represents the maximum normalized power to the target after dechirp processing. As can be seen from Figs. 4 and 5, in the Doppler domain image, the maximum power of signal increases rapidly as the dechirp modulation times increases, the energy of the signal decreases rapidly with the increase of the frequency of the dechirp modulation. Therefore, the successive approximation principle of dechirp based on defocus energy can solve the problem of rockfall target along track velocity brings, so that the remainder rockfall target SCNR after clutter suppression as much as possible reaches the maximum.
In the Doppler domain image, defocus signal energy with increasing dechirp number decreased rapidly, when the use of FM and the residual rate of the target rockfall is approximately equal to the FM signal processing, maximum power and maximum power maximum approximation, where the frequency point is approximately equal to in the Eq. (12), the real goal of rockfall is approximately equal to the azimuthal position and radial velocity parameters according to section fifth of the estimation method to estimate the azimuthal position and velocity. Through eighth times of dechirp estimation of rockfall target azimuthal position is 40.6491 m, the radial velocity is 1.0109 m/s.
Fig. 3Successive approximation principle
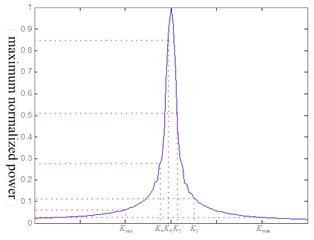
Table 1The rockfall target parameters
Radial | Azimuth | Radial | Along track | |
Position | Position | Velocity | Velocity | |
Rockfall target | 30000 m | 40 m | 1 m/s | 10 m/s |
Fig. 4Where the distance to target spectrum of rockfall unit FM after treatment
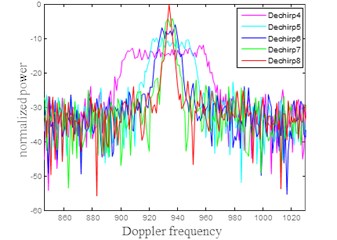
Fig. 5The maximum normalized power to FM after rockfall target
5. Conclusion
SCNR clutter on the target signal after the elimination of remainder rockfall directly affects the target detection performance of rockfall. In order to maximized the SCNR of the remainder rockfall target signal to get a preferable rockfall target detection, A novel method of dynamic monitoring and parameters estimation for rockfall based on multichannel SAR is proposed in this paper. In order to solve the contradiction between the computation quantity and the accuracy of the along track velocity estimation, this paper adopts the principle of successive approximation. Through the theoretical analysis and simulation, it can be concluded that the proposed method could effectively increase the SCNR of remainder rockfall target signal and make a good target detection effect even when the input SCNR is small. In addition, under the presence of multiple targets in the same range, this method still has a good target detection results and parameter estimation accuracy of rockfall.
References
-
Ender H. G. Space-time processing for multichannel synthetic aperture radar. Electronics and Communication Engineering Journal, Vol. 11, Issue 1, 1999, p. 29-38.
-
Baumgartner Stefan V., Krieger Gerhard A priori knowledge-based post-doppler STAP for traffic monitoring applications. IEEE International Geoscience and Remote Sensing Symposium, 2012, p. 6087-6090.
-
Rosenberg Luke, Gray Douglas A. Constrained fast-time STAP for interference suppression in multichannel SAR. IEEE Transactions on Aerospace and Electronic Systems, Vol. 49, Issue 3, 2013, p. 1792-1805.
-
Gracheva V., Cerutti Maori D. Multi-channel analysis of sea clutter for STAP applications. 9th European Conference on Synthetic Aperture Radar, Germany, 2012.
-
Cristallini Diego, Bürger Wolfram A robust direct data domain approach for STAP. IEEE Transactions on Signal Processing, Vol. 60, Issue 3, 2012, p. 1283-1294.
-
Cristallini Diego Target DOA estimation based on robust deterministic STAP. 9th European Conference on Synthetic Aperture Radar, Germany, 2012.
-
Cerutti Maori D., Sikaneta I. Optimum GMTI processing for space-based SAR/GMTI systems-theoretical derivation. 8th European Conference on Synthetic Aperture Radar, Germany, 2010.
-
Yan He, Zheng Ming-Jie, Li Fei, et al. A new clutter plus noise spectral density matrix estimation method in wide area surveillance mode. Journal of Electronics and Information Technology, Vol. 33, Issue 12, 2011, p. 2852-2857.
-
Van Trees Harry L. Detection, Estimation, and Modulation Theory: Radar Sonar Processing and Gaussian Signals in Noise, Part III. Wiley-Interscience, New York, 2001.
-
Yan H., Robert W., Li F. Ground moving target extraction in a multichannel wide-area surveillance SAR/GMTI system via the relaxed PCP. IEEE Geoscience and Remote Sensing Letters, Vol. 10, Issue 3, 2013, p. 617-623.
-
Zheng Mingjie, Yang Ruliang SAR moving targets detection based on DPCA and interferometric processing. Journal of Electronics and Information Technology, Vol. 25, Issue 11, 2003, p. 1525-1530.
-
Zheng Mingjie, Yang Ruliang Dual channels along-track interferometry SAR ground moving target detection. Journal of Electronics and Information Technology, Vol. 27, Issue 10, 2005, p. 1560-1563.
-
Zheng Shi-Chao, Song Hong-Jun, Yiuya Bo, et al. Error analysis of fast-moving target geo-location in wide area surveillance ground moving target indication mode. Journal of Radars, Vol. 2, Issue 4, 2013, p. 445-453.
-
Zheng Ming-Jie, Yan He, Zhang Bing-Chen, et al. A novel method of moving target detection and parameters estimation for bi-channel WAS radar based on DBS image. Journal of Radars, Vol. 1, Issue 1, 2012, p. 36-42.
-
Yan He Study on Airborne Wide-area Moving Targets Surveillance. Chinese Academy of Sciences Institute of Electronics, Beijing, 2013.
-
Chen Peng, Wu Lenan Compressive sensing for multi-carrier EBPSK radar. Journal of Southeast University: Natural Science Edition, Vol. 44, Issue 1, 2014, p. 23-27, (in Chinese).
-
Li Jing, Xuechengqi, Shi Minghao, et al. Information visual structure based on multidimensional attributes of information. Journal of Southeast University, Natural Science Edition, Vol. 42, Issue 6, 2012, p. 1094-1099, (in Chinese).
-
Lai J., Mao S., Qiu J., et al. Investigation Progresses and Applications of Fractional Derivative Model in Geotechnical Engineering. Mathematical Problems in Engineering, Vol. 2016, 2016, p. 9183296.
