Abstract
This paper presents a numerical study on the dynamic responses of the non-ballast track structures under the high-speed train load that is excited by the rail irregularity at the welded rail joint. In this study, a multi-body dynamics model with 10 degrees of freedom is built to model a high-speed vehicle and a finite element model is established to simulate the non-ballast track. A mathematical model is also given to characterize the geometry of the local rail irregularity at the welded rail joint. By coupling the high-speed vehicle model and the track model and taking the mathematical model of the welded rail joint as an input, the dynamic responses of the non-ballast track structures under a rail vehicle running at a high speed are simulated and discussed in this paper. The wheel/rail force and the rail and slab vibration acceleration are investigated to demonstrate the significant dynamic effects on the track structures due to the welded rail joint.
1. Introduction
The continuous welded rail track has been extensively adopted in railways all over the world for a long time [1]. Relative to the conventional rail tracks, the continuous welded rail track significantly decreases the local track irregularity at the rail joints by welding the rail segments which helps distinctly mitigate the dynamic effects of the running trains and therefore benefits the track maintenance and service life. Owing to its advantages, the welded rail track is strongly recommended to be adopted in the high-speed railways [2].
However, the trains running on the high-speed railways are quite sensitive to the track irregularities especially those with short wavelength [3, 4]. Even the irregularity with a pretty small amplitude and a short wavelength probably results in distinct dynamic effects to the high-speed trains and the railway track. Although the welded rail joints provide much better rail surface transition between adjacent rail segments relative to the conventional joints, there are still local rail irregularities at the welded rail joints [5]. Those local irregularities always have very short wavelength and small amplitudes. Hence, when the welded rail track is used in the high-speed railways, the dynamic effects that the local rail irregularities at the welded rail joints have on the high-speed trains and track structures should be carefully investigated.
In this paper, a multi-body dynamics model is firstly built to model a high-speed vehicle. In the meanwhile, a finite element model is presented to model the non-ballast track. Then, a mathematical model is also generated to represent the geometry of the local rail irregularity at the welded rail joint. Through the dynamic simulations, the dynamic responses of the non-ballast track structures when a rail vehicle passing a welded rail joint area at a high speed are simulated and discussed.
2. Dynamics model
2.1. Dynamics model of a high-speed vehicle
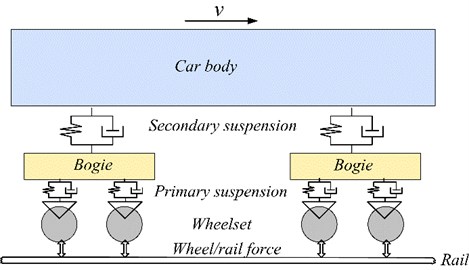
A large number of published studies have developed various dynamics models for the rail vehicles such as the half vehicle model, the complete vehicle model and the three-dimensional spatial dynamics model [6]. In this study, a vertical dynamics model with 10 degrees of freedom (DOFs) is built for the high-speed vehicle based on the theory of the multi-body system dynamics. Fig. 1 illustrates the schematic drawing of the vertical dynamics model of a high-speed vehicle. In this mode, the car body, two bogies and four wheelsets are represented using mass blocks. All of these mass blocks can move up and down along the vertical direction. Also, the car body and two bogies can rotate in the vertical plane. The spring-dampers are used to connect each mass block to simulate the primary and secondary suspensions in the high-speed vehicle.
According to the Newton’s second law, the dynamics equations for the high-speed vehicle model can be expressed as:
where means the vector of the 10 DOFs in the vehicle, , and represents the mass, damping and stiffness matrix of the multi-body system. The symbol is the load vector applied to the vehicle which is actually the contribution of the dynamic interaction forces between wheelsets and the rail. The wheel/rail forces can be calculated according to the non-linear Hertz contact theory where the effect of the rail irregularity is also taken into account.
Fig. 1Schematic drawing of the dynamics model of a high-speed vehicle
2.2. Dynamics model of a non-ballast track
The mechanical models for non-ballast track are also described in many other studies [7]. In this paper, a finite element model is established for the non-ballast track. Fig. 2 shows the schematic drawing of the finite element model of the non-ballast track. In this model, the rails, the concrete slabs, the supporting layer and the concrete base with real geometry sizes in the track are all modelled using hexahedral solid elements. The rail pads under the rail are modelled using the spring-dampers. The mechanical parameters of each component in the finite element model such as the density, the Young’s modulus and damping are chosen according to the material properties of the field track structures. The vibration modes of the track model are firstly solved and then they are used to simulate the dynamics responses of the track under external loads with the modal superposition method.
3. Mathematical model of the rail irregularity at a welded rail joint
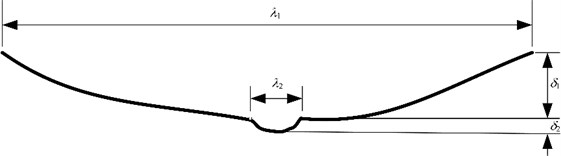
The track irregularities at different welded rail joints are very complex due to the influences of the welding process, technology and environment. Nevertheless, the local rail surface irregularity at a welded rail joint along the rail direction can be simply described using a mathematical model as illustrated in Fig. 3. The local rail irregularity at a welded rail joint can be regarded as a larger cosine wave with a longer wavelength of and a larger amplitude of . At the center of the larger cosine wave, there will be a smaller cosine wave with a shorter length of and a smaller amplitude of . When a train passes the welded rail joint area at a high speed, both the larger and smaller cosine waves will cause distinct dynamic effects to the trains and the track structures. The wavelength and amplitude parameters of the welded rail joint model in this study are chosen according to previous field measured results.
Fig. 2Finite element model of the non-ballast track
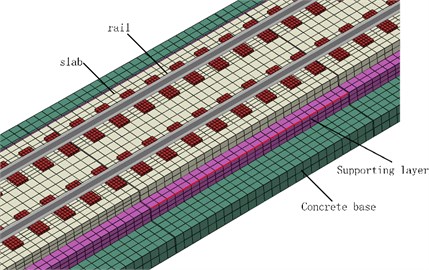
Fig. 3The mathematical model of the rail irregularity at the welded rail joint
4. Dynamic responses
Utilizing the dynamics models for the high-speed vehicle and the non-ballast structure and taking the mathematical model of the track irregularity at the welded rail joint as an input to the dynamics models, the dynamic responses of a non-ballast structure are successfully simulated when a high-speed vehicle running at a speed of 200 km/h passes the rail area with a welded joint. The results of the dynamic responses will be presented in Figs. 4-6 and discussed in this section. All the results are comparable to those in other literatures which indicates that the dynamics models and the responses presented in the paper are reasonable.
Fig. 4 presents the time history of the dynamic wheel/rail force induced by the rail irregularity at the welded rail joint. It can be seen that the wheel/rail force increases dramatically to 250 kN due to the excitation of the welded rail joint. It is almost as 5 times as the static wheel load. This dynamic amplification effect is so significant which is very harmful to the safety of the running trains and the track structures.
Fig. 5 shows the time history of the rail vibration acceleration induced by the high-speed vehicle load at the welded rail joint area. The maximum vibration acceleration of the rail exceeds 2600 m/s2 and then attenuates to zero in a short time due to the damping effect of the rail substructures. This large rail vibration acceleration is apparently caused by the large dynamic wheel/rail force as shown in Fig. 4 which is induced by the welded rail joint.
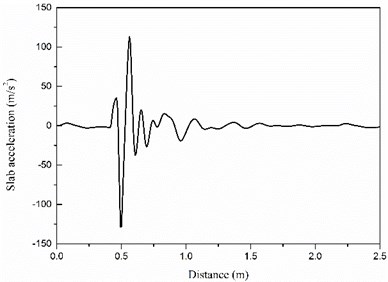
Fig. 6 further demonstrates the time history of the slab vibration acceleration induced by the high-speed vehicle load at the welded rail joint area. The maximum vibration acceleration of the concrete slab does not reach a value as large as that of the rail, but it still reaches around 125 m/s2. Regarding the stability of the concrete material and the dynamic load transmitted from the rail to the slab is much smaller than the wheel/rail force, the vibration acceleration of the slab is also very violent.
Fig. 4Dynamic wheel/rail force induced by the rail irregularity at the welded rail joint
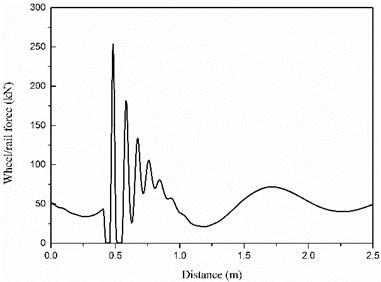
Fig. 5The rail vibration acceleration under the high-speed train load at the welded rail joint
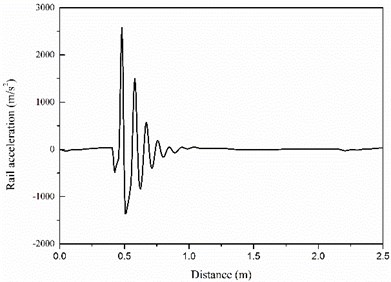
Fig. 6The slab vibration acceleration under the high-speed train load at the welded rail joint
5. Conclusions
The welded rail joints may cause distinct dynamic effects to the trains and the track structures when they are applied to the high-speed railways. This paper presented a integrate dynamics model for the high-speed vehicle and non-ballast track based on the multi-body system dynamics and the finite element method. A simple mathematical model is also generated to simply simulate the rail irregularity at a welded rail joint and incorporated into the dynamics model of the rail vehicle and track. Through the dynamics simulations in the paper, the results demonstrate that when a rail vehicle passes the rail area with a welded joint at a high speed of 200 km/h, the dynamic effects induced by the welded joint are so significant that the dynamic wheel/rail force, the vibration acceleration of the rail and the slab increases dramatically. These large forces and vibration acceleration are very harmful to the safety of the trains and may cause damage problems to the track structures. This study indicates that careful maintenance such as periodically grinding to the welded rail joint is necessary for the high-speed railways if the continuous welded rail track is adopted.
References
-
Lim N. H., Park N. H., Kang Y. J. Stability of continuous welded rail track. Computers and Structures, Vol. 81, Issue 22, 2003, p. 2219-2236.
-
Cheng J., Jia F., Wang J. Key techniques of ballastless track design on high-speed railway. China Railway Science, Vol. 25, Issue 2, 2004, p. 42-47.
-
Zhai W., Cai C., Wang Q., Lu Z., Wu X. Dynamic effects of vehicles on tracks in the case of raising train speeds. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, Vol. 215, Issue 2, 2001, p. 125-135.
-
Madshus C., Kaynia A. M. High-speed railway lines on soft ground: dynamic behaviour at critical train speed. Journal of Sound and Vibration, Vol. 231, Issue 3, 2000, p. 689-701.
-
Luo C. X., Wang S. G., Zhai W. G. Microstructure and Mechanical Properties of Welded Joint of 6082 Aluminum Alloy for Rail Transportation. Electric Welding Machine, 2011.
-
Jin X. A 3D model for coupling dynamics analysis of high-speed train/track system. Zones of International Friction, North America, South of the Great Lakes Region, 2015, p. 1748-1754.
-
Zhang N., Zhou S., Xia H., Lu S. Evaluation of vehicle-track-bridge interacted system for the continuous crts-ii non-ballast track slab. Science China Technological Sciences, Vol. 57, Issue 10, 2014, p. 1895-1901.
