Abstract
The primary objective of the study is analytically predicting the anti-vibration coating on the handles and to evaluate the vibration isolation effectiveness. The ISO 10068:2012 two-point driving human physical models are coated with Foam-A material, Foam-B material, and Gel material. The coated ISO models are applied to predict the effectiveness of three different anti-vibrations coating in terms of vibration transmitted to the finger, palm, and the shoulder. The results are obtained as a vibration transmissibility magnitude in the three orthogonal directions (, , ) and the results are also compared with uncoated models. A significant level of vibration reductions was found. The proposed model may also be useful for further analysis of anti-vibration coating materials and help designers to develop better handles for vibrating tools.
Highlights
- ISO models are applied to predict the effectiveness of three different anti-vibrations coating in terms of vibration transmissibility
- The proposed model may also be useful for further analysis of anti-vibration coating materials
- Help designers to develop better handles for vibrating tools
1. Introduction
Hand operating tools such as drills, grinders, road breakers are highly transmitting large magnitude of vibration to the hand-arm system. The vibration transmitted to the hand-arm system leads to hand-arm vibration syndrome (HAVS) [1]. The bio-dynamic properties of the hand-arm system are based on the vibrating tool and the dynamic behavior of the tool or machine. To understand the mechanisms behind vibration-induced disorders, the bio-dynamic responses of the hand-arm system is to be considered and effective knowledge is required for the better development of assessing the vibration risk [2, 3]. The influence of grip force and amplitude of vibration is quantified when the system subjected to sinusoidal excitations using the driving point mechanical impedance technique (DPMI) [4]. The range of mechanical equivalent and mechanical impedance models of the hand-arm system for three orthogonal directions (, and ) are set by the international organization for standardization [5, 6]. Most of the research studies have considered vibration excitation at a single point in the hand-handle interface for deriving the driving-point bio-dynamic response data [7, 8]. The anti-vibration gloves can be used to reduce the vibration exposure and essentially serve as a simple active suspension system between the hand and the tool [9].
The deficiency of the single point approach has been overcome by two point approach method. In this approach, the hand-handle interface is separated into two distinct driving points which are palm and finger [10]. Lumped parameter models of the hand-arm system have been proposed to simulate the distributed vibration response and to estimate the power absorptions among the sub-structures of the system [11]. Two-point model and lumped parameter model provide a better estimation of the vibration transmissibility while using vibration reducing gloves [9]. These two-point coupling models have been adopted in a proposed revision of the ISO standard [5]. Most of the researchers established two-point hand coupling approach for studying the distributed responses along the forearm direction () of the system [11]. The limited experimental study is available in bio-dynamic response in finger and palm of the hand in the and orthogonal to the forearm direction [12]. One of these models has been used to evaluate the absorbed power across the substructures of the hand-arm system along forearm direction [13]. Most of the authors expanded the two point coupling hand model with more degree of freedom to predict the response in the arm-shoulder substructures [14].
This study primarily aims to predict the vibration response of the hand-arm system while using different anti-vibration coating to the vibrating tools or machines. Two point coupling human physical ISO models with, 4 DOF and 5 DOF was added with additional 2 DOF using damping materials for coatings, such as foam-A material, foam-B material and gel material and the vibration transmissibility was predicted on the orthogonal directions of the hand arm system. The results are used to identify the bio-dynamic response and to understand the associations with the dynamic properties of the hand-arm system.
2. Methods
2.1. Hand-arm system model with anti-vibration coating
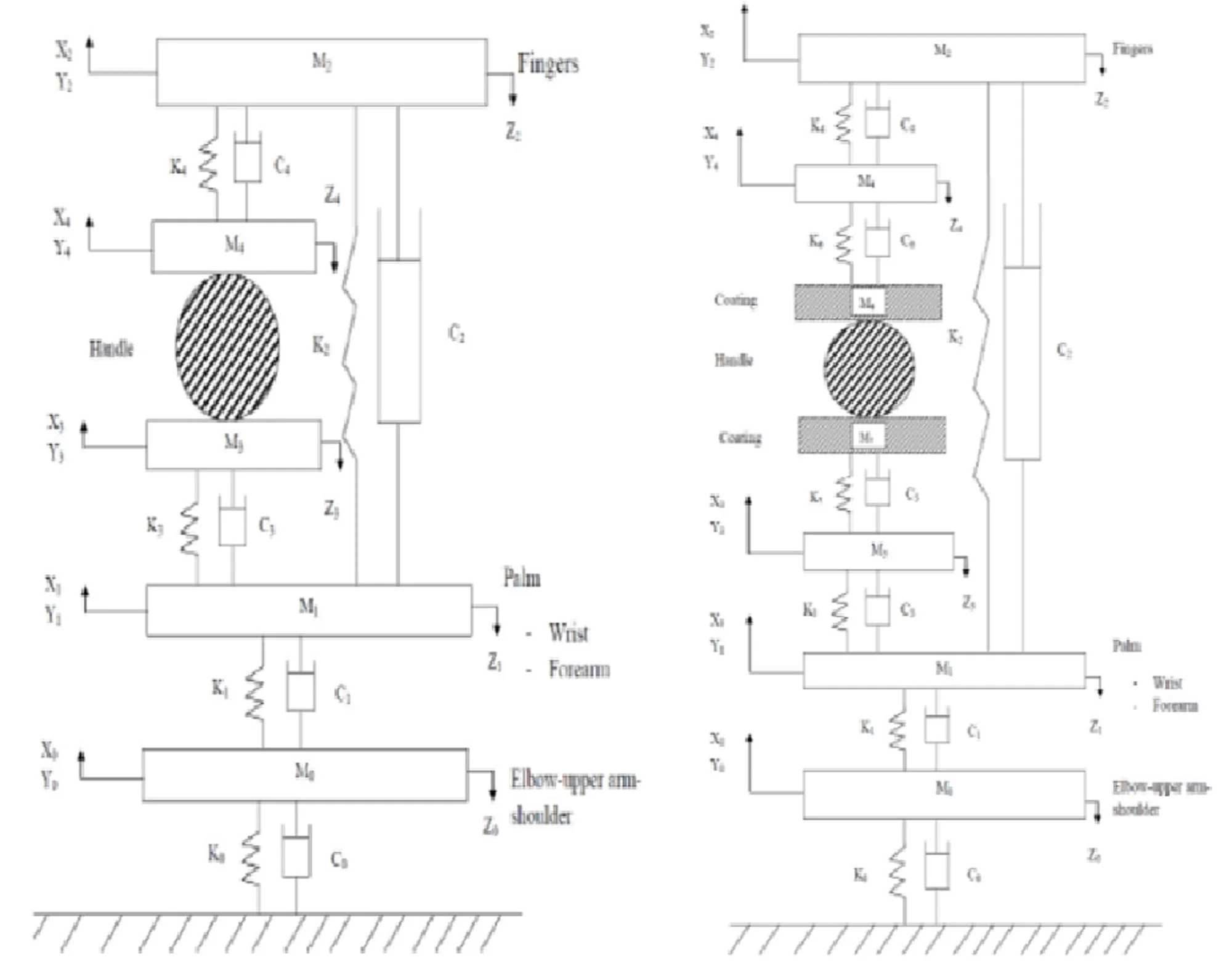
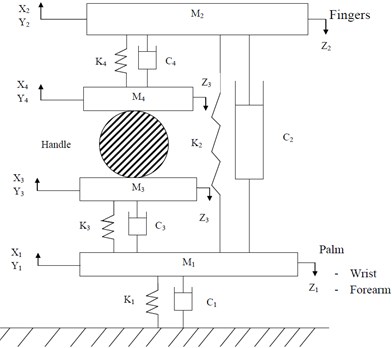
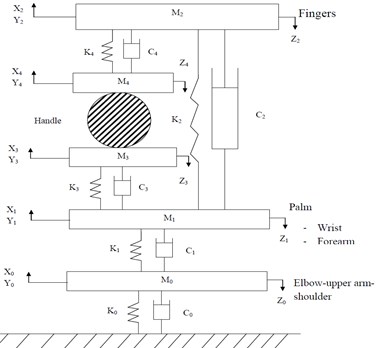
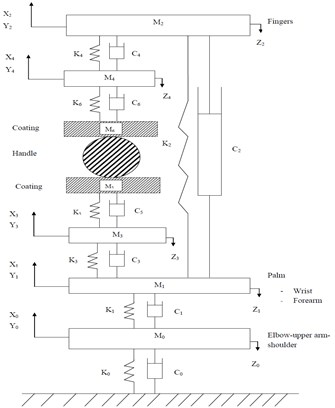
The synthesis of the ISO 10068:2012 based human physical models and the tool model for the , and directions annex-B (model-I) and annex-C (model-II) are shown in Fig. 1. Both of the human physical models are assumed as two point coupling between hand and the handle. The vibrating handle is gripped by the hand and considered as a clamp like mechanical system. The human physical model system is divided into two major parts. The Fig. 1(a) comprises the first part of the palm-wrist-forearm with substructures and is represented by two effective masses and coupled through linear stiffness , and viscous damping , . The second part constitutes the finger; finger tissues and finger bones positioned on another side of the handle and is represented by two masses and coupled through spring damping elements , and , . Another human hand physical model is shown in Fig. 1(b). It is similar to the first model except for the additional elements mass is coupled to the fixed ground through another spring damping element and .
Fig. 1Configurations of the human physical models for the xh, yh and zh directions ISO 10068: 2012: a) human physical model-I (Annex-B), b) human physical model-II (Annex-B)
a)
b)
To reduce the bio dynamic effect to the human hand-arm system the handle is coated with foam-A, foam-B and gel. In Fig. 2(a) and Fig. 2(b), the and represents the effective mass of coating materials coupled through spring damping elements , and viscous damping , . The stiffness and damping properties of the coating materials are opted from previous research [15]. The hand-arm system model is simulated to evaluate the bio-dynamic responses under vibration along the , and directions. Assuming coating material masses are not considered as degree-of-freedom because the masses are fixed to the handle in both the models. The equations of motion of the system subjected to the handle excitation are expressed in the matrix form as Eq. (1):
where [] is mass matrix, [] is damping matrix, [] is stiffness matrix, is forcing vector and is vector response coordinates.
Fig. 2Configurations of the human physical models for the xh, yh and zh directions with coating: a) human physical model-I (Annex-B) with coating, b) human physical model-II (Annex-C) with coating
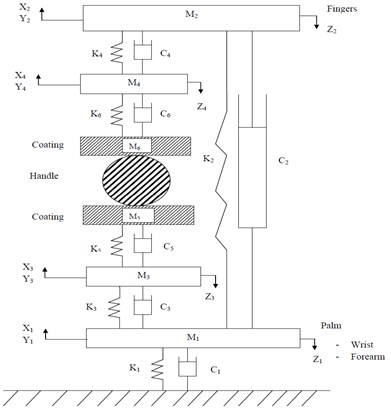
a)
b)
2.2. Frequency domain method
The equations of motion are solved using frequency domain (FD) to determine the vibration response of different substructures considered in the model. Since the response of the model depends on the frequency and the model is considered as a linear system with harmonic excitation FD method is used. By performing a Fourier transformation on Eq. (1) the following matrix form of Eq. (2) can be obtained:
where and are the complex Fourier transformation vectors of and , respectively, in Eq. (2), and is the excitation frequency. Vector contains complex displacement responses from the mass segments as a function of .
2.3. Transmissibility
The vibration response is determined using the vibration transmissibility of different substructures in the model. The vibration transmissibility, (), is a complex function given by Eq. (3):
3. Results and discussion
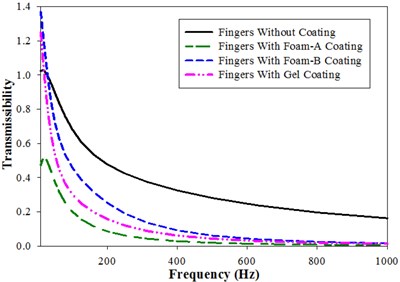
The equation of motion of the proposed model is solved to determine the bio-dynamic response of the hand-arm models. Fig. 3-7 illustrates the bio-dynamic response characteristics of the elbow-shoulder, palm, and fingers in for three orthogonal directions (, , ). The results are obtained in the ISO 10068-2012 human physical models (Annex-B and Annex-C) are compared with the coated models as a center frequency of 1/3-octave bands in the 10-1000 Hz range. Fig. 3 shows the bio-dynamic response in terms of vibration transmissibility of fingers in , and direction. Fig. 3(a) displays the comparison of the magnitude of the vibration transmissibility in the -direction for fingers without coating and with a coating of Foam-A, Foam-B and Gel. The fingers without coating and with Foam-A coating exhibit resonance at a frequency of 16 Hz, whereas, fingers with Foam-B and gel coating shows no peak. Fingers coated with Foam-B and Gel initially showed higher magnitude of transmissibility than fingers without any coat up to a frequency of 31.5 Hz and 16 Hz respectively. Then, the magnitude for coated fingers keeps on reducing at a higher rate than uncoated ones for the whole range.
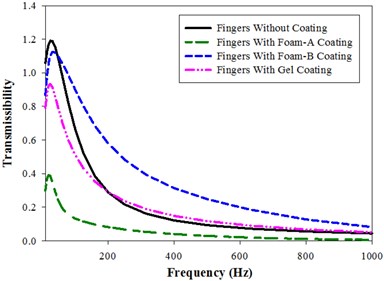
The variation of the transmissibility ratio in y-direction with a frequency for fingers without coating and with a coating of Foam-A, Foam-B and gel are shown in Fig. 3(b). In contrast to direction, magnitude peaks are observed here in all the cases. The peaks for all the four cases are obtained from 20 Hz to 40 Hz with the uncoated fingers having the highest peak with a transmissibility magnitude of 1.19 at 25 Hz. In contrast to in -direction, Foam-B and Gel coated fingers initially exhibit lower transmissibility ratio than the uncoated fingers up to a frequency of 40 Hz and 31.5 Hz respectively.
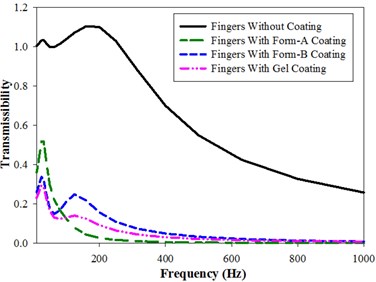
Fig. 3Vibration transmissibility of fingers (Model-I) in x, y and z direction: a) x-direction, b) y-direction, c) z-direction
a)
b)
c)
In -direction, the comparison of the magnitude of transmissibility for fingers without and with different coatings is expressed in Fig. 3(c). Here, two resonance peaks observed in all the cases except Foam-A coated fingers which exhibits a single peak. The first peak of all the cases occurs at resonant frequencies of 25 Hz and 31.5 Hz. The second peak for coated fingers occurs at a frequency of 125 Hz. The second peak of uncoated fingers exhibits the highest magnitude of transmissibility with a value of 1.10. Unlike in other axes, Foam-A coated fingers have a higher magnitude of response than Foam-B and Gel coated fingers up to a frequency of 100 Hz and 125 Hz respectively
Fig. 4 shows the bio-dynamic response in terms of magnitude of Vibration transmissibility of Palm in , and direction. There are no peaks observed for both coated and uncoated palm. Foam-B and Gel coated fingers show higher transmissibility values than the uncoated fingers up to a frequency of 20 Hz and 16 Hz respectively. Foam-B coated palm displays higher transmissibility ratios than gel coated palm till a frequency of 200 Hz, but above 200 Hz Gel coated palm values are higher than the former. Foam-A coated palm show lower values of response than all the other coated palms till a frequency of 200 Hz. After 200 Hz, the values of all the coated palms are almost equal. The analytical study results were in good agreement with the experimental study conducted by Tony et al. [16].
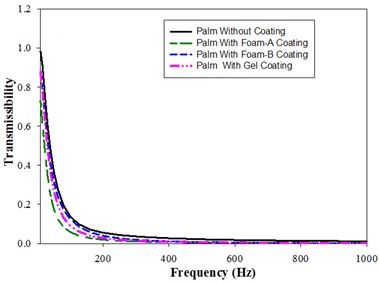
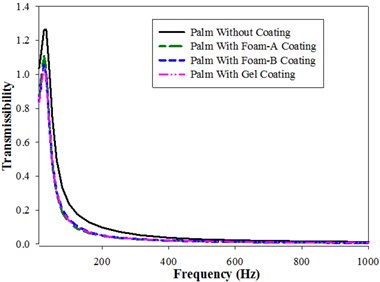
Fig. 4Vibration transmissibility of palm (Model-I) in x, y and z direction: a) x-direction, b) y-direction, c) z-direction
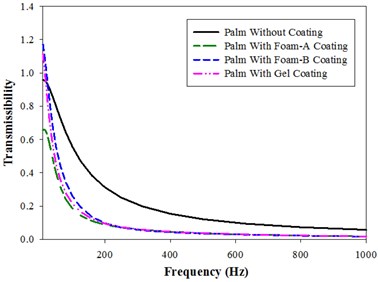
a)
b)
c)
The change in magnitude of transmissibility with frequency in y-direction for Coated and uncoated palms is shown in Fig. 4(b). The ratio of transmissibility decreases with increase in Frequency. As expected, uncoated palm shows the highest values of transmissibility followed by Foam-B and Gel coated palm. Foam-A coated palm provides higher damping than all the other coatings as inferred from its lower transmissibility values. Comparison of transmissibility ratios with frequency in -direction for uncoated and Foam-A, Foam-B and Gel coated palm is depicted in Fig. 4(c). The peaks are obtained at a resonance frequency of 25 Hz and 31.5 Hz for coated and uncoated palms respectively. At resonance conditions, uncoated palm shows the highest transmissibility of 1.3 followed by Foam-A, Foam-B and Gel coated palms respectively.
4. Conclusions
Characteristics of the Hand-arm system with different coatings on a handle were presented in this study. Because of the coating on the ISO 10068: 2012 model (annex-II) the vibration transmitted to the fingers and palm are effectively reduced in the -axis, and followed by -axis and -axis. ISO 10068: 2012 model (annex-III) vibrations transmitted to the finger, palm, and shoulder was not effectively controlled during 10 Hz to 100 Hz in all the three axes. But above 100 Hz vibration reduction has been found in the finger, palm, and shoulder in , and axes. In both the models the vibration was effectively controlled above 100 Hz. So, the low frequency vibration is very difficult to reduce using the anti-vibration of coating over the handles.
References
-
Griffin M. J. Handbook of Human Vibration. Academic Press, London, 1990.
-
Dong R. G., Wu J. Z., Welcome D. E. Recent advances in bio-dynamics of hand-arm system. Industrial Health, Vol. 43, Issue 3, 2005, p. 449-471.
-
Griffin M. J. Foundations of hand-transmitted vibration standards. Nagoya Journal of Medical Science, Vol. 57, 1994, p. 147-164.
-
Gurram R., Rakheja S., Gouw G. J. Mechanical impedance of the human hand–arm system subject to sinusoidal and stochastic excitation. International Journal of Industrial Ergonomics, Vol. 16, 1995, p. 135-145.
-
ISO-10068. Mechanical Vibration and Shock-Free, Mechanical Impedance of the Human Hand-Arm System at the Driving Point. International Organization of Standard, Geneva, Switzerland, 1998.
-
ISO-10068/DIS. Mechanical Vibration and Shock-Free, Mechanical Impedance of the Human Hand-Arm System at the Driving Point. International Organization of Standard, Geneva, Switzerland, 2012.
-
Abrams C. F., Suggs Jr Mechanical impedance simulation of vibrational characteristics of the hand-arm system. American Society of Agriculture Engineers, Vol. 10, Issue 1, 1970, p. 523-570.
-
Besa A. J., Valero F. J., Suner J. L., Carballeira J. Characterisation of the mechanical impedance of the human hand-arm system: the influence of vibration direction, hand-arm posture and muscle tension. International Journal of Industrial Ergonomics, Vol. 37, Issue 3, 2007, p. 225-231.
-
Dong R. G., Mcdowell T. W., Welcome D. E., et al. Analysis of anti-vibration gloves mechanism and evaluation methods. Journal of Sound and Vibration, Vol. 321, 2009, p. 435-453.
-
Dong R. G., Wu J. Z., Mcdowell T. W., Welcome D. E., Schopper A. W. distribution of mechanical impedance at the fingers and the palm of human hand. Journal of Biomechanics, Vol. 38, Issue 5, 2005, p. 1165-1175.
-
Dong R. G., Dong J. H., Wu J. Z., Rakheja S. Modeling of biodynamic responses distributed at the fingers and the palm of the human hand-arm system. Journal of Biomechanics, Vol. 40, Issue 10, 2007, p. 2335-2340.
-
Dong R. G., Welcome D. E., Xu X. S., Warren C., Mcdowell T. W., Wu J. Z., Rakheja S. Mechanical impedances distributed at the fingers and palm of the hand-arm system in three orthogonal directions. Journal of Sound and Vibration, Vol. 331, 2012, p. 1191-1206.
-
Dong J. H., Dong R. G., Rakheja S., Welcome D. E., Mcdowell T. W., Wu J. Z. A method for analyzing absorbed power distribution in the hand and arm substructures when operating vibrating tools. Journal of Sound and Vibration, Vol. 311, 2008, p. 1286-1309.
-
Adewusi S., Rakheja S., Marcotte P. Biomechanical models of the human hand-arm to simulate distributed biodynamic responses for different postures. International Journal of Industrial Ergonomics, Vol. 42, 2012, p. 249-260.
-
Rezali Khairil Anas Md, Griffin Micheal J. Transmission of vibration through gloves: effects of material thickness. Ergonomics, Vol. 59, Issue 8, 2015, p. 1026-1037.
-
Jain A. R. Tony B., Alphin M. S. Assessment of ergonomically designed handle shapes for low-frequency vibration responses. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, https://doi.org/10.1177/1464420718766961.
