Abstract
The aim of this article is to present universal multibody dynamic model of the heavy commercial vehicle equipped with direct yaw moment control system. The presented simulation method is based on interconnection of the multibody software ADAMS and the graphical programming environment MATLAB Simulink. The main task is to demonstrate the potential effects of the direct yaw moment control using an active differential by heavy commercial vehicle with rear wheel drive.
1. Introduction
The technology of the yaw moment control systems is commonly used since 1990s and became a standard equipment of the personal vehicles in the market. These systems are usually brake based electronic stability control programs (ESP) which stabilize the vehicle in limit situations. However, brake-based systems have the main disadvantage, that they reduce the speed performance of the vehicle. With the increasing performance of the modern vehicles, manufacturers need to ensure vehicle stability and controllability also during fast maneuvers. Mainly because of this reason, are also the technologies of powertrain torque management increasingly developed during last two decades. Beside the use of front-back torque control couplers as BMW xDrive or Haldex coupling, are the active right-left torque control systems as Honda SH-AWD or Mitsubishi AYC investigated [1]. However, these technologies are developed for personal cars only and the application to heavy commercial vehicle is missing. From the viewpoint of heavy commercial vehicles, it is obvious that the manufacturers have the primarily target in systems reliability and operational efficiency and the new technologies development is very conservative. However, also for heavy commercial vehicles could be the right-left active yaw control technology significantly advantageous. Example of such a dynamic state is described on the multibody heavy commercial vehicle model further in this article.
Multibody method of the mechanism simulation is a commonly used tool for complex mechanisms analysis and it is suitable for various types of tasks from handling robots to agricultural machinery [2]. Several commercial multibody programs have specialized packages for simulations of the complete vehicles and vehicle subsystems. One of the world’s most widely used solution in the field of linking multibody system and the vehicles dynamics theory is software MSC ADAMS Car. This article describes method of the ADAMS Car model interconnection with active yaw moment control algorithm in MATLAB Simulink for the analysis of right-left torque control effect on vehicle dynamic states.
2. Active yaw moment control
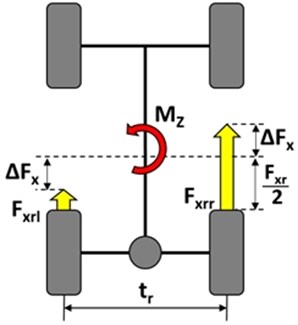
Active yaw moment control system technology with active differential creates longitudinal force differences () between left and right wheels and thereby can directly control the yaw moment () acting on a vehicle (Fig. 1). That means that tire longitudinal forces are controlled and because of this the vehicle’s cornering performance is enhanced. The advantages of these kinds of systems are that they are not based on the vehicle brakes, so they are not in violation with the driver’s acceleration and braking demands. Equally, there is nearly no change in the total driving or braking forces of both wheels. For this purpose, a lot of mechanisms of the active differentials were developed which are based on the additional gears between differential cage and the output shafts. For the smooth control of the torque difference usually two friction or electromagnetic clutches are used.
The additional yaw moment from longitudinal forces difference is defined as follows:
Fig. 1Active yaw moment control scheme: Mz – additional yaw moment, ∆Fx – longitudinal forces difference, tr – rear axle track, Fxrl, Fxrr – rear left and rear right wheel longitudinal force, Fxr – rear axle longitudinal force
3. Dynamic model
The complete simulation is based on ADAMS and Simulink co-simulation technique and therefore consists of two main parts. First part is the complete vehicle multibody model built in MSC ADAMS Car and second part is the attached active yaw moment control algorithm built in MATLAB Simulink. The ADAMS and Simulink cooperation method is suitable for mechatronics system development where the control algorithm regulates complex mechanical structure as robot, manipulator or car.
3.1. Vehicle model
The simulated commercial vehicle is a two-axle off-road tipper with permanent rear-wheel drive. The chassis consists of rigid “backbone” tube with independent swinging half-axles. Front suspension is formed by two air-springs and two dampers, rear suspension is equipped with two air-springs with additional coil springs and antiroll bar. Frame with “backbone” tube, cabin, tipper body and accessories (bumper, fuel tanks etc.) is modeled as one rigid part to which the load representing part is fixed. Powertrain subsystem is represented by engine block part and driveline shafts. Between the engine block part and rear axle input shaft acted a torque whose value is calculated from throttle and clutch position, engine torque curve and actual gear ratio. Between output shafts of the classic differential additional torque is acting for simulation of the active right-left torque distribution. This torque represents the active differential which directly influences tire longitudinal force difference () and it is managed by control algorithm in Simulink. The rear drive axle is equipped by dual wheels. In the multibody simulation of the complete vehicle plays important role the appropriate tire model. So, in this case the PAC2002 tire model which is suitable for vehicle handling simulation on an even road is used. This tire model was developed on the base of Magic Formula 6.2 tire model, but it is adapted by MSC software company for ADAMS Car simulations. The tire model is simulated in mode including combined force-moment calculation with relaxation behavior.
For the handling simulations it is necessary to connect the dynamic model with so called vehicle test-rig. In this case ADAMS MDI-SDI Testrig which contains driver algorithm and predefined vehicle tests is used.
Fig. 2Graphical representation of the dynamic vehicle model

3.2. Control algorithm
The used control algorithm of the active yaw control system has hierarchical structure shown in Fig. 3. Sensor inputs for upper controller which ensures desired yaw torque calculation are wheel speeds, lateral acceleration, yaw rate and steering angle. Objective of the upper controller is to keep the yaw stability of the vehicle. The aim of lower controller is estimation of the right-left torque difference which produce the desired yaw torque so as to track the target yaw rate. The desired yaw rate for yaw torque estimation is calculated as follows [4]:
where:
– desired yaw rate,
– vehicle longitudinal velocity,
, – vehicle center of gravity distance from front and from rear axle,
– vehicle mass,
, – cornering stiffness for each front and rear tire,
– wheelbase of the vehicle,
– steer angle.
Active yaw control strategies usually use a feedback controller to compute reference yaw moment from the difference of the measured yaw rate and desired yaw rate. This feedback controllers usually utilize sliding mode, linear quadratic regulation, model predictive control or robust control strategies [3]. In addition, the upper controller can also be feedforwarded by a map. Then the feedback controller compensates inaccuracies and disturbances or variation of the vehicle parameters. The presented control algorithm is based on feedback sliding mode controller without feedforward loop.
To sufficiently describe the vehicle dynamic state is except the vehicle yaw rate also a vehicle side slip angle estimation necessary. Otherwise, the vehicle drift with small yaw rate can occur without control algorithm determination of the vehicle instability. From this reason, active yaw control strategies with the vehicle side slip angle estimator to set the right controller boundaries are always used.
Fig. 3Structure of active yaw control system algorithm [4]
![Structure of active yaw control system algorithm [4]](https://static-01.extrica.com/articles/19943/19943-img3.jpg)
4. Simulations
Presented universal dynamic vehicle model with control algorithm is able to simulate a lot of various maneuvers and vehicle dynamic states. Through these simulations can be realize detailed analysis of the vehicle handling performance in various external conditions. Results of the models with and without active torque distribution can be compared and potential effects of the active yaw moment control usage by heavy commercial vehicle can be estimated.
4.1. Vehicle stabilization
The main task of the proposed system is to stabilize the vehicle at the limit situations and keep it controllable for the driver. Due to the appropriate drive torque distribution, the limits of the total lateral tire forces acting on the drive axle can be enhanced which help to keep the vehicle handling stability [5]. For demonstration of the enhanced vehicle handling performance a single lane change maneuver on the road with lower friction coefficient was chosen. The friction coefficient was set to 0.5 which corresponds to drive on the wet asphalt or concrete road. The initial velocity was 50 km/h and steering wheel angle amplitude was set to 200 degrees which is front wheels steer angle about 8 degrees. Steering wheel angle during simulation is shown in Fig. 4. Simulated were both variants – with and without active differential.
Fig. 4Steering wheel angle during single lane change maneuver
4.2. Regulation of understeering
The second simulation was focused on potential vehicle understeering compensation through active differential. Heavy commercial vehicles are supposed to operate reliably in big range of loading. The transported cargo but change the understeering behavior in many cases. Therefore, it would be beneficial for vehicle handling to regulate the vehicle understeering or oversteering behavior through active differential. To demonstrate this effect on simulated vehicle the steady state constant radius cornering maneuver was chosen with radius 50 m. Vehicle accelerated during 20 secs from initial velocity 20 km/h.
4.3. Results summary
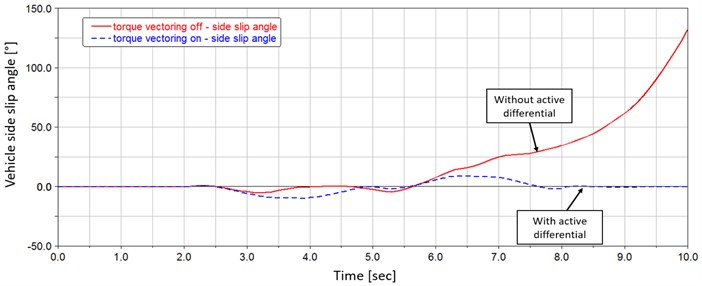
First maneuver represents transient behavior of the vehicle at the handling stability limits. Due to the active drive torque right-left distribution, the rear axle tire lateral force limit is enhanced, and the vehicle is during whole maneuver controllable. In Fig. 5 is the comparison of the resultant vehicle side slip angle during simulation. The red curve is side slip angle of the vehicle without active differential and the blue curve is vehicle with active drive torque distribution. It is obvious, that the vehicle without proposed system exceeded side slip angle limits and during 6th second of the simulation became unstable. Blue curve shows, that active differential is able to regulate effectively the side slip angle during transient dynamic state and keep the vehicle within the limits.
Fig. 5Vehicle side slip angle comparison during single lane change maneuver on wet road
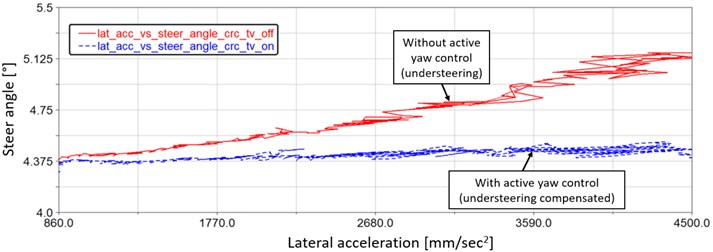
Second maneuver represents steady state vehicle dynamic behavior and demonstrates the possibility of the vehicle understeering regulation. The comparison of the vehicle with and without active right-left torque distribution system is in Fig. 6. This graph shows dependence of the steer angle and vehicle lateral acceleration. Red curve is the steer angle of the vehicle without active yaw moment control and it is obvious, that with increasing lateral acceleration, the driver has to increase the steering wheel angle too, to compensates the understeering. The blue curve shows, that by the vehicle with active differential, the tire longitudinal force difference on the drive axle is able to keep the vehicle to follow constant radius trajectory also at higher lateral acceleration.
Fig. 6Vehicle understeering comparison during steady state cornering
5. Conclusions
The presented method of the mechatronic system development shows potential of the active yaw moment control by heavy commercial vehicle. Due to the multibody model of the complete vehicle it is possible to predict dynamic behavior of complex system without building very expensive real prototype. Moreover, it is possible to verify function of the sophisticated control algorithm and analyzing the effects of the active differential. Results of the simulations show significant improvement of the vehicle handling performance according to the driver’s manipulating command during steady state cornering and transient dynamic states when limit is achieved. This improvement can play important role for vehicle maneuverability and active safety.
References
-
Piyabongkarn D., Lew Y. J., Rajamani R., Grogg J., Qinghui Y. On the use of torque-biasing systems for electronic stability control: limitations and possibilities. Transactions on Control Systems Technology, Vol. 15, Issue 3, 2007, p. 581-589.
-
Bauer F., Porteš P., Slimařík D., Čupera J., Fajman M. Observation of load transfer from fully mounted plough to tractor wheels by analysis of three point hitch forces during ploughing. Soil and Tillage Research, Vol. 172, 9, p. 69-78.
-
Novellis L. Wheel torque distribution criteria for electric vehicles with torque-vectoring differentials. Transactions on Vehicular Technology, Vol. 63, Issue 4, 2014, p. 1593-1602.
-
Rajamani R. Vehicle Dynamics and Control. Second Edition, Springer, New York, 2012.
-
Shibahata Y., Ahimada K., Tomari T. The improvement of vehicle maneuverability by direct yaw moment control. Proceedings of the First International Symposium on Advanced Vehicle Control (AVEC’92), Society of Automotive Engineers, Tokyo, 1992, p. 452-457.
About this article
The research leading to these results has received funding from the MEYS under National Sustainability Programme I (Project LO1202) and Specific Research Project of the Faculty of Mechanical Engineering, Brno University of Technology (FSI-S-17-4104).
