Abstract
In order to solve the problem that the inner surface of heterosexual surface parts is difficult to be machined, a solid-liquid two-phase abrasive flow machining method is proposed. The standard model and the pressure-coupled SIMPLEC algorithm are used. The dynamic characteristics of the dynamic pressure, turbulent kinetic energy and turbulence intensity of the polygonal spiral surface flow channel were obtained by numerical analysis of the solid-liquid two-phase abrasive grain polished polygonal spiral curved pipe under different outlet pressure conditions. The numerical simulation results show that the grinding effect is inversely proportional to the outlet pressure. We can achieve better polishing effect by appropriately reducing the outlet pressure.
1. Introduction
With the rapid development of science and technology, shaped surface parts have a wide range of applications in the aerospace, automobile manufacturing, mold manufacturing and other fields, such as: aircraft on the aviation impeller, gun guns in the helical surface, car turbocharger in the leaves, aspheric optical instruments, etc. [1, 2]. However, due to the complexity of the curved surface, especially for the surface quality requirements of high-profile curved surface, its ultra-precision machining is even more difficult; therefore, many scholars start a series of research work on a variety of surface processing technology [3-8]. Abrasive flow polishing technology can be used to realize ultra-precision finishing of various types of cavity surface and complex surface by virtue of its good profile modeling and flow characteristics [9].
2. Numerical simulation of solid- liquid two-phase abrasive flow numerical calculation of the initial conditions set
In this paper, the numerical simulation of the twelve-sided spiral curved tube is carried out. A three-dimensional single-precision steady state implicit solver is used to solve the problem by using the SMPLEC algorithm of pressure coupling equation in the Fluent. The turbulence model uses the standard - model, and the two-phase flow model uses the Mixture model. In the boundary condition, the inlet pressure of the solid-liquid two-phase abrasive grains is 8 MPa, and the solid phase is sic abrasive with the volume fraction of 0.2. The outlet boundary condition is pressure outlet, the values are 2 MPa, 3 MPa, 4 MPa, 5 MPa, the boundary condition is set to the non-slip wall boundary condition.
2.1. Numerical analysis and discussion of results
Simulation analysis was carried out at inlet pressure of 8Mpa and different pressure outlet conditions of 2 MPa, 3 MPa, 4 MPa and 5 MPa, to study the impact of export pressure on the polishing effect, in order to better analyze the flow field characteristics, take the axial section as the analysis surface, obtained the axial cross section dynamic pressure cloud diagram under different inlet pressure conditions is shown in Fig. 1.
Fig. 1Dynamic distribution of axial cross section under different outlet pressure

a) The outlet pressure is 2 MPa

b) The outlet pressure is 3 MPa

c) The outlet pressure is 4 MPa

d) The outlet pressure is 5 MPa
From the axial cross section dynamic pressure cloud diagram at different outlet pressures in Fig. 1, it can be seen that the dynamic pressure distribution is similar under different outlet pressure conditions, the dynamic pressure in the cavity along the flow direction is increasing and the moving pressure is smaller in the near wall, the dynamic pressure near the outlet is greater. With the gradual increase of the outlet pressure, the pressure difference between the inlet and the outlet decreases gradually, the turbulence of the fluid in the cavity decreases ceaselessly, and the impact and friction of the fluid on the wall are gradually reduced. Therefore, when the inlet pressure is constant, proper reduction of outlet pressure can improve the machining effect of abrasive flow.
The turbulent kinetic energy distribution of axial cross section under different inlet pressures of 2 MPa, 3 MPa, 4 MPa and 5 MPa is shown in Fig. 2.
Fig. 2Distribution of turbulent kinetic energy in axial cross section at different outlet pressures
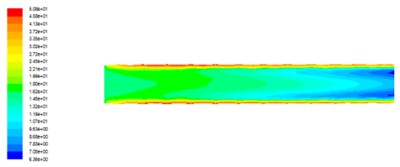
a) The outlet pressure is 2 MPa
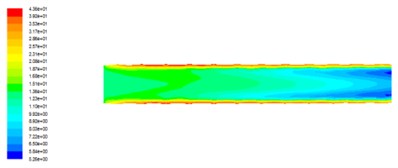
b) The outlet pressure is 3 MPa
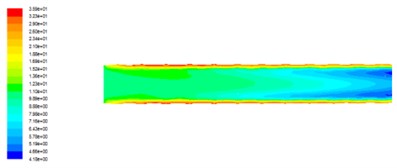
c) The outlet pressure is 4 MPa
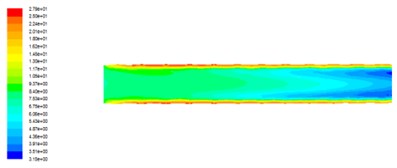
d) The outlet pressure is 5 MPa
It can be seen that the turbulent kinetic energy is smaller in the middle part of the flow channel, and the turbulent kinetic energy of the near wall is larger, and the turbulent energy is closer to the wall. The turbulent kinetic energy is larger, and turbulence can be gradually reduced in the flow direction. This is due to the abrasive flow motion in special-shaped surface cavity for free flow, when the abrasive grains collide with the edges of the polygonal spiral cavity, the fluid motion state suddenly changes, the velocity and the direction change suddenly in the vicinity of the wall. The variance of the fluid fluctuation will also increase, leading to the greater turbulent kinetic energy in the near wall region than in the middle of the runner, so, the abrasive flow polishing effect near the wall is better. With the increasing pressure of export, the pressure difference between inlet and outlet decreases, the turbulent kinetic energy decreases, and the turbulence in the runner is not sufficient. The ability of abrasive flow to glitch on the wall is also reduced.
Fig. 3Turbulent intensity distribution of axial cross section under different outlet pressures
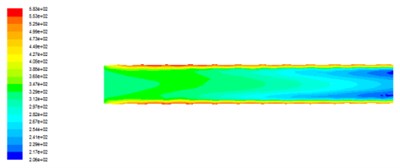
a) The outlet pressure is 2 MPa
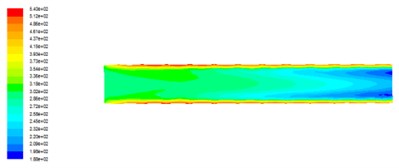
b) The outlet pressure is 3 MPa
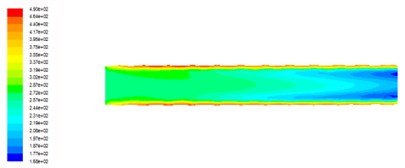
c) The outlet pressure is 4 MPa
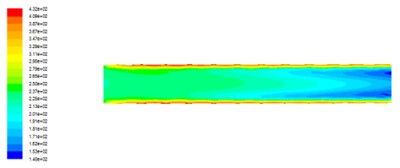
d) The outlet pressure is 5 MPa
It can be seen that the turbulence intensity is larger in the vicinity of the near wall and the turbulence intensity in the flow channel is smaller than that in the near-wall turbulence intensity, and the turbulence intensity decreases gradually along the direction of fluid flow. The turbulence intensity of the smaller areas is mainly concentrated in the exit. Comparison of Fig. 3(a)-(d) can be seen with the increase in outlet pressure, turbulence intensity became smaller. Because with the export pressure increases, the inlet and outlet pressure difference decreases, the turbulence intensity decreases, abrasive flow processing effect decreases.
3. Conclusions
In this paper, we propose a method of polishing the special-shaped curved surface with solid-liquid two-phase abrasive flow due to the complicated surface structure and difficult finishing of the surface of irregular curved surface parts. Through numerical analysis of polygonal spiral curved tube, it can be seen that the outlet pressure affects the polishing effect in the polishing of the special-shaped surface with solid-liquid two-phase abrasive flow. The outlet pressure increases, dynamic pressure, turbulence intensity, turbulent kinetic energy decreases near wall flow in multilateral spiral surface, the abrasive flow polishing effect is reduced. To achieve better polishing effect, the inlet pressure must be appropriate to reduce the outlet pressure.
References
-
Li Min, Yuan Julong, Wu Zhe, et al. Progress in ultra-precision machining methods for complex curved parts. Chinese Journal of Mechanical Engineering, Vol. 3, Issue 6, 2008, p. 144-147.
-
Li Junye Micro-Hole Abrasive Grain Polishing Device Development and Technology Research. Changchun University of Science and Technology, 2011.
-
Li Junye, Hu Jinglei, Qiao Zemin, et al. Technological parameter optimization and quality effects on solid-liquid phase abrasive flow polishing. Optics and Precision Engineering, Vol. 25, Issue 6, 2015, p. 1534-1546.
-
Li Junye, Xu Ying, Yang Lifeng, et al. Experimental and study on abrasive flow machining of non- linear tube parts. China Mechanical Engineering, Vol. 25, Issue 13, 2014, p. 1729-1734.
-
Ji Shiming, Qiu yi, Cai Yaojie, et al. Research on mechanism of ultrasound enhancing and the experiment based on softness abrasive flow. Journal of Mechanical Engineering, Vol. 50, Issue 7, 2014, p. 84-93.
-
Ji Shiming, Ma Baoli, Tan Dapeng Numerical analysis of soft abrasive flow in structured restraint flow passage. Optics and Precision Engineering, Vol. 19, Issue 9, 2011, p. 2092-2099.
-
Jishi Ming, Youzhi Fu, Tan Dapeng, et al. Study on dynamic characteristics of two-phase abrasive flow based on shear stress transport turbulent model. Acta Armamentarii, Vol. 33, Issue 4, 2015, p. 443-450.
-
Gao Hang, Wu Mingyu, Fu Youzhi, et al. Development of theory and technology in fluid abrasive finishing technology. Journal of Mechanical Engineering, Vol. 7, 2015, p. 174-187.
-
Bremerstein T, Potthoff A, Michaelis A, et al. Wear of abrasive media and its effect on abrasive flow machining results. Wear, Vols. 342-343, Issues 15, 2015, p. 44-51.
About this article
The authors would like to thank the National Natural Science Foundation of China No. NSFC 51206011, Jilin Province Science and Technology Development Program of Jilin Province No. 20160101270JC and No. 20170204064GX, Project of Education Department of Jilin Province No. 2016386.
