Abstract
In work, the questions of stabilization of factors of reliability of operation of the ship equipment are considered. According to the Navy Register rules, ship electrical power system voltage fluctuations within ±10 % of the nominal voltage are admissible if not lasting longer than 5 seconds; longer fluctuations are admissible if they are within ±5 % of the nominal voltage. The work of the engine with loads is presented. The algorithm for parameter optimization was applied. The calculation is performed on real parameters.
1. Introduction
When the dynamic characteristics of the ship propeller, the generator, the main engine (GD), or the rotation frequency regulator wear are changed, the free component of the main shaft rotational speed transient process is changed as well. If the ship is equipped with shaft generators (SG), such changes result in the fluctuations of the voltage they generate. Experimental studies identified [1] that the real transient process of ME rotational speed frequency changes is accompanied by large-amplitude fluctuations in exceed of 10 % and 5 seconds depending on the navigation conditions [2]. To increase the efficiency of fleet operation in the world, work is underway to introduce an automated fleet management system, to optimize its subsystems. The essence of optimal control lies in the criterion of optimality, which should be selected in the most generalized manner. At the level of ship power plants (SRS), the optimum criteria can be the minimum fuel consumption, the maximum efficiency of the plant or group of units, the minimum reversal time for the main engine and other partial criteria arising from the economic or technical objectives of the higher levels of the control system.
Increasing the efficiency of power plants is achieved in two ways: improvement of newly produced equipment in the direction of reducing specific fuel consumption, increasing reliability to reduce depreciation charges; rational operation of existing plants, which consists in selecting the most advantageous composition of the operating equipment, the most favorable load distribution between the operating units, carrying out repairs and cleansing at the optimum time, and operating individual units in the optimum mode.
2. Description of the object of the research
The ship power installation (PI) being investigated in operation consists of the main electric power source and the main power plant (MPP).
The main source of electricity in the system under investigation is the diesel generator sets DGA1, DGA2, ..., consisting of synchronous generators SG1, SG2, ... driven by diesel engines D1, D2, ... (Fig. 1).
The main power plant consists of main engine (DG), propelling the vessel with the help of variable pitch propeller (VPP). The shaft is articulated with the GD through an elastic coupling (EC) and gearbox (G). The speed of the vessel's movement is changed by turning the blades of the BPM by means of the step change mechanism (SCM). A shaft generator (VG), which is a power take-off generator, is connected to the reducer from which the shaft drive comes out.
Fig. 1Electromechanical system with power take-off from the main power plant
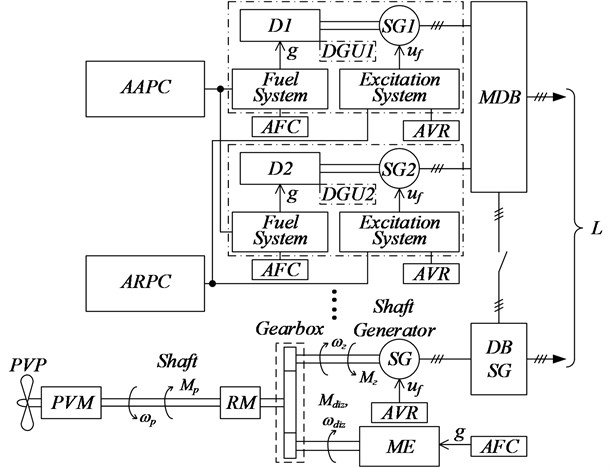
All generators are connected in parallel to common buses of the main distribution board (MDB). Receivers (R) receive electrical energy from the main switchboard and the MDB. Ship power system is limited in power.
All exciters are supplied with excitation voltage , and all diesel engines receive fuel with a flow rate of . For DGA, which is the leading group of parallel-running generators, automatic voltage regulation (AVR) and automatic frequency control (AFC) systems are used. For DGA, which are driven in a group of parallel-running generators, the active and reactive power is regulated using regulators, respectively, AAPC and ARPC, acting on the diesel through the fuel system, and on the generator through the excitation system.
Modern vessels, and therefore diesel installations on these vessels are operated in various seas and influenced by large number of factors that affect the moment of screw resistance. Such operating factors include: wear and roughness of the propeller, depth of the channel, draft of the ship, wind conditions, trawl resistance, ice conditions, seawater density, torsional oscillations of the propeller shaft [1, 2].
The transient process of changing the rotational speed of the shaft generator is influenced by the change in the torque of the diesel engine, the shaft generator and the screw, which follows from the main equation of the dynamics of the GD [3]:
where – the moment of diesel engine in normal conditions of operation; – the moment of resistance of the synchronous generator; – the moment developed by the screw.
The moment developed by a screw in water is determined by the formula [3-5]:
where – the dimensionless coefficient of torque, – the density of water, – the rotational speed of the screw, and is the diameter of the screw.
At a constant speed of the propeller of the adjustable pitch, the moment of resistance on the shaft of the main motor is equal to the sum of the moments of the resistance of the shaft generator and the screw. When changing the power of the adjustable pitch screw under the influence of operating factors, it is also necessary to change the power of the main motor to maintain a constant speed.
The change in the moment of the screw’s resistance, at constant revolutions, leads to the same power change. We attribute the change in the torque of the screw resistance to change in , a coefficient that depends on the relative flow and conditions of the vessel’s voyage.
Fig. 2Constructional diagram of the main power plant (MPP) and shafting: 1 – adjustable pitch screw (APC); 2 – the propeller shaft; 3 – mechanism for changing the pitch of the screw SCM; 4 – the basic bearings of sliding; 5 – flange connection; 6 – shaft generator; 7 – reducer; 8 – the main engine (DG); 9 – an intermediate shaft; 10 – a flywheel; 11 – flexible coupling
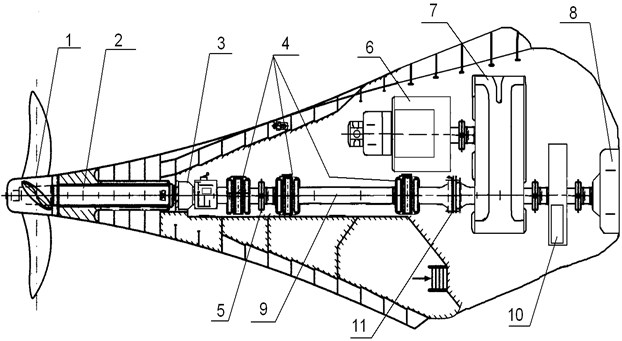
3. Solution of problem
The ME, it is impossible to identify the diesel and propeller parameters affecting the dynamic characteristics of the loaded ME under various conditions of ship navigation. Under such ME operating conditions, the dynamic characteristics of the rotational speed Automatic Control System (ACS) can be stabilized by adaptive controls this paper proposes, which are based on a sliding-mode regulator. For the operation of a rotational speed ACS with a sliding-mode regulator, there is no need to identify the diesel and propeller parameters; however, one needs a quantitative assessment of the limits within which such parameters could change. To implement the algorithm of such sliding-mode regulator, it is enough to control the rotational speed deviation for the specified value. The parallel operation of power plants (SPP) is widespread on ships of the sea and fishing fleets. When ship power plants operate in parallel: reliability of ship power plants and ship propulsion system increases; Improves the quality of electricity generation; More rationally uses the installed capacity and, consequently, increases the efficiency of the grid; the area occupied by the SPP is reduced due to the use of medium-speed main engines.
In connection with the wide spread of parallel operation of the SPP, the issues of increasing their economy, reducing fuel consumption are becoming increasingly important. The ME rotational speed ACS in the parallel operation of SG:
where:
, are the initial conditions; 428 rpm; 610,…, 678 kg·m2 is the total moment, the flywheel, the SG, the propeller shaft, the propeller.
, , , , , ; is the relative change; is the initial propeller pitch condition; is the equation taking into account the nature of propeller shaft resistance moment under storm conditions.
We calculated the partial derivatives for the time of the generator on the basis of a different type of signals. According to speed:
4. Practical calculation of model parameters of the algorithmic model
The questions of choosing the optimal composition of operating units, distribution of loads between them in the optimal way have found wide application in power engineering for optimization operation modes of power plant units, groups of power stations, power systems. This is due to the receipt of a significant economic effect due to the large power plant units and the wide use of automation and computer systems for the management stations and power systems.
The methods used to optimize the energy systems are very complex, most of them are based on the condition of equality relative increments in fuel consumption, which is only a necessary condition for the existence of an extremum. To account for restrictions, the method of penalty functions is applied, which allows for the possibility of computing. Methods of dynamic programming, branches and boundaries are also quite complex and require the use of digital computers. The complexity of developing a criterion for the optimal load distribution between aggregates and the choice of the optimal composition of operating aggregates consists in finding the extremum of the function with nonlinear dependencies, constraints of the form equalities and inequalities, and the discrete part of the problem of choosing the optimal composition of operating aggregates, which excludes the possibility of using the classical apparatus for finding the extremum [3-7].
Initial model parameters (universal characteristics of an 8NVD48A2U ship diesel near the point with 350 rpm).
Derive the formula for calculating the partial derivative position [4-8].
We calculate the partial derivative for four points of the universal characteristic [5-8]. The position of the fuel pump rail does not change. The calculated points are chosen on the line of unchanged power. 26 %, 42 rad/s, 24 %, 44.6 rad/s, 92 %, 42 rad/s, 88 %, 44,6 rad/s.
The minimum value of the partial derivative with 1.04:
The maximum value of the partial derivative at 0.8:
The partial torque derivative of the 8NVD48A2U diesel engine varies according to the speed: –358,..., –132
5. Conclusions
Fouling, corrosion of the propeller, weather conditions of the ship's sailing change its moment of resistance. The free component of the transient process of changing the voltage frequency of the generator in the transient processes changes. There is an angle between the EMF of the generator and the EMF of the diesel generator of the ship power station operating in parallel. This leads to the occurrence of equalizing currents between them. It has been analytically proved that in the storm conditions of the ship's navigation, the shaft generator falls out of synchronism due to fluctuations in the rotational speed of the crankshaft of the main power plant.
References
-
Rutkowska D., Pilinsky M., Rutkowski L. Neural Networks, Genetic Algorithms and Fuzzy Systems. Hotline Telecom, 2004.
-
Zhilenkov A., Chernyi S. Investigation performance of marine equipment with specialized information technology. Procedia Engineering, Vol. 100, 2015, p. 1247-1252.
-
Chernyi S., Zhilenkov A. Modeling of complex structures for the ship’s power complex using XILINX system. Transport and Telecommunication, Vol. 16, Issue 1, 2015, p. 73-82.
-
Nyrkov A., Sokolov S., Zhilenkov A., Chernyi S. Complex modeling of power fluctuations stabilization digital control system for parallel operation of gas-diesel generators. IEEE NW Russia Young Researchers in Electrical and Electronic Engineering Conference, Saint Petersburg, Russia, 2016, p. 636-640.
-
Malioutov D., Corum A. Cetin M. Covariance matrix estimation for interest-rate risk modeling via smooth and monotone regularization. IEEE Journal of Selected Topics in Signal Processing, Vol. 10, Issue 6, 2016, p. 1006-1014.
-
Chaudhuri A., Stenger H. Survey Sampling Theory and Methods. Chapman and Hall, New York, 2005, p. 416.
-
Nyrkov A., Chernyi S., Zhilenkov A., Sokolov S. The use of fuzzy neural structures to increase the reliability of drilling platforms. Proceedings of the 26th International DAAAM Symposium, 2016, p. 0672-0677.
