Abstract
In order to protect the ship’ s magnetic field information from detection, a method is proposed to camouflage both the amplitude and curve of ship’s magnetic field based on multi-objective genetic algorithm. The example shows that the method can camouflage the ship’s magnetic amplitude and curve feature effectively, the multi-objective genetic algorithm can avoid the subjective of weight distribution in the unified objective method and the alternative Pareto disaggregation can be found, which is more adaptable for application requirement.
1. Introduction
The ship’s magnetic field is the stable signal source of underwater martine magnetic weapons, the magnetic field features can be obtained after analysis of a large number of magnetic field data, which can be used as the accurate technologic reference (such as sensitivity) for designing and operating magnetic weapon, or to establish the date base for surveillance and identification [1-3]. To protect magnetic field form being detected, in this paper, the multi- objective genetic algorithm was used to calculate and adjust the degaussing coil’s currents to control magnetic amplitude and the features of curve into a camouflage condition. The multi-objective genetic algorithm can avoid the subjective of weight distribution in the uniform objective method. And also, the alternative Pareto disaggregation can be found, which is more adaptable for application requirement.
2. Mathematical model of ship’s magnetic field camouflage
Degaussing system decrease the ship magnetic field by the opposite magnetic field generated by degaussing coils’ current. The adjustment of degaussing coils equals that each coil is correctly distributed current to minimize the error between the magnetic field of ship and that generated by all the coil together [4]. Thus, the ship culminates in terms of degaussing. 41 observation points are chosen,which are evenly distributed within the twice of the ship length range under the keel at the standard measure depth, after degaussing system is on, the vertical magnetic field of the ship is and its amplitude is . when degaussing system is off, the ship’s vertical magnetic field is and its amplitude is . Because the distinction of magnetic field amplitude and magnetic field curve is closely related to the performance of magnetic weapons, the camouflage is mainly focused on the magnetic amplitude and curve. After the camouflage, the vertical magnetic field is and the amplitude is . In order to keep the diversity of camouflage, it can preset various camouflage magnetic field amplitude based on the requirements, and the should be larger than ,and less than . The camouflaged objectives are
1) Minimize the absolute error between and :
2) Maximize the average error between the normalized magnetic field absolute value of and :
The equation above can be transferred into founding the minimum:
In the equation, is the serial number of the observation points and 41 is the total number of the points.
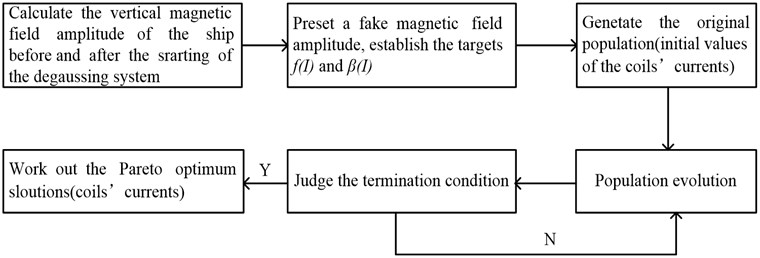
When it is to solve the multi-objectives optimization, it is more simple to sum up all the objectives into a uniform objective by weight distribution,while the weight is susceptible to subjectivity. The multi-objective genetic algorithm connects the Pareto domination theory in economics and the genetic algorithm, which can find out the Pareto disaggregation, so it is more pragmatic. As follows is the calculation steps of the multi-objective optimization function gamultiobj in MATLAB and improved based on NSGA-II [5].
• Make sure the constraint type;
• Generate the original population;
• Population revolution: choice, crossover, mutation, generation of sub-population, combination of original population and sub-population, calculation of rank and distance, non-dominated rank, calculate of crowding distance, trim population, calculate of average distance and spread;
• Plot the first front;
Judge the termination condition:
If satisfied, the Pareto optimum result comes out;
If not satisfied, the population revolution goes on.
The calculation steps of the coils’ currents by function gamultiobj in the process of ship magnetic field camouflage is illustrated in Fig. 1.
Fig. 1Calculation steps of the coils’ currents in the process of camouflage
3. Case study
3.1. Main experiment and calculation parameters
Fig. 2 shows three kinds of ships’ degaussing coils: longitudinal coil (L coil), athwartship coil (A coil) and vertical coil (V coil) [6-8].
In this paper, the ship model is equipped with a total of 31 sets of coils. The coils’ currents range is –5 A-5 A, which the degaussing supply supplies. The magnetic field of individual coil is measured by three components magnetic sensor in the laboratory, the observation points are evenly distributed within the twice of the ship length range under the keel at the standard measure depth, then the magnetic value could be calculated when the coil current is 1 A, which is called as coil’s efficiency. The typical vertical, athwartship and vertical coil’s normalized efficiency is shown in Fig. 3, in which the normalized efficiency is the ratio of each coil efficiency to the maximal value of all the three coils efficiency.
The main parameters of gamultiobj as shown in Table 1.
Fig. 2Schematic of degaussing coils: a) L coils; b) A coils, c) V coils, d) Assembly coils
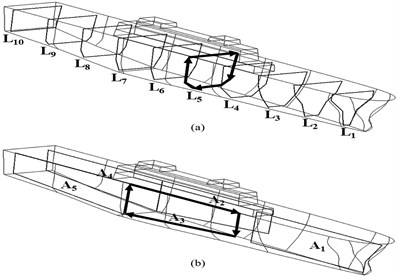
Fig. 3Typical normalized coils’ efficiency
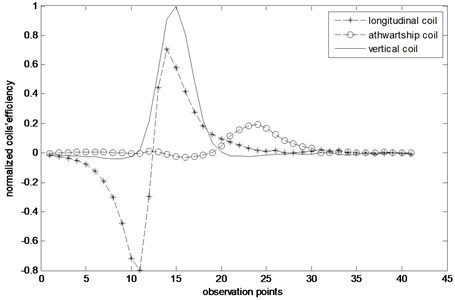
Table 1The main parameters of the algorithm
Algorithm parameters | Value |
Pareto Fraction | 0.1 |
Population Size | 400 |
Generations | 200 |
Stall Gen Limit | 200 |
3.2. Results analysis
During a camouflage process, preset calculation result in this camouflage mode as shown in Fig. 4.
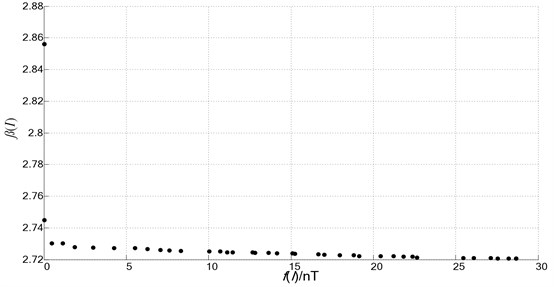
It is observed from Fig 4 that the multi-objective genetic algorithm can find the Pareto solutions within the specified maximum number of iterations, the distribution of in the solutions is wide (between 0-30 nT) but smaller magnitude, Which indicates that the amplitude of the magnetic field of the ship is close to the preset false magnetic field amplitude; the distribution of is relatively concentrated, and the change of of is no longer obvious when is greater than 20 nT.
Fig. 4Pareto front distribution
Multi-objective genetic algorithm can obtain alternative solutions, which can be selected according to the actual application. For the purpose of camouflage, it has been able to effectively achieve magnetic field amplitude camouflage, when the absolute error between the amplitude of the ship’s magnetic field and the preset false amplitude is less than 10 nT. Therefore, the final solution of the magnetic field camouflage can be chosen according to the following steps: first of all, choose solutions when the less than 10 nT, and then choose the solution when is smallest, and use the coils’ currents corresponding to the
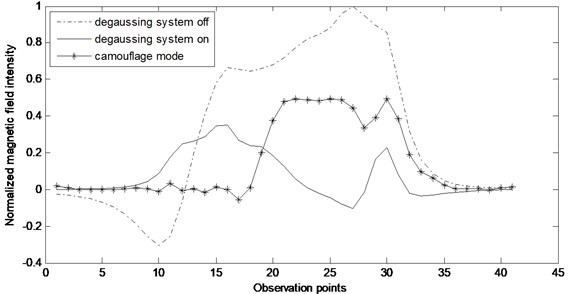
final solution to calculate the ship magnetic field in the camouflage mode. From Fig. 5, It can be seen that the amplitude of the magnetic field can be controlled well at a preset false level in the camouflage mode, and between the amplitudes of the ship magnetic field before and after the degaussing system is turned on; when camouflaged, the magnetic field curve changes obviously compared with degaussing system opened.
Fig. 5Normalized magnetic field intensity under the keel
4. Conclusions
By controlling the coils’ currents of the onboard degaussing system, an effective camouflage of the magnetic field amplitude and the curve characteristics of the ship is realized. The multi-objective genetic algorithm can avoid the subjectivity of the weight assignment in the unified objective method, which can obtain alternative solutions, and the solutions are more in line with the actual demand.
References
-
Wang Hai-yun, Dong Da-qun Application of ship’ magnetic field model parameters to recognizing target. Ship Engineering, Vol. 5, Issue 3, 1999, p. 46-49, (in Chinese).
-
Wen Wu-di, Liu Zhong-le, Li Hua Ship classifying method based on vectorial magnetic field of warship. Mine Warfare and Ship Self-Defense, Vol. 21, Issue 3, 2013, p. 42-45, (in Chinese).
-
Jong D. A., Cococcioni M. Fuzzy logic generic mine model. Conference Proceedings of Undersea Defence Technology, NATO, Berlin, 2007.
-
Zhu Xian-qiao, Liu Da-ming, Yang Ming-ming Degaussing coils optimal calibration method based on multi-objectives. Journal of Beijing University of Aeronautics and Astronautics, Vol. 38, Issue 11, 2012, p. 1507-1511, (in Chinese).
-
Shi Feng, Wang Hui, Yu Lei, et al. MATLAB Intelligent Algorithm 30 Cases Studies. Beihang University Press, Beijing, 2011.
-
Choi N., Jeung G., Yang C., Chung H., et al. Optimization of degaussing coil currents for magnetic silencing of a ship taking the ferromagnetic hull effect into account. IEEE Transactions on Applied Superconductivity, Vol. 22, Issue 3, 2012, p. 4904504.
-
Choi N., Jeung G., Jung S., Yang C., Chung H., et al. Efficient methodology for optimizing degaussing coil currents in ships utilizing magnetomotive force sensitivity information. IEEE Transactions on Magnetics, Vol. 48, Issue 2, 2012, p. 419.
-
Giwoo Jeung, Nak-Sun Choi, Chang-Seob Yang, et al. Indirect fault detection method for an onboard degaussing coil system exploiting underwater magnetic signals. Journal of Magnetics, Vol. 19, Issue 1, 2014, p. 72-77.
