Abstract
A new approach based on Gauss-Newton iteration is proposed to estimate modal damping. Noise resistance of the proposed method and half-power bandwidth method are analyzed and compared by plenty of simulations with different signal-to-noise ratios (SNR). The proposed method is more accurate and stable than half-power bandwidth method in all SNRs, especially when the noise level is high. If ≤ 30 dB, the proposed method should be used for damping estimation instead of half-power bandwidth method. A damping estimation experiment is carried out with both methods, and the results indicate and verify that there is smaller variability for the proposed method.
1. Introduction
Since damping is a valuable parameter for resonant response of structures or systems, damping is of great significance for structural dynamics. It is difficult to obtain damping through a theoretical method so that the universal way for damping estimates is experimental investigation [1, 2]. Half-power bandwidth method [3, 4], which calculates resonant damping with frequency bandwidth for vibration energy decreases 3dB and the resonant frequency, is a widely used approach for damping estimation. Half-power bandwidth method is introduced as main method for damping estimates in the American test standard ASTM E756-05. Bertha [5] obtained damping of a system that does not possess real modes with half-power bandwidth method. Guo [6] improved the half-power bandwidth method and proposed a new method based on integral opinion. Badsar [7] determined the material damping ratio in shallow soil layers with the half-power bandwidth method.
As the half-power bandwidth method uses only three data points, its accuracy will be affected by the signal-to-noise ratio (SNR). When some of the three data points are seriously affected by noise, a large error will appear and cannot be neglected. The aim of this work is to put forward a new method which has high accuracy and strong noise resistance by using the amplitude of frequency response.
2. Half-power bandwidth method
A widely used method, namely half-power bandwidth method, is introduced as follows. The damping loss factor can be obtained by the quotient of half-power bandwidth and the resonant frequency, as shown in Eq. (1):
The diagrammatic sketch of the method is shown in Fig. 1.
The half-power bandwidth method is a classical and widely used method, but there is a fatal short coming that if the signal-to-noise ratio (SNR) is not high enough. It is difficult to recognize the half-power bandwidth, seen in Fig. 2.
It can be seen in Fig. 2 that the half-power bandwidth is hard to decide because there are more than two frequencies related to half-power response.
Fig. 1Half-power bandwidth method
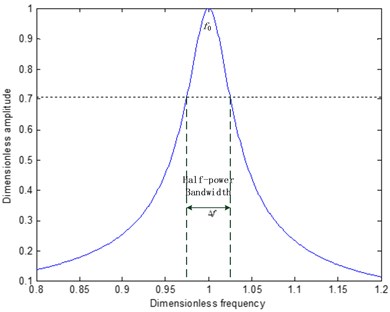
Fig. 2Half-power bandwidth method with low SNR
3. Damping estimation based on Gauss-Newton iteration
The parameter of damping is often estimated with data near the resonant frequency. The widely used half-power bandwidth method for damping investigation only uses three data points of frequency response so that it will cause a large error when the experimental data is affected by noise. It is expected to obtain a more accurate damping if more data points of frequency function are used. Therefore, a new approach based on Gauss-Newton iteration is proposed in which a numbers of data points near resonant frequency are used.
The amplitude of frequency function is:
where is excitation force, the stiffness, natural circle frequency, and the loss factor.
It is obvious that the maximum amplitude can be obtained:
The dimensionless amplitude is defined as:
Rewrite Eq. (4) as:
where:
is dimensionless parameters and represent placement.
A number of data points (1, 2,…, ) can be obtained according to the experimental frequency response. The residual error is defined as:
The damping identification can be transferred into getting a proper value of to make the residual error the most minimum. Gauss-Newton iterative method is used to find the optimal parameter of damping.
Expand Eq. (5) to Taylor series at point of initial value as:
where .
Rewrite Eq. (7) as:
where ,. Eq. (9) is a typical least square optimization problem. The estimated can be obtained for the first generation by solving Eq. (10):
where , .
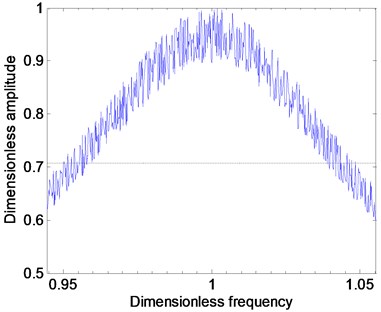
After is obtained, will be replaced by and repeat the above step to get the estimated value for the second generation. The iteration will be finished if the difference between the neighbor generations of is small enough for satisfactory demand. The last generation of is the estimated damping. The experimental and fitting response are shown in Fig. 3 and damping can be obtained in the fitting process.
Fig. 3Experimental and fitting response
4. Resistance to noise
This simulation is conducted to illustrate the noise sensitivity of the proposed methods. A single-degree-of-freedom system is adopted to verify the validity of Gauss-Newton iteration. A comparison is made between the proposed method and half-power bandwidth method. Gaussian random noise is applied to the simulated frequency response, and the signal-to-noise ratio (SNR) is defined as:
where is amplitude of effective signal and is amplitude of noise.
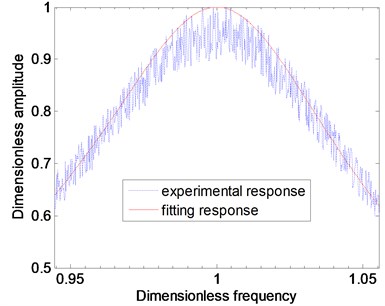
The simulated signal parameters are 0.001, 500 Hz, , and 0.1 Hz. It is simulated on 1000 samples with the SNR in the range from 10 dB to 50 dB. Errors of estimated damping with the two methods are shown in Fig. 4.
In Fig. 5, each method is tested for 41 noise levels, which is from 10 dB to 50 dB with 1 dB interval, with 1000 samples in each noise level. The average error is calculated by Eq. (12):
where is the identified damping, is the exact loss factor set in the simulation, is the number of samples.
Fig. 4Error of the estimated damping versus SNR: a) proposed method, b) half-power bandwidth method
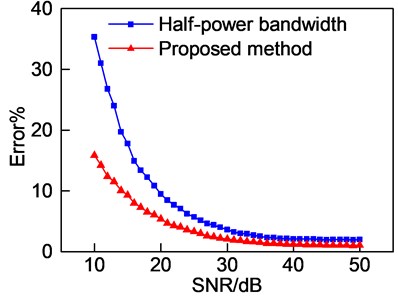
Fig. 5Average error for the two methods
It can be seen in Fig. 4 that identified damping by the two methods are more and more accurate with the increased SNR. The accuracy of proposed method is more than half-power bandwidth method at all SNRs. It may also be noticed that there is considerable variability of half-power bandwidth method especially in the lower SNR.
As seen in Fig. 5, both methods are of satisfied accuracy if 30 dB. But if 30 dB, error of half-power bandwidth is much larger than proposed method. It is clear that the proposed method should be used to estimate damping instead of half-power bandwidth if 30 dB.
5. Conclusions
A novel method based on Gauss-Newton iteration is proposed to estimate damping in this paper. There is smaller variability for the proposed method than half-power bandwidth method. The proposed method is more accurate than half-power bandwidth method, especially in the lower SNR circumstances. The proposed method should be used instead of half-power bandwidth method for damping estimation if 30 dB.
References
-
Guasch Oriol A direct transmissibility formulation for experimental statistical energy analysis with no input power measurements. Journal of Sound and Vibration, Vol. 330, 2011, p. 6223-6236.
-
Rak Michal, Ichchou Mohamed, Holnicki Szulc Jan Identification of structural loss factor from spatially distributed measurements on beams with visoelastic layer. Journal of Sound and Vibration, Vol. 310, 2008, p. 801-811.
-
Papagiannopoulos George A., Hatzigeorgiou George D. On the use of the half-power bandwidth method to estimate damping in building structures. Soil Dynamics and Earthquake Engineering, Vol. 31, Issue 7, 2011, p. 1075-1079.
-
Wang P. W., Zhong W. W., Hsu J. F. Investigation of multi-layer sandwich beams through single degree-of-freedom transformation. Applied Acoustics, Vol. 74, Issue 4, 2013, p. 521-525.
-
Olmos Bertha A., Roesset Jose M. Evaluation of the half-power bandwidth method to estimate damping in systems without real modes. Earthquake Engineering and Structural Dynamics. Vol. 39, 14, p. 1671-1686.
-
Guo Zhiwei, Sheng Meiping, Ma Jiangang, Zhang Wulin Damping identification in frequency domain using integral method. Journal of Sound and Vibration, Vol. 338, 2015, p. 237-249.
-
Badsar S. A., Schevenels M., Haegeman W., Degrande G. Determination of the material damping ratio in the soil from SASW tests using the half-power bandwidth method. Geophysical Journal International, Vol. 182, Issue 3, 2010, p. 1493-1508.
