Abstract
To our knowledge, iterative learning control (ILC) is an effective method for active vibration control of mechanical systems with periodically varying parameters, merits of ILC mainly include simplicity and completely compensating for nonlinear. However, during application of ILC, transient growth or instability for system is sometimes dramatic large which is in fact detrimental to system, we attribute such phenomena to non-periodic factors, so, an improvement to iterative learning control (ILC), predictive gain iterative learning control (PILC) is put forward to suppress the rotor displacement and the amplifier current mainly resulted from the unbalance forces. Discretization is applied to get the system model including the parameters analysis, and then, the obtained model is transformed into a new style where the learning gain is input, next, based on the new model, a feedback predictive control algorithm is carried out to obtain the learning gain at present time, then, at the next time, the gain is updated by the same mean. The improved method achieves arbitrary damping and gets a high speed and accuracy output tracking for mechanical system. The simulation results show that the control technique can reduce transient growth and can significantly increase the stability of the rotor system.
1. Introduction
In the rotating machinery, rotor mass grievances is difficult to avoid even if very high precision rotor, the centrifugal force of the rotor is proportional to the square of the speed, hence, even very small eccentricity will have a great centrifugal force in high speed rotating machinery, then result in unbalanced vibration, furthermore, because the rotor mass imbalance can cause the same frequency and speed exciting force when the rotational speed reaches a certain level, the amplitude unbalance vibration will be more than gas gap, consequently, rotor friction happen and make the system out of control, seriously affected the dynamics performance and safe operation. In addition, the rotary motion error of the rotor is also one of the key factors for high-precision machinery. Thus, the rotor vibration control becomes more and more important.
A number of techniques for active rotor vibration control have been demonstrated successfully in the literature [1-19], these include linear quadratic Gaussian (LQG) [7], mode separation method [8], finite element method (FEM) [9, 12, 14, 15,], Lure-type Lyapunov function [10], Lagrange approach [11], induction machine[13], additional artificial damping[16], implicit Runge-Kutta method [17], the Monte Carlo method [18],vibration mechanism [19], however, some of the methods are rarely used in practice because of their implementation complexity [21].
In [20] learning control is developed to suppress rotor vibration. This skill can easily be implemented without additional measurements and without modification of existing feedback/feedforward controller [20], the chief advantages of ILC are the simplicity of the controller, excellent property, and guaranteed stability [20], and what is worth mentioning is that ILC is identified as the most effective means to suppress periodic vibration, so making use of ILC to eliminate of the forced vibration of magnetically suspend rotor is to the point. However, the learning control is often low-pass filtered with a Q-filter to prevent transient growth at the cost of performance [21].
In this work, an improvement to ILC is described which gets a variable learning gain by predictive method. On the premise that algorithm is convergence and system is stability, the modified dramatically reduces the transient vibrations, what’s more, it takes a shorter time to reach tracking error requirement, and gets a smaller tracking error in the same time period in contrast to others ILC Algorithm.
2. Problem description
2.1. System structure
Although the technique of iterative learning is applicable to a wide range of mechatronic system, in this work, the proposed controller is applied to a rotor with magnetic bearings pictured in Fig. 1 [22].
Fig. 1The rotor-shaft model
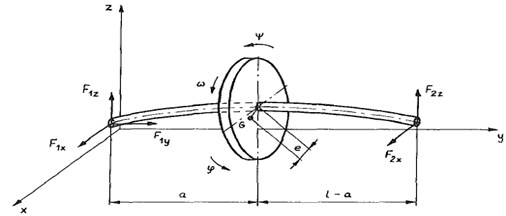
It can be seen from Fig. 1 that a slightly unbalanced disc of mass is mounted to a massless flexible shaft which is nonsymmetric cross-section and suspended by two magnetic bearnings, several electromagnets are arranged around the shaft. The position of the shaft is constantly monitored by noncontacting sensors, the measuring signals are processed in a controller, fed back as a control current to the coils of electromagnets which attract or repel the shaft [20].
2.2. Model of system
In order to get the model equation, some definitions as following: is the eccentricity of disc, system constant angular velocity is, , , denote the disc displacements of the center along , , axes respectively and , are rotations in the plane and plane of disc apart, then the inertia forces and moments of the disc are [20]:
the dynamic equations of the disc are:
where , are the moments of inertia of the disc with respect to its axis and to diameter, respectively, , are the components of the dynamical forces in the bearings in and direction apart, denotes the distance between the bearings and is the distance of the disc to the bearing.
Now, taking axis for example, assuming both magnetic bearing are identical, we get:
where , denote the position stiffness and the current stiffness of the bearings respective, is a time variant coefficient, satisfying:
where , are the principal moments of the shaft cross-section, is Young modulus of the shaft material, from Eqs. (5), (9)-(11), we have:
2.3. Control task
In Eq. (13), the system input , is the system output, is a influence coefficient which varies periodically in time. The control task is to design a controller to eliminate the rotor vibration caused by unknown unbalance, the feedback control gains selected are such that obtain the damping ratio and the steady-state error for the closed loop system are equal to 0.707 and 10-4, the desired output is equal to zero [20].
3. Controller design
Iterative learning control has been one of the best methods for the rotor vibration control, there are a set of example for learning rule, for simplicity and not loss generality, we consider learning law given by:
where is the learning gain, and next, a predictive control method is utilized to decide the value of .
Firstly, we write Eq. (13) in a state-space representation:
Eq. (16) can be written in matrix form:
where:
then, we get the dispersed equation of Eq. (17):
and is sample period, the system state space is:
where , at in the time index and 1 in the iterative index, inserting Eq. (13) into Eq. (19), we have:
defining that the predictive model is
In order to overcome the effects on predictive value of the model owe to disturbances and model excuse factors, the difference between the calculated value and the measured value of model is used to amend the predictive gain:
Reference trajectory is described as:
The objective function for optimization control can be express by:
Finally, according to least squares, we gain the best value:
4. Simulation
In this section, the simulation are performed .The numerical data were as following: 10 kg, 6 N/mm, 0.5 mm, 0.01 nn/N, 10 N/mm, 0.3, 628 rad/sec, 0.003 sec.
Fig. 2System output of the 3th iterative
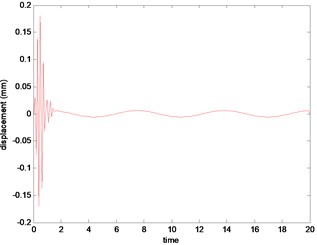
Fig. 3System output of the 7th iterative
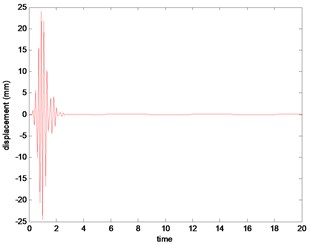
Figs. 2, 3 are the displacement outputs of the disc center in direction in a period without predictive gain, what can be learned from which is that the instantaneous vibration bandwidth become more and more big with the increase of the number of iterations.
Figs. 4-5 are system outputs with the time-dependent predictive gain. The predictive gain iterative learning controller is superior to the class learning gain, in the simulation process, the predictive steps is two steps predictive, multistep can get the better control result, but the calculation burden greatly increases.
Aiming at getting a more intuitive understanding for the advantage of the scheme proposed by this paper, Figs. 6-7 are given.
Fig. 4System output of the 5th iterative
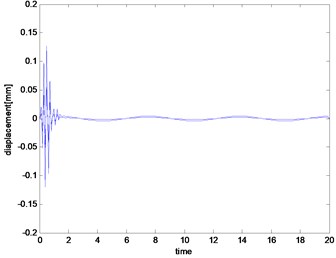
Fig. 5System output of the 11th iterative
Fig. 6Error output in the iterative index
Fig. 7Comparison between predictive gain and fixed gain
5. Conclusions
In this study, a gain predictive algorithms is added to a learning controller, the resulting learning gain changes with time which greatly improves the ideal trajectory tracking rate and reduces the steady state error.
In addition to open loop iterative control, the predictive variable gain can also be applied to other learning controller. This allows the learning controller to be an exceptionally high performance tracking controller without sacrificing stability margins [23].
Simulations on a rotor model demonstrate the effectiveness of the proposed predictive gain learning controller.
Future work involves the research on the prediction steps and application to coupling nonlinear system.
References
-
Fan J., Zhencai Z., Wei L., Gongbo Zh., Guoan C. Fault diagnosis of rotating machinery based on noise reduction using empirical mode decomposition and singular value decomposition. Journal of Vibroengineering, Vol. 17, Issue 1, 2015, p. 164-174.
-
Ming L., Cheng L., Xianbo L., Hongguang L., Fucai L., Guang M. Nonlinear rotor dynamics on turbo expander with unbalanced bearing force caused by temperature difference. Journal of Vibroengineering, Vol. 17, Issue 1, 2015, p. 33-46.
-
Mingyue Y., Feng T. Characteristic analysis on the rubbing of rotor blade-casing of aero-engine based on Hilbert transform. Journal of Vibroengineering, Vol. 17, Issue 2, 2015, p. 733-742.
-
Yongsheng R., Yuhuan Z., Qiyi D., Xingqi Z. Primary resonance of a rotating composite shaft with geometrical nonlineary. Journal of Vibroengineering, Vol. 17, Issue 4, 2015, p. 1694-1706.
-
Liangliang Chen., Changsheng Z., Meng W., Kejian J. Vibration control for active magnetic bearing high-speed flywheel rotor system with modal separation and velocity estimation strategy. Journal of Vibroengineering, Vol. 17, Issue 2, 2015, p. 757-775.
-
Taskin Y. Improving pitch and yaw motion control of twin rotor MIMO system. Journal of Vibroengineering, Vol. 16, Issue 4, 2014, p. 1650-1660.
-
Enqiong T., Jiancheng F., Shiqiang Z., Dikai J. Active vibration control of the flexible rotor to pass the first bending critical speed in high energy density magnetically suspended motor. Journal of Engineering for Gas Turbines and Power, Vol. 137, Issue 11, 2015, p. 112-118.
-
Enqiong T., Jiancheng F., Bangcheng H. Active vibration control of the flexible rotor in high energy density magnetically suspended motor with mode separation method. Journal of Engineering for Gas Turbines and Power, Vol. 137, Issue 8, 2015, p. 503-510.
-
Ariasmontiel M., Silvanavarro G., Antoniogarcía A. Active vibration control in a rotor system by an active suspension with linear actuators. Journal of Applied Research and Technology, Vol. 12, Issue 5, 2014, p. 898-907.
-
Chamroon C., Cole T., Wongratan T. An active vibration control strategy to prevent nonlinearly coupled rotor-stator whirl responses in multimode rotor-dynamic systems control systems technology. IEEE Transactions on Control Systems Technology, Vol. 22, Issue 3, 2014, p. 1122-1129.
-
Staino A., Basu B. Dynamics and control of vibrations in wind turbines with variable rotor speed. Engineering Structures, Vol. 56, Issue 4, 2013, p. 58-67.
-
As D., Jk D. A reduced rotor model using modified SEREP approach for vibration control of rotors. Mechanical Systems and Signal Processing, Vol. 26, Issue 3, 2012, p. 167-180.
-
Sinervo A., Jokela T., Arkkio A. Controlling rotor vibrations of a two-pole induction machine with unipolar actuator magnetics. IEEE Transactions on Magnetics, Vol. 48, Issue 7, 2012, p. 2205-2210.
-
Chao L., Dongxiang J., Fulei C. Influence of alternating loads on nonlinear vibration characteristics of cracked blade in rotor system. Journal of Sound and Vibration, Vol. 353, Issue 8, 2015, p. 205-219.
-
Bang X., Shiyu W., Yaoyao W., Zhifu Z., Jie X. Magnetically induced rotor vibration in dual-stator permanent magnet motors. Journal of Sound and Vibration, Vol. 347, Issue 5, 2015, p. 184-199.
-
Jerzy S., Zbigniew K. Stability of a cracked rotor subjected to parametric excitation. Journal of Engineering for Gas Turbines and Power, Vol. 137, Issue 5, 2015, p. 508-516.
-
Jianming C., Paulallaire L., Timothy D. Coupled lateral and torsional nonlinear transient rotor-bearing system analysis with applications. Journal of Dynamic Systems, Measurement, and Control, Vol. 137, Issue 9, 2015, p. 11-20.
-
Chun-biao G., Yue-hua W., Shi-xi Y., Yan-long C. Nonparametric modeling and vibration analysis of uncertain Jeffcott rotor with disc offset. International Journal of Mechanical Sciences, Vol. 78, Issue 6, 2014, p. 126-134.
-
Qiuxiao W., Fei W. A new vibration mechanism of balancing machine for satellite-borne spinning rotors. Chinese Journal of Aeronautics, Vol. 27, Issue 5, 2014, p. 1318-1326.
-
Hac A., Tomizuka M. Application of learning control to active damping of forced vibration for periodically time variant systems. Journal of Vibration and Acoustics, Vol. 112, Issue 10, 1990, p. 489-496.
-
Douglas B., Andrew A. Monotonic convergence of iterative learning control for uncertain system using a time-varying filter. IEEE Transactions on Automatic Control, Vol. 53, Issue 2, 2008, p. 582-585.
-
Andrew F., Kam L. Integrated strain and force feedback for high-performance control of piezoelectric actuators. Sensors and Actuators, Vol. 161, Issue 4, 2010, p. 256-265.
-
Andrew F. Nanopositioning system with force feedback high-performance tracking and vibration control. IEEE Transactions on Mechatronics, Vol. 15, Issue 3, 2010, p. 433-447.
About this article
This research was supported by the Central Universities Funds (9160215006).
