Abstract
Detection of multiple damage using modal curvature in noisy environments has become a research focus of considerable challenge and great significance over the last few years. However, a noticeable deficiency of modal curvature is its susceptibility to noise, which usually results in a noisy modal curvature with obscured damage signature. To address this deficiency, this study formulates a new concept of complex-wavelet modal curvature. Complex-wavelet modal curvature features the ability to reveal and delineate damage under noisy conditions. The effectiveness of the concept is experimentally validated in a carbon-fiber-reinforced polymer composite beam with three cracks, for which mode shapes are measured by a scanning laser vibrometer. The experimental results show that the complex-wavelet modal curvature is capable of revealing slight damage by eliminating noise interference, with no need for prior knowledge of either material properties or boundary conditions of the beam under inspection.
1. Introduction
Vibration-based structural damage detection has been widely investigated in the mechanical, aerospace, civil, and infrastructure fields [1-4]. Furthermore, the identification of multiple damage in beams has attracted much attention from researchers, due to its greater complexity compared to single crack identification [5].
Modal curvature is a more advanced dynamic feature that can be used for identifying multiple damage in beams compared to other dynamic characteristics. Modal curvature was first proposed by Pandey [6], and its applications to the detection of single damage can be found extensively. Typical cases of the use of modal curvatures to identify multiple damage are as follows. Dawari and Vesmawala [7] employed the difference of modal curvatures for pairs of mode shapes of damaged and intact beams to identify double cracks. The method was numerically validated in the case of a reinforced concrete beam with multiple honeycomb damage. Wahab and De Roeck [8] identified multiple faults in a continuous beam using the averaged difference of modal curvatures for pairs of mode shapes of damaged and intact states. The technique successfully identified the locations of settlement damage in a concrete bridge. Sung et al. [9] explored the normalized curvature of a uniform load surface to reveal multiple damage in beam-like structures. Numerical results showed that the proposed method accurately located multiple damage. Despite the prevalence of its use in detecting multiple damage, modal curvature has a noticeable drawback of susceptibility to noise [10-14]. This deficiency usually produces a noisy modal curvature with the damage signature obscured, likely frustrating identification of the damage. To reveal actual multiple damage features by suppressing noise interference, Cao et al. [13, 14] proposed an alternative real-wavelet modal curvature. This quantity features effective suppression of noise but the concomitant occurrence of blunting of the singularity peak for damage – not an optimal solution for the characterization of multiple damage. To further advance the applicability of real-wavelet modal curvature, a new concept of complex-wavelet modal curvature is proposed in this study. This new concept features the prominent capability of detecting multiple damage in noisy environments.
The rest of the paper is organized as follows. Section 2 briefly describes the general principle of modal curvature for damage detection in beams. Section 3 formulates a new concept of complex-wavelet modal curvature. Section 4 experimentally validates the ability of the complex-wavelet modal curvature to detect multiple cracks in a composite beam with its mode shapes acquired by a scanning laser vibrometer (SLV). Conclusions are given in Section 5.
2. Principle of modal curvature in portraying damage
Modal curvature of a beam is defined by the second order derivative of the mode shape of the beam [6]:
where is the bending moment, is the bending stiffness, and and (the prime denotes the differentiation) are the mode shape and the modal curvature of the beam, respectively. is approximately obtained by the second-order central difference of with the sampling interval . Damage can change , causing discontinuity in ; contrariwise, discontinuity recognized in is likely to manifest the presence, location, and even extent of the damage. The modal curvature is thus an ideal dynamic feature in the theoretical foundation of damage indication [6]. Unfortunately, modal curvature obtained from densely-measured mode shape is prone to measurement noise, due to the fact that any slight noise involved in mode shapes may be considerably amplified by the second-order differentiation in Eq. (1) [10-14].
3. Complex-wavelet modal curvature
3.1. Complex wavelet transform
To satisfy the demands of damage characterization, a dedicated complex wavelet is derived from the second-order derivative of Gabor wavelet. Starting with the mother Gabor wavelet [15, 16] of non-zero mean at low oscillation with [17], its second-order derivative is:
where is normalized Gaussian function. satisfies the admissibility condition of a wavelet [18]:
where is the Fourier counterpart of via Fourier transform. Therefore, is qualified to function as a continuous complex wavelet. The real and imaginary parts of can be written with trigonometric functions:
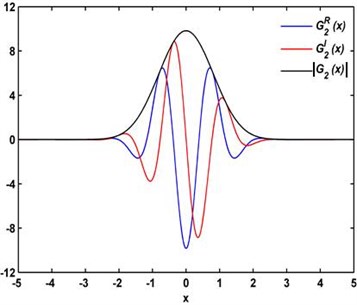
By way of illustration, Fig. 1 shows , , and the modulus of with .
Fig. 1Real part G2R(x), imaginary part G2I(x), and modulus G2(x) of the complex wavelet G2(x) with σ2=1/2 and η=3
The wavelet transform using wavelet can be expressed as [18]:
where is called the wavelet transform coefficient of ; ; denotes the complex conjugate of ; denotes the convolution of with , with being the notation of convolution.
3.2. Complex-wavelet modal curvature
A new concept of complex-wavelet modal curvature is formulated, based on the relation of being the second-order derivative of , as described in Eq. (2), and the differential property of convolution :
where indicates that the convolution of with produces a new modulus of modal curvature, , termed a complex-wavelet modal curvature.
In what follows, and are selected to specify the complex wavelet used for damage detection. The modulus of complex-wavelet modal curvature, , for the th mode shape is denoted as , with being the order of mode of .
4. Experimental validation
The applicability of the proposed complex-wavelet modal curvature to identify multiple damage is experimentally validated in a carbon-fiber-reinforced polymer (CFRP) composite beam with three cracks.
4.1. Set-up
A CFRP beam of length of 500 mm, width 10 mm, and depth 1.5 mm, consisting of five layers with each layer 0.3 mm in thickness, is taken as the experimental sample. Geometrical dimensions of the beam are shown in Fig. 2 in millimeters. As shown in Fig. 2, the beam is clamped at the left end with the fixing area spanning 10 mm from the left edge. Three cracks are initially made by cutting into the beam with a knife to produce three cuts about 0.5 mm in width. The first two cuts are of 0.3-0.6 mm in depth between the first and the second layers, and the third cut is of 0.3-0.6 mm in depth in the first layer. The first, second, and third through-width cracks, labeled by dashed lines in Fig. 2, occur at locations 113 mm, 221 mm, and 365 mm from the left edge, respectively.
Fig. 2Dimensions in millimeters of cracked beam with exciter and measurement points
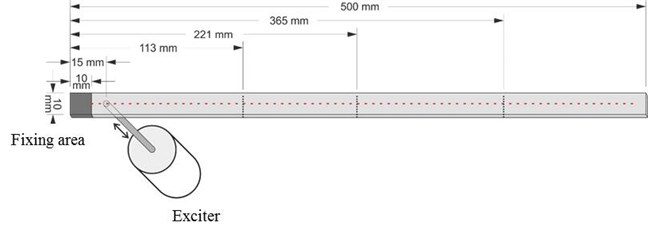
A vibration exciter (B&K® 4809), attached to the damaged side of the beam, 15 mm from its left edge, acts as an actuator to excite the beam. When the beam vibrates under harmonic excitation, a SLV is used as a sensor to scan the intact side of the beam to acquire the velocity response shape. The SLV (Polytec PSV-400) scans over 499 measurement points uniformly distributed on the intact surface, 10 mm through 496 mm from the left edge; the dimensionless locations for the first, second, and third cracks are , , and , respectively.
4.2. Results
The beam is excited under the fourth natural frequency to obtain the fourth mode shape for illustration of damage identification. When the beam vibrates, the SLV is used to measure the mode shape.
From the measured fourth mode shape, the modal curvature , obtained by Eq. (1), is shown in Fig. 3. In this figure, intense noise considerably obscures the damage signatures of modal curvatures. Thus, susceptibility to noise severely hampers the ability of conventional modal curvature to characterize multiple damage in noisy conditions.
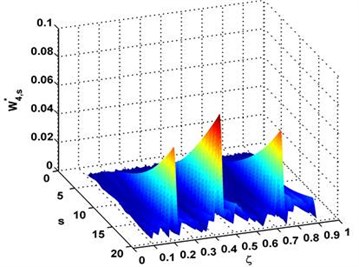
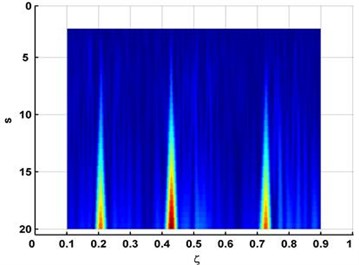
From the measured fourth mode shape, the complex-wavelet modal curvature , obtained by Eq. (6), is shown in Fig. 4. Three peaks stand out dominantly in (Fig. 4(a)) with the peak locations at , , and (Fig. 4(b), in good agreement with the actual locations of the first, second, and third cracks.
The experimental results show that the complex-wavelet modal curvature is more robust to noise and more sensitive to damage than conventional modal curvature.
Fig. 3Modal curvature W4'' of the fourth mode shape
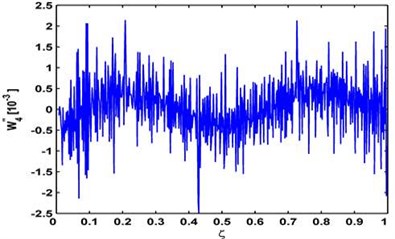
Fig. 4Complex-wavelet modal curvature a) and its planform b) for the fourth mode shape
a)
b)
5. Conclusions
This study presents a new dynamic feature, complex-wavelet modal curvature, for identification of multiple damage in noisy environments. The complex-wavelet modal curvature features robustness to measurement noise as well as sensitivity to damage. These prominent properties largely overcome the susceptibility of conventional modal curvature to noise in characterizing damage. The proposed complex-wavelet modal curvatures are experimentally validated in cases of beams with multiple cracks. The results show that the complex-wavelet modal curvature can identify and locate multiple damage in beams in noisy environments. Some observations are as follows:
1) The complex-wavelet modal curvature retains the physical propensity of modal curvature for revealing damage.
2) Compared with modal curvature, the complex-wavelet modal curvature is capable of alleviating noise effects at large scales.
3) The complex-wavelet modal curvature exhibits obvious advantages for characterizing damage in noisy environments, namely absence of the requirement for a baseline, damage sensitivity, and robustness against measurement noise.
References
-
Wang Q., Deng X. M. Damage detection with spatial wavelets. International Journal of Solids and Structures, Vol. 36, Issue 23, 1999, p. 3443-3468.
-
Wang S. S., Ren Q. W., Qiao P. Z. Structural damage detection using local damage factor. Journal of Vibration and Control, Vol. 12, Issue 9, 2006, p. 955-973.
-
Farrar C. R., Worden K. An introduction to structural health monitoring. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, Vol. 365, 2007, p. 303-315.
-
An Y. H., Ou J. P. Experimental and numerical studies on model updating method of damage severity identification utilizing four cost functions. Structural Control and Health Monitoring, Vol. 20, Issue 1, 2013, p. 107-120.
-
Sekhar A. S. Multiple cracks effects and identification. Mechanical Systems and Signal Processing, Vol. 22, Issue 4, 2008, p. 845-878.
-
Pandey A. K., Biswas M., Samman M. M. Damage detection from changes in curvature mode shapes. Journal of Sound and Vibration, Vol. 145, Issue 2, 1991, p. 321-332.
-
Dawari V. B., Vesmawala G. R. Modal curvature and modal flexibility methods for honeycomb identification in reinforced concrete beams. Procedia Engineering, Vol. 51, 2013, p. 119-124.
-
Wahab M. M. A., De Roeck G. Damage detection in bridges using modal curvatures: application to a real damage scenario. Journal of Sound and Vibration, Vol. 226, Issue 2, 1999, p. 217-235.
-
Sung S. H., Jung H. J., Jung H. Y. Damage detection for beam-like structures using the normalized curvature of a uniform load surface. Journal of Sound and Vibration, Vol. 332, Issue 6, p. 1501-1519.
-
Cao M. S., Qiao P. Z. Novel Laplacian scheme and multiresolution modal curvatures for structural damage identification. Mechanical Systems and Signal Processing, Vol. 23, Issue 4, 2009, p. 1223-1242.
-
Cao M. S., Cheng L., Su Z. Q., Xu H. A multi-scale pseudo-force model in wavelet domain for identification of damage in structural components. Mechanical Systems and Signal Processing, Vol. 28, 2012, p. 638-659.
-
Cao M. S., Su Z. Q., Cheng L., Xu H. A multi-scale pseudo-force model for characterization of damage in beam components with unknown material and structural parameters. Journal of Sound and Vibration, Vol. 332, Issue 21, 2013, p. 5566-5583.
-
Cao M. S., Xu W., Ostachowicz W., Su Z. Q. Damage identification for beams in noisy conditions based on Teager energy operator-wavelet transform modal curvature. Journal of Sound and Vibration, Vol. 333, Issue 6, 2014, p. 1543-1553.
-
Cao M. S., Radzieński M., Xu W., Ostachowicz W. Identification of multiple damage in beams based on robust curvature mode shapes. Mechanical Systems and Signal Processing, Vol. 46, Issue 2, 2014, p. 468-480.
-
Crossmann A., Morlet J. Decomposition of hardy functions into square integrable wavelets of constant shape. SIAM Journal on Mathematical Analysis, Vol. 15, Issue 4, p. 723-736.
-
Daubechies I. The wavelet transform, time-frequency localization and signal analysis. IEEE Transactions on Information Theory, Vol. 36, Issue 5, p. 961-1005.
-
Addison P. S., Watson J. N., Feng T. Low-oscillation complex wavelets. Journal of Sound and Vibration, Vol. 254, Issue 4, p. 733-762.
-
Mallat S. A Wavelet Tour of Signal Processing. Third Edition. Academic Press, San Diego, 2008.
About this article
The authors are grateful for the partial support provided by the Natural Science Foundations of China (No. 11172091), Qing Lan Project, and the Fundamental Research Funds for the Central Universities (Grant Nos. 2014B03914 and 2012B05814).
