Abstract
Modal curvatures are widely used in damage detection in beams and plates, allowing not only indication of damage occurrence but also determination of damage location, with no need for prior knowledge of the structure being inspected. Notably, however, modal curvatures have an intrinsic deficiency of susceptibility to noise involved in measurement, the noise effect easily masking genuine damage feature in the modal curvature. To overcome this deficiency, a new philosophy of adopting wavelet transform theory to create wavelet modal curvatures is formulated, from which a series of new concepts are derived, including 1D wavelet modal curvature, 2D wavelet modal curvature, and complex wavelet modal curvature. The multiscale property of wavelets endows these newly developed modal curvatures with the predominant characteristics of robustness against noise together with intensification of slight damage. A set of experimental cases is provided to demonstrate the capability of wavelet modal curvatures to identify complex damage in aluminum and composite structures.
1. Introduction
Structural health monitoring and damage detection relying on vibration characteristics has been a research focus of increasing interest in various fields such as mechanical, civil, aerospace, and military, during the last few decades [1-2]. Among methods for vibration-based damage detection, modal curvature is a representative damage feature with frequently mentioned merits: (i) accurate indication of damage occurrence; (ii) instant determination of damage location, and (iii) no need for prior knowledge of damage. 1D and 2D modal curvatures have been widely applied to the identification of damage in beams [3-8] and plates [9-13] in relatively high signal-to-noise ratio (SNR) conditions. Despite its prevalence in portraying damage, modal curvature has the notable deficiency of susceptibility to measurement noise: when modal curvature is derived by second-order differentiation of a mode shape, the measurement noise involved in the mode shape can be considerably amplified by the differentiation, likely obscuring genuine damage characteristics and so frustrating damage identification. Some researchers [7-8] have devised strategies with the aim of overcoming this deficiency of modal curvature. Nevertheless, the majority of the developed methods rely on denoising, optimizing sampling interval, etc., without being able to solve the problem with solid theoretical and physical support. To address this problem, the group the author works in reforms the conventional modal curvature using wavelet transform techniques, producing a novel type of wavelet modal curvatures. Wavelet modal curvature enjoys the multiscale property of the wavelet transform in adaptability to noise, exhibiting distinctive advantages of robustness against noise in characterizing damage. In this study, wavelet modal curvatures developed in our group are briefly introduced and their capabilities to identify damage in noisy environments are demonstrated in experimental cases.
2. Conventional modal curvature
The modal curvature of a vibrating beam is defined by the second-order derivatives of a mode shape [3]:
where is the bending moment and is the flexural stiffness.
The modal curvature of a vibrating thin plate is defined by the 2D Laplacian of a mode shape :
where is the flexural rigidity with the Young’s modulus, the Poisson’s ratio, and the thickness of the plate; and are bending moments in the and directions.
Damage causes change in for beams or for plates. The change entails discontinuity in or under the premise of continuity in bending moment. Discontinuity in the modal curvature manifests the occurrence, location, and even severity of damage. This theoretical observation lays the foundation for using modal curvature to identify damage.
The Fourier counterparts of modal curvatures, and are and respectively, where represents the angular frequency. The square of , or in the Fourier counterpart necessarily enlarges the high-frequency contents in mode shapes. Owing to the fact that measurement noise is commonly of predominantly high-frequency components, these components are thereby favorably enlarged such that they likely dominate the modal curvature [7, 14].
3. Wavelet modal curvature
Wavelet modal curvature is formulated based on using a wavelet transform to expand a modal shape from a space domain to a space-scale domain [15], with accomplishment of the second-order differentiation function at the scale level.
1) 1D wavelet modal curvature: [16, 17]:
where denotes the manipulation of convolution; at the scale is derived from the mother wavelet ; is specified by the second-order derivatives of the smooth function , typically the Gaussian function, for which ; is the translation parameter.
2) 2D wavelet modal curvature: [17]:
where at the scale originates from the mother wavelet ; is defined by the second-order derivatives of the smooth function , for which ; and are the translation parameters in the and directions, respectively.
In Eqs. (3) and (4), or is generated by second-order differentiation of a beam mode shape or a plate mode shape that is pre-smoothed by and , respectively. The wavelet modal curvature inherits from the wavelet transform the multiscale property, which provides a distinctive mechanism of adaptability to noise [15-17].
For post-processing, the Teager energy operator (TEO), , is generally employed to further treat the wavelet modal curvature with the aim of intensifying damage features [18, 19]:
where is the 1D TEO-processed wavelet modal curvature for a beam and is the 2D TEO-processed wavelet modal curvature for a plate.
3) Complex-wavelet modal curvature: [20]:
A complex-wavelet modal curvature features both noise robustness and damage sensitivity [20], defined by:
where at the scale is derived from the complex mother wavelet ; is set by the second-order differentiation of the smooth complex function , for which ; is the translation parameter. The complex-wavelet modal curvature consists of a pair of real and imaginary parts, their modulus designating damage.
4. Experimental validation
4.1. Wavelet modal curvature
1) for detecting multiple cracks in aluminum beams.
An aluminum beam with three cracks is excited by an electromechanical shaker (Fig. 1) and its mode shapes are acquired by a scanning laser vibrometer (SLV) [21]. As illustrated by the 5th mode shape, the relevant 1D TEO-processed wavelet modal curvature is dominated by three singular peaks increasing with scale, and they clearly pinpoint the actual cracks (Fig. 2).
Fig. 1Alunimun beam with three cracks [17]
![Alunimun beam with three cracks [17]](https://static-01.extrica.com/articles/15608/15608-img1.jpg)
Fig. 21D TEO-processed Ws*(u) [17]
![1D TEO-processed Ws*(u) [17]](https://static-01.extrica.com/articles/15608/15608-img2.jpg)
2) for identifying multiple cracks in composite beams.
A carbon-fiber-reinforced polymer (CFRP) composite beam consisting of five layers is considered, in which three cracks are cut deep into the second layer (Fig. 3). An electromechanical shaker is used to excite the beam together with its mode shapes measured by a SLV. The 4th mode shape is arbitrarily selected to exemplify the method. In the complex-wavelet modal curvature, three peaks arising along scale clearly designate the genuine cracks (Fig. 4).
Fig. 3CFRP beam with a crack [20]
![CFRP beam with a crack [20]](https://static-01.extrica.com/articles/15608/15608-img3.jpg)
Fig. 4Complex-wavelet modal curvature [20]
![Complex-wavelet modal curvature [20]](https://static-01.extrica.com/articles/15608/15608-img4.jpg)
3) for characterizing cross-like notch in aluminum plates.
An aluminum plate containing a cross-like notch, with its geometry shown in Fig. 5, is excited with a piezoelectric lead-zirconate-titanate (PZT) actuator. The mode shapes of the plate are obtained by using a SLV as a sensor. A distinct peak appearing in the 2D-TEO processed wavelet modal curvature (at scale 20) of the mode shape at the natural frequency of 3000 Hz clearly delineates the notch (Fig. 6).
Fig. 5Aluminum plate with a cross-like notch: a) geometry and b) zoomed-in notch [17]
![Aluminum plate with a cross-like notch: a) geometry and b) zoomed-in notch [17]](https://static-01.extrica.com/articles/15608/15608-img5.jpg)
Fig. 62D-TEO processed wavelet modal curvature: a) planform and b) enlarged damage [17]
![2D-TEO processed wavelet modal curvature: a) planform and b) enlarged damage [17]](https://static-01.extrica.com/articles/15608/15608-img6.jpg)
4.2. Conventional modal curvature
The experimental cases above are reanalyzed by conventional modal curvatures, with the results shown in Figs. 7(a), 7(b), 7(c) for the aluminum beam, composite beam, aluminum plate, respectively. In these modal curvatures, the noise effect entirely impairs the modal curvatures, from which no damage feature is identifiable. Comparisons with the results from wavelet modal curvatures in Figs. 2, 4, 6 clearly illustrate the disadvantage of conventional modal curvature in resisting noise.
Fig. 7Modal curvatures for: a) aluminum beam, b) composite beam, and c) aluminum plate
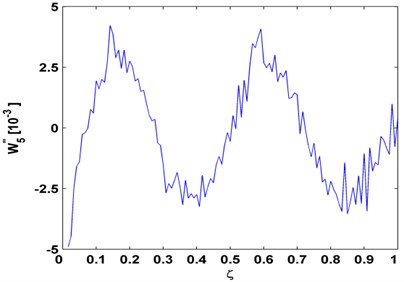
a)
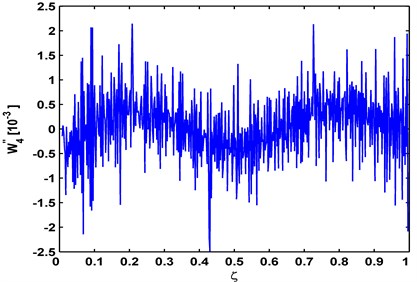
b)
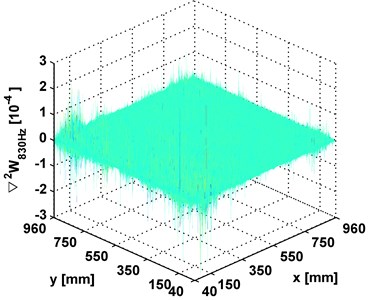
c)
5. Conclusions
Modal curvature is a widely used damage indicator with explicit physical implication; however, its noise susceptibility compromises its effectiveness in characterizing damage in noisy conditions. This study reports new concepts of wavelet modal curvatures that has superiority over conventional modal curvature in the mechanism of adaptability to noise. The capabilities of wavelet modal curvatures to detect complex damage in noisy environments are demonstrated in experimental cases.
References
-
Doebling S. W., Farrar C. R., Prime M. B., Shevitz D. W. Damage identification and health monitoring of structural and mechanical systems from changes in their characteristics: A literature review, Los Alamos National Lab., United States, 1996.
-
Ou J. P., Li H. Structural health monitoring in mainland China: review and future trends. Structural Health Monitoring, Vol. 9, Issue 3, 2010, p. 219-231.
-
Pandey A. K., Biswas M., Samman M. M. Damage detection from changes in curvature mode shapes. Journal of Sound and Vibration, Vol. 145, Issue 1991, p. 321-332.
-
Abdel Mahab M. M., De Roeck G. Damage detection in bridges using modal curvatures: application to a real crack scenario. Journal of Sound and Vibration, Vol. 226, Issue 2, 1999, p. 217-235.
-
Whalen T. M. The behavior of higher order mode shape derivatives in damaged, beam-like structures. Journal of Sound and Vibration, Vol. 309, Issue 3-5, p. 2008, p. 426-464.
-
Roy K., Ray-Chaudhuri S. Fundamental mode shape and its derivatives in structural damage localization. Journal of Sound and Vibration, Vol. 332, Issue 21, 2013, p. 5584-5593.
-
Cao M. S., Qiao P. Z. Novel Laplacian scheme and multisolution modal curvatures for structural damage identification. Mechanical Systems and Signal Processing, Vol. 29, 2009, p. 638-659.
-
Sazonov E., Klinkhachorn P. Optimal spatial sampling interval for damage detection by curvature or strain energy mode shapes. Journal of Sound and Vibration, Vol. 285, 2005, p. 783-801.
-
Qiao P. Z., Lu K., Lestari W., Wang J. L. CMS-based damage detection in composite laminated plates. Composite Structures, Vol. 80, 2007, p. 409-428.
-
Li Y. Y., Cheng L., Yam L. H., Wong W. O. Identification of damage locations for plate-like structures using damage sensitive indices: strain modal approach. Computers and Structures, Vol. 80, 2002, p. 1881-1894.
-
Hu N., Fukunaga H., Kameyama M., Aramaki Y., Change F. K. Vibration analysis of a delaminated composite beams and plates using a high-order finite element. International Journal of Mechanical Sciences, Vol. 44, 2002, p. 1479-1503.
-
Wu D., Law S. S. Damage localization in plate structures from uniform load surface curvature. Journal of Sound and Vibration, Vol. 276, 2004, p. 227-244.
-
Yoon M. K., Heider D., Gillespie Jr. J. W., Ratcliffe C.P., Crane R. M. Local damage detection using the two-dimensional gapped smoothing method. Journal of Sound and Vibration, Vol. 279, 2005, p. 119-139.
-
Xu W., Cao M. S., Ostachowicz W., Radzieński M., Xia N. 2D Curvature mode shape based on wavelets and Teager energy for damage detection in plates. Submitted to Journal of Sound and Vibration.
-
Mallat S. A Wavelet Tour of Signal Processing, Third Edition. Academic Press, San Diego, 2008.
-
Cao M. S., Xu W., Ostachowicz W., Su Z. Q. Damage identification for beams in noisy conditions based on Teager energy operator-wavelet transform modal curvature. Journal of Sound and Vibration, Vol. 333, Issue 6, 2014, p. 1543-1553.
-
Cao M. S., Radzieński M., Xu W., Ostachowicz W. Identification of multiple damage in beams on robust curvature mode shapes. Mechanical Systems and Signal Processing, Vol. 46, 2014, p. 468-480.
-
Teager H. M., Teager S. M. A phenomenological model for vowel production in the vocal tract. College-Hill Press, San Diego, 1983.
-
Kaiser J. F. On a simple algorithm to calculate the energy of a signal. International Conference on Acoustics, Speech, and Signal Processing, 1990, p. 381-384.
-
Xu W., Radzieński M., Ostachowicz W., Cao M. S. Detection of multiple damage in beams based on complex-wavelet modal curvature. Submitted to Structural Health Monitoring.
-
Xu W., Radzieński M., Ostachowicz W., Cao M. S. Damage detection in plates using two-dimensional directional Gaussian wavelets and laser scanned operating deflection shapes. Structural Health Monitoring, Vol. 12, Issue 5-6, 2013, p. 457-468.
About this article
The author gratefully acknowledges the Fundamental Research Funds for the Central Universities (Grant Nos. 2014B03914 and 2012B05814) and Natural Science Foundation of China (Grant No. 11172091) for the financial support for this study.
