Abstract
Aiming at the problem of noise during the operation of the pyrotechnic separation device, this paper uses LS-DYNA software to simulate the separation process of the separation nut. Then uses the LMS Virtual.Lab software to predict and analyse the mechanical impact noise during the separation, and quantitatively decoupling the contribution rate of the mechanical noise generated by the movement of each component. The results indicate that the inner sleeve impact is the main source of mechanical noise during the separation (more than 90 %).

Highlights
- The numerical simulation method of separation process and mechanical noise of separation nut was established.
- Two special numerical models were designed to quantitatively decouple the mechanical noise generated by each component.
- The main noise sources are identified.
1. Introduction
Pyrotechnic devices are widely used in the separation of payloads on spacecraft, the deployment of antennas, the release of solar panels, and the separation of loads on underwater vehicles [1-2]. However, in the application of underwater equipment, due to the different operating environment and underwater equipment characteristics, reducing the operation noise level has become a new requirement for pyrotechnic separation devices [3].
The noise in the separation process of the pyrotechnic separation device mainly comes from two aspects: (1) the combustion noise generated during the explosion of the internal gunpowder; (2) the mechanical noise generated by the movement and collision of the internal mechanism [4]. For the combustion noise generated by the explosion of the pyrotechnic composition, Xiong Shi-hui established a fluid-solid-acoustic one-way coupling calculation model for the combustion of energetic materials in a closed bomb [5], which provides guidance for the prediction of combustion noise. In the current research of pyrotechnic separation devices, the method of using LS-DYNA to simulate and analyze the separation process has been relatively mature [6-8]. In terms of mechanical impact noise, Li Ying-gang combined the acoustic theory and the finite element-transient boundary element method to simulate the impact noise [9], provides the method for the study of mechanical noise of pyrotechnical separation devices.
In this paper, a reverse push type pyrotechnical separation nut is used as the research object, and combining the finite element method and the transient boundary element method to study the mechanical noise during the separation of the pyrotechnic separation device. First, using LS-DYNA to establish the finite element model and simulate the entire separation process. Then import the finite element calculation result into LMS Virtual.Lab as an excitation, and use the transient boundary element method to calculate the transient radiation noise. In this way, the mechanical noise in the separation process is predicted and quantitatively decoupled to clarify the main noise sources and provide guidance for the noise reduction design research of the pyrotechnical separation device.
2. Finite element model
2.1. Working principle and the finite model establishment
The structure of the studied separation nut is shown in Fig. 1. Before action, due to the limiting effect of the shear pin, the inner sleeve can maintain the radial constraint of the threaded segment. When unlocked, the pyrotechnic composition acts in the electric explosive chamber (not shown) to produce high-temperature and high-pressure gas products, which pass through the orifice to the inner cavity of the piston. When the pressure in the cavity reaches the critical starting pressure, the inner sleeve cuts the shear pin and moves to the left; when the inner sleeve moves to a certain stroke, the restriction of the threaded segment is released, and starts to expand radially under the push of the piston and the tension of the preloading, and the restraint of the connecting bolts is released.
Fig. 1Reverse push-type separation nut structure. 1. – housing, 2 – cushion, 3 – seal ring, 4 – shear pin, 5 – piston, 6 – inner sleeve, 7 – threaded segment, 8 – bolt, 9 – end cover, 10 – mounting block, 11 – response plate
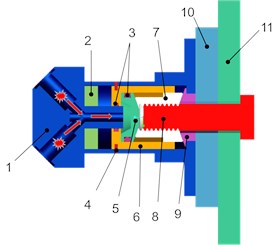
a) Before action
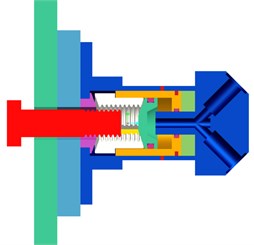
b) After action
Analysis of the separation process of the separation nut shows that the mechanical noise may originate from three aspects:
1) Fracture of the shear pin;
2) Impact when the inner sleeve moves in place;
3) Impact during the movement of the threaded segment.
The 1/2 finite element model is established based on the separated nut structure, and the final model is shown in Fig. 2. To simplify the model, components such as electric blast tube, sealing ring and some features that have no major influence on the calculation results are deleted.
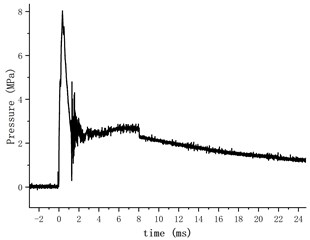
The material model parameters reference the document [10]. The pressure-time curve of the gas in the cavity is applied to the inner sleeve and the piston to replace the burning of gunpowder and realize the motion simulation analysis of the internal mechanism. The test of the pressure time history curve is shown in Fig. 3.
Fig. 2Separation nut 1/2 finite element model
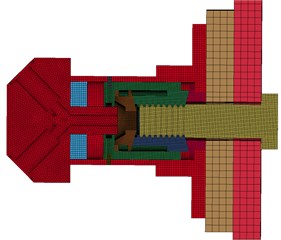
Fig. 3Pressure loading curve
2.2. Simulation results analysis
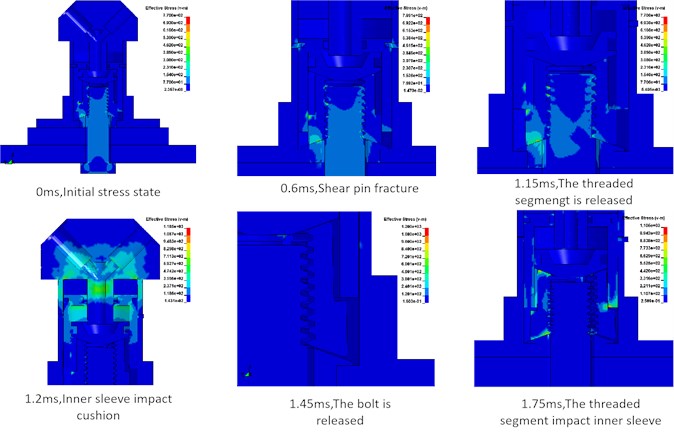
In order to analyze the stress state of the components in the separation process of the separation nut, the Von-Mises stress nephogram at several critical moments in the separation process are extracted, as shown in Fig. 4. At 0.6 ms, the shear pin is sheared, and the inner sleeve starts to accelerate. At 1.15 ms, the inner sleeve reaches the unlocking stroke, which releases the restriction of the threaded segment, and the threaded segment begin to move radially. At 1.2 ms, the inner sleeve moves to the maximum stroke, and hitting the cushion. At 1.45 ms, the threaded segment releases the restraint on the connecting bolt to realizes separation. At 1.75 ms, the threaded segment moves to the maximum stroke and hits the inner sleeve.
Fig. 4Stress nephogram at several critical moments during the separation process
3. Radiation noise calculation
3.1. Boundary element model
In this paper, the boundary element method in the LMS Virtual.Lab software is used to simulate the transient mechanical noise during the separation process. The boundary element numerical calculation model is shown in Fig. 5. The structural mesh is imported directly from the Hypermesh software, and the boundary element mesh and the field point grid are generated directly in the LMS Virtual.Lab. Compared with the separation nut, the acoustic radiation area of the response plate is larger and has a greater impact on the noise results. Therefore, in order to analyze the acoustic radiation characteristics of the separation nut itself, the response plate is regarded as an infinite baffle and is not considered when calculating the radiated noise, that is, the boundary element mesh only includes the surface mesh of the separated nut , which is divided by triangular elements. The grid size of the field points is 2 mm, and the monitoring points are distributed on a circumference with the origin as the center and a radius of 0.5 m.
3.2. Simulation results analysis
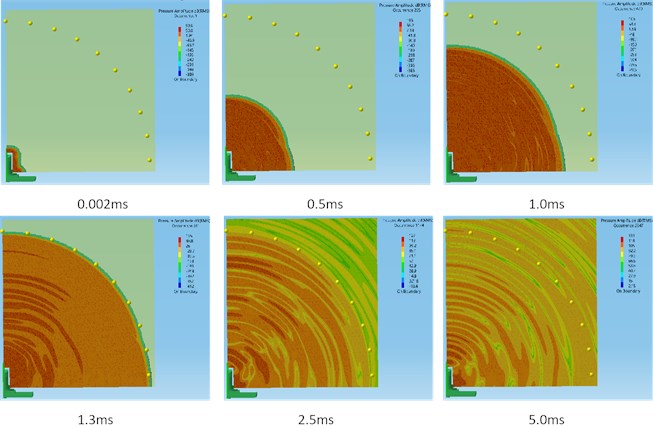
Import the vibration displacement results calculated by LS-DYNA into LMS Virtual.Lab as the excitation of the acoustic response and to realize the visualization of the acoustic radiated. The propagation process for transient radiated sound wave is shown in Fig. 6.
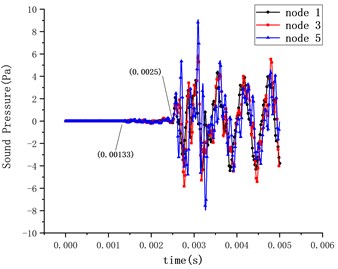
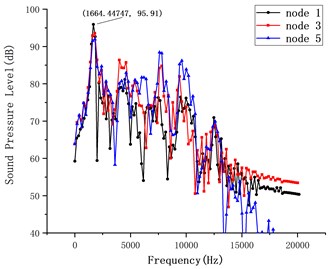
The radiation noise data at the three monitoring points of 1#, 3# and 5# located on the same circle with distribution angles of 0°, 20° and 40° were compared, as shown in Fig. 7.
Fig. 5Transient acoustic boundary element model
Comparing Fig. 7 (a) and Fig. 4, the noise signal is transmitted to the monitoring point at 1.3 ms, the sound pressure at the monitoring point begins to fluctuate slightly, which corresponds to the movement process before the inner sleeve hits the cushion. At 2.5 ms, the radiation sound pressure at the monitoring point began to fluctuate greatly, corresponding to the time when the inner sleeve hits the cushion.
In Fig. 7(b), the radiated noise generated by mechanical collision during the separation of the separation nut is mainly concentrated in the low-frequency region of 10-5000 Hz, and there is a peak sound pressure level at 1664 Hz. Within this frequency range, the sound pressure level curve of the three monitoring points is basically consistent, showing weak radiation directivity characteristics. Combined with the above analysis, the radiated sound wave can be regarded as a hemispherical wave. In the subsequent analysis, the data of the 1# monitoring point is used as an example for analysis.
Fig. 6The propagation process for transient radiated sound wave
3.3. Noise sources simulation decoupling analysis
Due to the rapid separation process, it is difficult to separate the noise generated by the impact of the inner sleeve, the fracture of the shear pin and the impact of the threaded segment through the time-domain sound pressure curve. In order to analyze their respective contributions to the total mechanical noise, two special numerical models are designed.
Fig. 7Comparison of radiation noise results at different monitoring points
a) Transient sound pressure curve
b) Sound pressure level spectral curve
1) Only the shear pin fracture model (Model Ⅰ).
In this model, it is calculated until the shear pin breaks and the inner sleeve does not reach the unlocking stroke. It is considered that the radiation noise is only caused by the fracture of the shear pin.
2) Isolation inner sleeve impact model (Model Ⅱ).
In this model, before the inner sleeve hits the cushion, the movement of the inner sleeve is restricted. Since the inner sleeve has already moved to the end of the stroke at this time, this action will not affect the entire separation process. It is believed that this noise result is mainly caused by the impact of the threaded segment and the fracture of the shear pin.
Regarding the noise generated by the movement of each component during the separation process as independent sound sources that exist at the same time, the superposition principle of sound pressure level can be used to separate the independent sound sources:
According to the analysis in 3.2, the radiated sound wave generated by mechanical collision during the separation of the separation nut is hemispherical surface wave. The conversion formula between sound power and sound pressure level is as follows:
In above, is the sound pressure level (dB); is the sound pressure level of independent sound source(dB); is the sound power level (dB); is the sound radiation area (m2); is the distance of the monitoring point from the sound source (m); is the total sound power (W); is the sound power of independent sound source (W); is the contribution rate; is the benchmark sound power, and its value is 1×10-12 W in air.
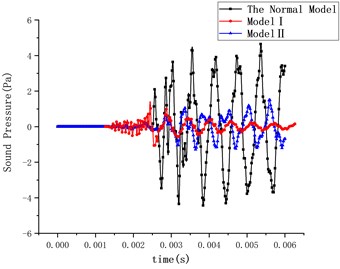
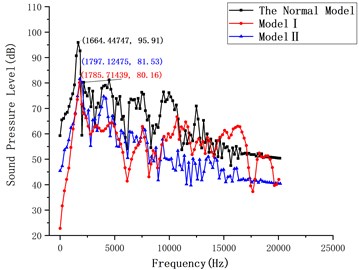
The noise results calculated by the two models compare with the original model as shown in Fig. 8.
Eqs. (1), (2) is used to calculate the band sound pressure level in the frequency range of 10-5000 Hz for different models and decouple the mechanical noise in the separation process, then convert it to sound power and calculate the contribution rate of mechanical noise generated by the independent movement of each component, as shown in Table 1. The results show that the mechanical noise in the separation process of separating nut mainly comes from the impact of inner sleeve, and the fracture of shear pin and the impact of nut flap have little effect on the noise results.
Fig. 8Comparison of radiation noise results in different models
a) Transient sound pressure curve
b) Sound pressure level spectral curve
Table 1Band sound pressure level and the contribution rate of each noise source
Whole-process | Shear Pin fracture | The impact of the Inner Sleeve | The impact of the Threaded Segment | |
Band sound pressure level (dB) | 98.98 | 82.56 | 98.76 | 83.42 |
Sound power (W) | 0.0125 | 2.84e-4 | 0.0119 | 3.47e-4 |
The contribution rate | 100 % | 2.3 % | 94.9 % | 2.8 % |
4. Conclusions
In this work, the finite element model of a reverse push type pyrotechnical separation nut is established and calculated by LS-DYNA. It is considered that the mechanical noise in the separation process mainly comes from three aspects: shear pin fracture, the impact of the inner sleeve and the impact of the threaded segment impact. Based on the simulation results of the finite element model, combined with the transient boundary element method, the mechanical collision noise generated in the separation process is simulated and predicted by using the LMS virtual. Lab acoustic module.
By designing a few individual finite element models, and the different sources of mechanical noise in the separation process are decoupled by using the superposition principle of sound pressure level. The results show the radiation noise caused by the impact of the inner sleeve accounts for 94.9 % of the total radiation noise. The radiation noise caused by the impact of the threaded segment accounts for 2.8 % of the total. The radiation noise caused by the fracture of the shear pin accounts for 2.3 % of the total. Therefore, the mechanical noise generated in the separation process can be decreased by reducing the impact of the inner sleeve.
References
-
Bement L. J. and Schimmel M. L., “A manual for pyrotechnic design, development and qualification,” Hampton NASA, 1998.
-
Gao Bin, “Application of pyrotechnically actuated devices,” Spacecraft Recovery and Remote Sensing, Vol. 1, pp. 55–59, 2004.
-
Xu San-Xiang, “The development of self-guided sea mine and self-guide device,” Ship Science and Technology, Vol. 2, pp. 89–91, 2008.
-
Chen Xia and Tian Rong-Yan, “Research on the charge weight and the sound source level of underwater separation of pyrotechnic separation device,” Ship Science and Technology, Vol. 34, No. 11, pp. 122–124, 2012.
-
S.-H. Xiong, T. Yang, Y.-J. Wu, J.-C. Wang, Y. Li, and Y.-Q. Wen, “Numerical simulation of radiated noise during combustion of energetic materials in a closed bomb,” Defence Technology, Vol. 2021, No. 9, May 2021, https://doi.org/10.1016/j.dt.2021.05.013
-
Wang Jun-Ping, Mao Yong-Jian, and Huang Han-Jun, “Numerical simulation for impulsively loading mechanism of a point pyrotechnic separation device,” Journal of Vibration and Shock, Vol. 32, No. 2, pp. 9–13, 2013.
-
H. Zhao, W. Liu, J. Ding, Y. Sun, X. Li, and Y. Liu, “Numerical study on separation shock characteristics of pyrotechnic separation nuts,” Acta Astronautica, Vol. 151, pp. 893–903, Oct. 2018, https://doi.org/10.1016/j.actaastro.2018.07.040
-
S. Xiong, Y. Li, Y. Ye, J. Wang, H. Mu, and Y. Wen, “Quantitatively decoupling the impact of preload and internal mechanism motion on pyrotechnic separation shock,” International Journal of Aeronautical and Space Sciences, Vol. 22, No. 5, pp. 1106–1117, Oct. 2021, https://doi.org/10.1007/s42405-021-00354-2
-
Li Ying-Gang et al., “Theoretical analysis and numerical simulation for impact noise due to collision of two cylinders,” Journal of Vibration and Shock, Vol. 33, No. 15, pp. 162–166, 2014.
-
Li Yan-Hua, “Shock prediction and control of typical point pyrotechnical separation devices,” Beijing Institute of Technology, Beijing, 2015.
